＜マンゴルトの明示公式＞

前回チェビシェブ関数の積分表示

   Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} ζ'(s)/ζ(s)・x^s/s ds

を求めました。今回は積分を実行し、マンゴルトの明示公式を導出します。

　f_x(s)＝ζ'(s)/ζ(s)・x^s/s

とおくと

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds＝－1/2πi・∫_C1 f_x(s)ds

となります。この複素積分を閉曲線C(c,T,R）

　C(c,T,R)＝C_{1[c－Ti、c＋Ti]}＋C_{2[c+Ti、－R＋Ti]}＋C_{3[－R＋Ti、－R －Ti]}＋C_{4[－R－Ti、c－Ti]}

に拡張すると、

　lim_[R,T→∞]∫_C2 f_x(s)ds＝lim_[R,T→∞]∫_C3 f_x(s)ds＝lim_[R,T→∞]∫_C4 f_x(s)ds＝0

となるので、

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds

　　　　＝－1/2πi・lim_[R,T→∞]∫_C(c,T,R）f_x(s)ds

となります。閉曲線内に含まれるf_x(s)の極の留数を計算すれば、Ψ^*(x)を求めることができます。

＜マンゴルトの明示公式＞

チェビシェフの素数pの階段関数

　Ψ^*(x)＝Σ[n≦x]Λ(n)＝Σ[p^m≦x] log(p)

に関して

　Ψ^*(x)＝x－1/2・log(1－x^－2)－log 2π－Σ’_ρ∊Z0x^ρ/ρ

がなりたつ。ここでZ₀＝｛ｓ｜ζ(s)＝0なる非自明な零点｝である。マンゴルトの明示公式は、素数の分布を表す階段関数Ψ^*(x)がゼ－タ関数の非自明な零点の和を含むｘの解析関数によって書かれているという不思議な公式です。

閉曲線内の

　f_x(s)＝ζ'(s)/ζ(s)・x^s/s

の零点は、ρ＝1、－2n、0、ρ_iの4種類あります。

まずζ'(s)/ζ(s)の留数を考えます。

　ζ(s)～1/(s－1)+・・

　ζ'(s)～－1/(s－1)²+・・

　ζ'(s)/ζ(s)～－1/(s－1)+・・

なので、極をρとすると、位数Ord(ζ,ρ)について

　Res(ζ’/ζ,ρ)＝Ord(ζ,ρ)

が成り立ちます。偏角の原理より、留数は

　Res(ζ'(s)/ζ(s)・x^s/s,ρ)＝Ord(ζ,ρ) x^ρ/ρ

となります。

1）s＝1の留数

　Ord(ζ,1)＝－1となります。

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝1)＝Ord(ζ,1) x¹/1＝－x

2）s＝－2nの留数

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝－2n)＝Ord(ζ,1) x^－2n/(－2n)

R→∞でN→∞となるので

　－lim_[N→∞]Σ_n＝1～N x^－2n/(－2n)＝1/2・log(1－x^－2)

3）s＝0の留数

　　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝0)＝ζ'(0)/ζ(0)＝log(2π)

　　ζ(0)＝－1/2、ζ’(0)＝－1/2・log(2π)

4）ｓの非自明な零点ρ_iの留数

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝ρ_i)＝Ord(ζ,ρ_i) x^ρi /ρ_i

T→∞でN→∞となるので

　lim_[N→∞]Σ_i＝1～N Ord(ζ,ρ_i) x^ρi /ρ_i＝Σ’_ρ∊Z0 x^ρ /ρ

Σ’_ρ∊Z0は非自明な零点ρでの位数がｍの場合ｍ回和をとると言う意味です。

以上から、マンゴルトの明示公式

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds

　　　　＝－1/2πi・lim_[R,T→∞]∫_C(c,T,R）f_x(s)ds

　　　　＝－1/2πi・2πi・（－x＋1/2・log(1－x^－2)＋log 2π＋Σ’_ρ∊Z0 x^ρ /ρ）

　　　＝x－1/2・log(1－x^－2)－log 2π－Σ’_ρ∊Z0 x^ρ /ρ

が成り立ちます。

偏角原理とは、z=z₀でm位の特異点をもちそれ以外で正則な関数f(z)に関して

　Res(f’/f,z₀)＝Ord(f,z₀)＝m

が成り立つ定理です。f(z)は、z=z₀で特異点をもたない正則関数g(z)を用いて

　f(z)＝(z－z₀)^m・g(z)

と書けます。このとき、

　f'(z) /f(z)＝[m(z－z₀)^m－1・g(z)＋(z－z₀)^m・g'(z)]/ (z－z₀)^m・g(z)

　　　　　＝m/(z－z₀)＋g'(z)/ g(z)

なので、f'(z) /f(z)はz＝z₀で1位の極を持つことがわかり

　Res(f’/f,z₀) ＝m＝Ord(f,z₀)

が成り立ちます。

＜マンゴルト関数Λ(n)とチェビシェフ関数Ψ(x)＞

自然数nに対して、マンゴルト関数Λ(n)を

　　Λ(n)＝log(p)　if　n＝p^m, 　otherwise 0

と定義します。ここでpは素数です。具体的には

　Λ(1)＝0、Λ(2)＝log2、Λ(3)＝log3、Λ(4)＝Λ(2²)＝log2、Λ(5)＝log5、

　Λ(6)＝Λ(2・3)＝0、Λ(7)＝log7、Λ(8)＝Λ(2³)＝log2、Λ(9)＝Λ(3²)＝log3、

　Λ(10)＝Λ(2・5)＝0、Λ(11)＝log11、Λ(12)＝Λ(2・2・3)＝0、・・・

です。単一の素数のべき乗でのみΛ値がゼロではありません。

実数xに対して、チェビシェフ関数Ψ(x)を

　　Ψ(x)＝Σ_[n≦x]Λ(n)＝Σ_[p^m_≦x] log(p)

と定義します。ここでpは素数です。Σ_[p^m≦x]は、x以下の素数pの冪乗となっている素数pで和をとることを意味します。Ψ(x)は階段関数です。

ｘ＝5とすると

　　Ψ(5)＝Λ(1)＋Λ(2)＋Λ(3)＋Λ(4)＋Λ(5)＝0＋log2＋log3＋log2＋log5

となります。Ψ(x)のステップアップする点で、ステップアップ部分の中点をとる関数をΨ^*(x)と書きます。

　　Ψ^*(5)＝log2＋log3＋log2＋1/2・log5

となります。Ψ^*(x)では最後の項が1/2倍になります。ｘ＝9の場合は

　　Ψ(9)＝Λ(1)＋Λ(2)＋Λ(3)＋Λ(4)＋Λ(5)＋Λ(6)＋Λ(7)＋Λ(8)＋Λ(9)

　　　　＝0＋log2＋log3＋log2＋log5＋0＋log7＋log2＋log3

　　Ψ^*(9)＝log2＋log3＋log2＋log5＋log7＋log2＋1/2・log3

となります。ｘが素数のべき乗でない場合は、両関数は等しくなります。例えば

　　Ψ(1000)＝Ψ(997)＝Ψ^*(1000)

に注意して下さい。

ゼ－タ関数ζ(s)

・ζ(s)＝Σ_n＝1～∞ 1/n^s＝Π_p∊P [1－1/p^s]^－1

に関して、

　ζ'(s)/ζ(s)＝－Σ_n＝1～∞ Λ(n)/n^s

となることを示します。

　ζ'(s)/ζ(s)＝(logζ(s))’＝－(Σ_p∊P log [1－1/p^s])’

です。ここで、テーラ－展開

　log(1－x)＝－Σ_n＝1～∞(xⁿ/n)

を用いると、

　log [1－1/p^s]＝－Σ_n＝1～∞(p^－ns／n)

なので、ｓで微分すると

　ζ'(s)/ζ(s)＝(logζ(s))’＝Σ_p∊PΣ_n＝1～∞ (p^－ns／n)’

となります。ここで

　(p^－ns／n)’＝ (e^{－nslog p}／n)’＝－nlog p・p^－ns／n＝－log p・p^－ns

に注意すると、

　－ζ'(s)/ζ(s)＝Σ_p∊PΣ_n＝1～∞log p・p^－ns

　　　　　＝Σ_p∊P (log p／p^s＋log p／p^2s＋log p／p^3s＋log p／p^4s＋・・・)

　　　　　＝log 2／2^s＋log 3／3^s＋log 5／5^s＋log 7／7^s＋・・・

            　　　＋log 2／2^2s ＋log 3／3^2s＋log 5／5^2s＋log 7／7^2s＋・・・

　　　　　　＋log 2／2^3s＋log 3／3^3s＋log 5／5^3s＋log 7／7^3s＋・・・

　　　　　　＋log 2／2^4s＋log 3／3^4s＋log 5／5^4s＋log 7／7^4s＋・・・

　　　　　＝log 2／2^s＋log 3／3^s＋log 2／4^s＋log 5／5^s＋log 7／7^s＋log 2／8^s

　　　　　　＋log 3／9^s＋log 11／11^s＋log 13／13^s ＋log 2／16^s＋・・・

　　　　　＝Σ_n＝1～∞ Λ(n)/n^s

が得られました。一般に

　D(s)＝Σ_n＝1～∞ a_n/n^s

なる級数をディリクレ級数（Series）といいます。同じ数列a_nに対する階段関数を

　S(x)＝Σ^*_n≦x a_n

とします。ここでΣ^*はステップアップ部分は中点をとることを意味します。D(s)とS(x)はペロンの公式で結び付けられています。

＜ペロンの公式＞

D(s)＝Σ_n＝1～∞ a_n/n^sがRe(s)＞1で絶対収束するとき、c＞1に対して、

　S(x)＝1/2πi・∫_{[c－i∞、c＋i∞]} D(s)x^s/s ds

が成り立つ。これを示します。

Re(s)＞0において、

　s∫_[n,∞] x^－s－1dx＝s[x^－s /(－s)] _[n,∞]＝1/n^s

が成り立ちます。するとディリクレ級数D(s)はRe(s)＞1で絶対収束しており、

　D(s)＝Σ_n＝1～∞ a_n/n^s＝sΣ_n＝1～∞∫_[n,∞] a_n x^－s－1dx

　　　＝s(∫_[1,∞] a₁ x^－s－1dx＋∫_[2,∞] a₂ x^－s－1dx＋∫_[3,∞] a₃ x^－s－1dx＋・・・)

　　　＝s(∫_[1,2] a₁ x^－s－1dx＋∫_[2,3] (a₁＋a₂) x^－s－1dx＋∫_[3,4] (a₁＋a₂＋a₃) x^－s－1dx＋・・・)

　　　＝s・∫_[0,∞] S(x)x^－s－1dx

となります。

ここで関数f(x)に対するメリン変換M_f(s)を

　　M_f(s)＝∫_[0,∞] f(x)x^s－1dx

と定義します。すると

　D(s)/s＝M_S(－s)

と表せます。逆メリン変換M^－1[・]

　M^－1[M_f(s)] (x)＝1/2πi・∫_{[c－i∞、c＋i∞]} M_f(s)x^－s ds＝f(x)

を用いると、f(x)をS(x)に置き換えて

　S(x)＝1/2πi・∫_{[c－i∞、c＋i∞]} M_S(s)・x^－s ds

　　　＝1/2πi・∫_{[c－i∞、c＋i∞]} M_S(－s)・x^s ds

　　　＝1/2πi・∫_{[c－i∞、c＋i∞]} D(s)/s・x^s ds

が得られました。結局

　－ζ'(s)/ζ(s)＝Σ_n＝1～∞ Λ(n)/n^s＝D(s)

a_n＝Λ(n)のときのディリクレ級数D(s)になります。

Λ(n)に対する階段関数はΨ^*(x)でした。

　S(x)＝Σ^*_n≦x a_n＝Σ^*_n≦xΛ(n)＝Ψ^*(x)

よって、ペロンの公式より、c＞1に対して

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} ζ'(s)/ζ(s)・x^s/s ds

が成り立ちます。　次回はこの複素積分を実行し、マンゴルトの明示公式を導出します。

複素平面全体で正則な関数を整関数といいます。R＞0に対して、整関数f(x)の最大値を

　M(R)＝max _{[｜z｜≦R]}｜f(z)｜

位数pを

　p＝lim sup _[R→∞] loglog M(R) / logR

とします。すなわちｐは

　max _{[｜z｜≦R]}｜f(z)｜≦exp(R^p＋ε)

が成り立つｐの内で最小のものです。

＜アダマ－ルの積定理＞

整関数f(x)の位数pが有限とする。Z＝0をm₀位の零点とする。他の零点をa1、a2、a3、・・・とし、その位数をm1、m2、m 3、・・・とする。このときｐ次以下の多項式g(z)が存在して、

　f(z)＝z^m0 e^g(z) Π_n=[1～∞] E(z/a_n,p)^m_n

と表せる。ここで

　E(z,0)＝1－z、

　E(z,1)＝(1－z) exp(z)

E(z,p)＝(1－z) exp(z＋z²/2＋z³/3＋・・・＋z^p/p)　ｐ＞1

である。

例えば、整関数f(z)＝sin(πz)の場合、位数p＝1、すなわち

　max _{[｜z｜≦R]}｜sin(πz)｜≦exp(R^1＋ε)

　e^iπz＝e^iπ(－iR)＝e^πRより、

　｜sin(πz)｜＝1/2・｜e^iπz＋e^－iπz｜＜1/2・｜e^πR＋e^－πR｜＜e^π・e^R

です。sin(πz)＝0　なるzは整数全体で、z→nで

　sin(πz)/ (z－n)＝(－1)ⁿ・sin(π(z－n)) / (z－n)　→　(－1)ⁿ

なので、全て1位の零点を有します。n∊Zに対して

　a_n＝n、m₀＝1、m_n＝1、g(z)＝az＋b

です。n≠0で

　sin(πz)＝z¹・exp(az＋b)・Π’_{n=[－∞～∞]} E(z/n,1)¹ 　　(n≠0)

　E(z,1)＝(1－z) exp(z)

だから、

sin(πz)＝z・exp(az＋b)・Π’_{n=[－∞～∞]} (1－z/n) exp(z/n)

　　　＝z・exp(az＋b)・Π_n=[1～∞] (1＋z/n) exp(－z/n) (1－z/n) exp(z/n)

　　　＝z・exp(az＋b)・Π_n=[1～∞] (1－z²/n²)

対数微分をとれば

　π・cos(πz)/ sin(πz)＝1/z＋a＋Σ_n=[1～∞]2z/ (z²－n²)

となります。すべて奇関数なので、a＝0となります。C＝e^bと置くと

　sin(πz)＝Cz・Π_n=[1～∞] (1－z²/n²)

　C＝lim_[z→0] π・sin(πz)／πz／Π_n=[1～∞] (1－z²/n²)＝π

よって

　sin(πz)＝πz・Π_n=[1～∞] (1－z²/n²)

が得られます。確かにz＝0、±nのときに零点になっています。

上式を展開すると

　sin(πz)＝πz－1/6・(πz)³＋1/5！・(πz)⁵＋・・・

　　　　＝πz・(1－Σ_n=[1～∞] z²/n²＋Σ_n>m≧1 z⁴/n² m²＋・・・)

z³の係数を較べて、

　－π³/6＝－πΣ_n=[1～∞] /n²＝－πζ(2)

　　ζ(2) ＝π²/6

が得られます。同様にz⁵の係数を較べて、

　π⁵/120＝πΣ_n>m≧1 z⁴/n² m²

　ζ(2) ²＝[Σ_n=[1～∞] 1 /n²]・[Σ_m=[1～∞]1 /m²]

　　　＝Σ_m=[1～∞] 1 /n⁴＋2Σ_n>m≧1 z⁴/n² m²

　(π²/6) ²＝ζ(4)＋2・π⁴/120

　ζ(4)＝π⁴/36－π⁴/60＝π⁴ (5/180－3/180)＝π⁴/90

が得られます。

＜ガンマ関数の積表示＞

ガンマ関数1/Γ(z)は整関数で、0以下の整数が位数1の零点でした。アダマ－ルの積定理より、

　1/Γ(z)＝ze^az＋bΠ_n=[1～∞] (1＋z/n) exp(－z/n)

よって

　1/zΓ(z)＝1/Γ(z＋1)＝e^az＋bΠ_n=[1～∞] (1＋z/n) exp(－z/n)

ここでz＝0とおくと

　1＝1/Γ(0＋1)＝e^a0＋bΠ_n=[1～∞] (1＋0/n) exp(－0/n)＝e^b

よって

　1/Γ(z)＝ze^azΠ_n=[1～∞] (1＋z/n) exp(－z/n)

ここでz＝1とおくと

　1/Γ(1)＝1e^aΠ_n=[1～∞] (1＋1/n) exp(－1/n)

対数をとって

　0＝ａ＋Σ_n=[1～∞][ log(1＋1/n)－1/n]

aの値は

　a＝lim_N→∞Σ_n=[1～N][ 1/n－log(n＋1)－logn)]

　　＝lim_N→∞　Σ_n=[1～N](1/n)－log(N＋1)

　　＝lim_N→∞　Σ_n=[1～N](1/n)－logN＋log(N/ (N＋1))

　　＝lim_N→∞　Σ_n=[1～N](1/n)－logN

　　＝γ

となります。γはオイラ－の定数と呼ばれる値で、γ＝0.57721・・・です。従って

　1/Γ(z)＝ze^γzΠ_n=[1～∞] (1＋z/n) exp(－z/n)

　1/Γ(－z)＝－ze^－γzΠ_n=[1～∞] (1－z/n) exp(＋z/n)

です。Γ(1－z)＝－zΓ(－z)より

　1/Γ(z)Γ(1－z)

＝－1／zΓ(z)Γ(－z)

＝1/z・ze^γzΠ_n=[1～∞] (1＋z/n) exp(－z/n)・ze^－γzΠ_n=[1～∞] (1－z/n) exp(＋z/n)

＝zΠ_n=[1～∞] (1＋z/n) (1－z/n)

＝zΠ_n=[1～∞] (1－z²/n²)

＝sin(πz)/π

となり、相反定理が得られます。

 

＜ゼ－タ関数の関数等式とテータ関数の関係＞

ゼ－タ関数の関数等式は

　ξ(x)＝π^－s/2Γ(s/2)ζ(s)

とおくと

　ξ(x)＝ξ(1－x)

で表されます。テータ関数

　θ(t)＝Σ_{n＝[－∞、∞]} e^{－πtn^2}

の変換公式は

　θ(t)＝θ(1/t)/√t

でした。

　Ψ(t)＝Σ_{n＝[1、∞]} e^{－πtn^2}

とおくと、

　θ(t)＝1＋2Ψ(t)

が成り立ちます。Γ関数の定義において、

　Γ(s)＝∫_[0、∞] x^s－1e^－xdx　(s＞0)

x＝πtn²と変数変換すると、dx＝πn²dtとなり

　Γ(s)＝∫_[0、∞] (πtn²)^s－1e^{－πtn^2}πn² dt

　　　＝π^sn^2s∫_[0、∞] t^s－1e^{－πtn^2} dt

なので

　Γ(s/2)＝π^s/2n^s∫_[0、∞] t^s/2－1e^{－πtn^2}dt

両辺をπ^s/2n^sで割って

　π^－s/2・1/n^s Γ(s/2)＝∫_[0、∞] t^s/2－1e^{－πtn^2} dt

これを全ての自然数nについて加えれば

　π^－s/2・Γ(s/2) [Σ_{n＝[1、∞]} 1/n^s]＝∫_[0、∞] t^s/2－1[Σ_{n＝[1、∞]} e^{－πtn^2}]dt

　π^－s/2・Γ(s/2)ζ(s) ＝∫_[0、∞] t^s/2－1Ψ(t) dt

を得ます。　

　右辺＝∫_[0、1] t^s/2－1Ψ(t) dt＋∫_[1、∞] t^s/2－1Ψ(t) dt

として、第一項で、t＝1/uと変数変換すると、dt＝－1/u² duより

　∫_[0、1] t^s/2－1Ψ(t) dt＝－∫_[∞、1] (1/u)^s/2－1Ψ(1/u) 1/u² du

 　　　　　　　　　　＝∫_[1、∞] u^－s/2－1Ψ(1/u) du

ここで

　　1＋2Ψ(u)＝θ(u)＝θ(1/u)/u^1/2＝[1＋2Ψ(1/u)]/u^1/2

となることから、

　Ψ(1/u)＝u^1/2Ψ(u)＋1/2・u^1/2－1/2

を得ます。これを代入すると

　∫_[0、1] t^s/2－1Ψ(t) dt

　＝∫_[1、∞] u^－s/2－1[u^1/2Ψ(u)＋1/2・u^1/2－1/2]du

　＝∫_[1、∞] u^{(1－s)/2－1}Ψ(u) du ＋1/2∫_[1、∞] u^{(1－s)/2－1} du－1/2∫_[1、∞] u^－s/2－1du

　＝∫_[1、∞] u^{(1－s)/2－1}Ψ(u) du ＋1/(s－1)－1/s

　＝∫_[1、∞] u^{(1－s)/2－1}Ψ(u) du －1／s(1－s)

となります。なぜなら、s>0より

　1/2∫_[1、∞] u^{(1－s)/2－1}du＝1/2・2/(1－s) [u^(1－s)/2]_u＝1、∞＝1/(s－1)　

　－1/2∫_[1、∞] u^－s/2－1du＝－1/2・(－2/s)[u^－s/2]_u＝1、∞＝－1/s

よって

　右辺＝∫_[0、1] t^s/2－1Ψ(t) dt＋∫_[1、∞] t^s/2－1Ψ(t) dt

　　　＝∫_[1、∞] u^{(1－s)/2－1}Ψ(u) du －1／s(1－s)＋∫_[1、∞] t^s/2－1Ψ(t) dt

　　　＝∫_[1、∞] [u^{(1－s)/2－1}＋u^s/2－1]Ψ(u) du －1／s(1－s)

となります。右辺は全ての実数sに対して積分が存在し、sを1－sに置き換えても、式が変わりません。

　左辺：ξ(s)＝π^－s/2・Γ(s/2)ζ(s)

とすると、

　ξ(s)＋1／s(1－s)＝∫_[1、∞] [t^{(1－s)/2－1}＋t^s/2－1]Ψ(t) dt

は全ての実数sで定義され、関数等式

　ξ(s)＝ξ(1－s)

が成り立ちます。

 

＜ζ’(0)の計算＞

ここでは

　ζ’(0)＝－1/2・log(2π)

を示します。

複素数sに対して、イ－タ関数

　η(s)＝1－1/2^s＋1/3^s－1/4^s＋・・・

はRe(s)＞0で収束し、この範囲で正則です。

イ－タ関数は

　｜η(s)｜＝｜1－1/2^s＋1/3^s－1/4^s＋・・｜≦1＋1/2^s＋1/3^s＋1/4^s＋・・＝ζ(s)

よりRe(s)＞1で収束することは明らかです。

イ－タ関数とゼ－タ関数には

　η(s)＝(1－2^1－s)ζ(s)

なる関係がありました。

　Lim_[s→1] η(s)＝Lim_[s→1] (1－2^1－s)/(s－1)・(s－1)ζ(s)

　　　　　＝Lim_[t→0] (2⁰－2^－t)/t・Lim_[s→1] (s－1)ζ(s)

　　　　　＝－Lim_[t→0] (2⁰－2^－t)/(0－t)・1

　　　　　＝Lim_[t→0] (－2^－t)’

　　　　　＝log2

ここで

　(－2^－t)’＝ (－e^－tlog2)’ ＝ log2 (e^－tlog2)＝log2・2^－t

を用いました。つまりs＝1はη(s)の除去可能な特異点であり、η(s)はs＝1で正則です。

ここでイ－タ関数の部分和

　η_N(s)＝Σ_n＝1～N　(－1)^n－1/n^s

を考えると　

　η_2＜η_4＜η_{6＜・・＜}η_2N＜η_2N＋2＜η_2N＋1＜η_{2N－1＜・・＜}η_5＜η_3＜η₁

なので、Re(s)＞0ならば

　Lim_[N→∞] (η_2N－η_2N－1)＝－Lim_[N→∞]1/(2N)^S＝0

だから

　Lim_[N→∞] η_2N＝Lim_[N→∞]η_2N－1＝η(s)

となります。イ－タ関数η(s)はRe(s)＞0で収束し、この範囲で正則です。

先ほどの関係式

　η(s)＝(1－2^1－s)ζ(s)

の両辺を微分すると

　η’(s)＝log2・2^1－sζ(s)＋(1－2^1－s)ζ’(s)

となります。s＝0を代入すると

η’(0)＝log2・2^1－0ζ(0)＋(1－2^1－0)

　　　＝log2・2・(－1/2)－ζ’(0)

　　　＝－log2－ζ’(0)

が得られます。η’(0)を求めるために、η(s)を変形すると

η(s)＝1－1/2^s＋1/3^s－1/4^s＋・・・

　　＝1/2[1+1－1/2^s－1/2^s＋1/3^s＋1/3^s－1/4^s－1/4^s＋・・・]

　　＝1/2+1/2 [(1－1/2^s)－(1/2^s－1/3^s)＋(1/3^s－1/4^s)－(1/4^s－1/5^s)＋・・・]

η(s)は全複素平面で正則なため、両辺を微分すると

　η’(s)＝1/2 [(0＋log2/2^s)－(－log2/2^s＋log 3/3^s)＋(－log 3/3^s＋log4/4^s)－(－log4/4^s＋log5/5^s)＋・・・]

となります。この右辺はRe(s)＞0の範囲で広義一様収束していることから、ｓ→＋0の極限をとると、

　η’(0)＝1/2 [log2－(－log2＋log 3)＋(－log 3＋log4)－(－log4＋log5)＋・・・]

　　　＝1/2・log(2/1・2/3・4/3・4/5・・・)

　　　＝1/2・log(π/2)

となります。ここでウォリスの公式を用いました。従って

　　　ζ’(0)＝－η’(0) －log2

　　　　　　＝－1/2・log(π/2) －1/2・log4

　　　　　　＝－1/2・log(2π)

が得られます。

 　η(0)＝(1－2^1－0)ζ(0)＝－1(－1/2)＝1/2

ですから、まとめると

　ζ(0)＝－1/2、ζ’(0)＝－1/2・log(2π)

　η(0)＝＋1/2、η’(0)＝＋1/2・log(π/2)

が成り立ちます。

＜ガンマ関数の解析接続＞

Γ関数は

　Γ(s)＝∫_[0、∞] t^s－1e^－tdt

で定義されています。sを複素数に拡張した場合に、区間[0、∞]での積分は収束するか調べて見ましょう。

s＝x＋iyとして、0＜x₀＜x₁なる任意の実数を用いて、0＜x₀＜x＜x₁とすれば、

　  Γ(s)＝∫_[0、1] t^s－1e^－tdt＋∫_[1、∞] t^s－1e^－tdt

　｜Γ(s)｜≦ ∫_[0、1] ｜t^s－1｜e^－tdt ＋ ∫_[1、∞] ｜t^s－1｜e^－tdt

であり、

　(1/2)^x＜(1/2)^x0　、2^x＜(2)^x1

に注意すると、

∫_[0、1] ｜t^s－1｜e^－tdt＝∫_[0、1] t ^x－1e^－tdt≦∫_[0、1] t ^x0－1e^－tdt≦∫_[0、∞] t ^x0－1e^－tdt＝Γ(x₀)

∫_[1、∞] ｜t^s－1｜e^－tdt＝∫_[1、∞] t ^x－1e^－tdt≦∫_[1、∞] t ^x1－1e^－tdt≦∫_[0、∞] t ^x1－1e^－tdt＝Γ(x₁)

ですから、

｜Γ(s)｜≦Γ(x₀)＋Γ(x₁)

が成り立ちます。従って0＜x₀＜Re(s)＜x₁において、ε→0のとき

　Γ_ε(s)＝∫_[ε、1/ε] t^s－1e^－tdt　→　Γ(s)＝∫_[0、∞] t^s－1e^－tdt　

となり、Γ_ε(s)はΓ(s)に一様収束します。Γ_ε(s)は有限区間での積分だから、sの正則関数です。

一様収束極限であるΓ(s)もx₀＜Re(s)＜x₁における正則関数です。x₀、x₁は任意だから、

Γ(s)はRe(s)＞0におけるsの正則関数になっています。nを任意の自然数とすれば、

　Γ(s)＝Γ(s＋n)／s(s＋1) (s＋2)・・ (s＋n－2) (s＋n－1)

が成り立ちます。Γ(s)はRe(s)＋n＞0における有理型関数で、s＝0,－1,－2,・・・－n+1でを1位の極とする以外は、正則になっています。nは任意なので、Γ(s)は複素数全体で正則な有理型関数で、s＝0,－1,－2,・・・で1位の極をもっています。Γ(1－s)は、s＝0,1,2,・・・で1位の極をもっています。さらに整数でない実数sに対して

　Γ(s)Γ(1－s)＝π/sin(πs)

が成り立ちます。複素関数論の一致の定理より、整数でない複素数に関して、この等式は成り立っています。この等式から、ガンマ関するΓ(s)は零点を持たない有理型関数であることが分かります。よって1/Γ(s)は複素数全体で正則な関数になっています。

＜リ－マン関数等式からオイラ－関数等式の導出＞

関数等式には、非対称型のオイラ－による関数等式

　ζ(1－s)=cos(sπ/2) Γ(s)ζ(s)／2^s－1π^s・・・・（1）

と対称型のリ－マンによる関数等式

　π^－s/2Γ(s/2)ζ(s)＝π^－(1－s)/2Γ((1－s)/2)ζ(1－s) ・・・・（2）

がありました。これまでオイラ－による関数等式からリ－マンによる関数等式を導出しました。今度は逆にリ－マンによる関数等式からオイラ－による関数等式を導出します。

(2)の両辺に(－s)Γ(－s/2)を掛けると、

　π^－s/2(－s)Γ(－s/2)Γ(s/2)ζ(s)＝π^－(1－s)/2(－s)Γ(－s/2)Γ((1－s)/2)ζ(1－s)

左辺の係数は

　π^－s/2 2(－s/2)Γ(－s/2)Γ(s/2)＝2π^－s/2Γ(1－s/2)Γ(s/2)＝π^－s/2 2π/ sin(πs/2)

となります。ここで、ガンマ関数の相反公式：Γ(s/2)Γ(1－s/2)＝π/sin(πs/2)を用いました。ルジャンドルの2倍公式

　Γ(2s)＝2^2s－1/π^1/2・Γ(s) Γ(s+1/2)

でs→－s/2に置き換えた

　Γ(－s)2^s+1π^1/2＝Γ(－s/2) Γ((1－s)/2)

を用いると、右辺の係数は

　π^－(1－s)/2 (－s)Γ(－s/2)Γ((1－s)/2)＝π^－(1－s)/2 (－s)Γ(－s) 2^s+1π^1/2

　　＝2^s+1π^s/2Γ(1－s)

となります。従って、左辺＝右辺は

　π^－s/22π/ sin(πs/2)ζ(s)＝2^s+1π^s/2Γ(1－s)ζ(1－s)

となります。

　ζ(s)＝2^sπ^s－1Γ(1－s)ζ(1－s) sin(πs/2) ・・・・（*）

が得られます。s→1－sに置き換えると

　sin(π(1－s) /2)＝sin(π/2)cos(－πs/2)＝cos(πs/2)

より

　ζ(1－s)＝Γ(s)ζ(s) cos(πs/2)／2^s－1π^s・・・・（1）

が得られます。

＜ゼ－タ関数の自明な零点はs＝－2k＞

　ζ(s)＝2^sπ^s－1Γ(1－s)ζ(1－s) sin(πs/2) ・・・・（*）

ζ(1－s)は1－s＞1、すなわち、s＜0で定義されています。

　sin(πs/2)＝0　→　s＝－2、－4、－6、・・－2k、・・・

なる負の偶数では

　ζ(－2k)＝0　for　k＝1、2、3・・・

が成り立ちます。これをζ(s) の自明な零点と言います。

また、この公式からζ(0)の値が得られます。

lim_[s→1] (s－1)ζ(s)＝1　→　lim_[s→0] ((1－s)－1)ζ(1－s)＝1

に注意すると

ζ(0)＝lim_[s→0] 2^sπ^s－1Γ(1－s)ζ(1－s) sin(πs/2)

　　　＝－1/2・Γ(1) lim_[s→0]sin(πs/2)/(πs/2)・(1－s－1)ζ(1－s)

　　　＝－1/2

となります。

 

＜ルジャンドルの2倍公式の証明＞

　Γ(2s)＝2^2s-1/π^1/2・Γ(s) Γ(s+1/2)

を証明する。

今、B(x,y)＝Γ(x)Γ(y)/Γ(x＋y) より

　B(x,1/2)＝Γ(x)Γ(1/2)/Γ(x+1/2)

　B(x,x)＝Γ(x)² /Γ(2x)

が成り立つ。先ほど証明された式

　B(x,1/2)＝2^2x－1B(x,x)

に代入すると、

　Γ(x)Γ(1/2)/Γ(x+1/2)＝2^2x－1Γ(x)² /Γ(2x)

を得る。Γ(1/2)＝π^1/2より

　Γ(2x)＝2^2x－1π^－1/2Γ(x)Γ(x+1/2)

が成り立つことが示された。

Γ(n)=(n-1)!　、Γ(1/2)=π^－1/2なので、ｘ＝4のとき

Γ(8)＝2^2*4－1π^－1/2Γ(4)Γ(4+1/2)＝2³Γ(4)・2⁴Γ(4+1/2)π^－1/2

2⁴Γ(4+1/2)π^－1/2＝2⁴・7/2 Γ(7/2)π^－1/2＝2⁴・7/2・5/2・3/2・1/2 Γ(1/2)π^－1/2

　　　　　　　＝7・5・3・1

2³Γ(4)＝2³（3・2・1）＝6・4・2

Γ(8)＝7！＝7・5・3・1・6・4・2

を表しています。

＜ガンマ関数の相反公式＞

　Γ(x)Γ(1－x)＝π/sin(πx)

を証明します。その前にこの公式の直感的な説明をします。

Γ(x)はｘ＝0，-1，-2，・・・でのみ1位の極をもちます。Γ(1-x)はｘ＝1，2，3，・・・でのみ1位の極をもちます。

f(x)=1/Γ(x)Γ(1－x)は全ての整数で1位の零点をもちます。ｘをｘ+1にすると

　Γ(ｘ+1)Γ(1-（ｘ+1））＝ｘΓ(ｘ)Γ(-ｘ）＝-ｘΓ(ｘ)Γ(1-ｘ）

ので、f(x+2)＝－f(x+1)＝f(x)　となり、f(x)は周期2の関数であることが分かります。ｘ＝1/2で最大値

　f(1/2)＝1/Γ(1/2)Γ(1－1/2)＝1/π

をとります。よってf(x)＝sin(πx)/πと予想できます。

証明に入ります。先ほどもとめたベータ関数の性質は

（4）：B(x,1－x)＝∫_[0，∞] u^x－1/(1＋u) du

（5）：B(x,1－x)＝Γ(x)Γ(1－x)

ですから、

　∫_[0，∞] x^a－1/(1＋x) dx＝π/sin(πa)　0＜a＜1

を示せばよいことが分かります。

D積分閉路を使って

　f(z)＝z^a－1/(1＋z)

の複素積分を行います。D積分閉路は

　D＝C₁＋C₂(ε)＋C₃＋C_R

からなります。

 

 

 

 

 

ε→0、R→∞で

　∫_C2(ε)f(z)dz→0、∫_CR f(z)dz→0

となります。0＜a＜1より、－1＜a－1＜0、に注意すると

　－ε+1≦εe^iθ+1≦ε+1より、1/｜(εe^iθ＋1)｜≦1/(1－ε)

なので、z＝εe^iθ、dz＝iεe^iθdθ、0＜a＜1、より

　｜∫_C2(ε)f(z)dz｜≦∫_[0、2π]｜(εe^iθ) ^a－1｜/｜εe^iθ＋1｜｜iεe^iθ｜dθ

　　　　　　　≦εε^a－1/(1－ε) 2π＝2πε^a/(1－ε)　→　0　as　ε→0

同様に、－1＜a－1＜0、より

　｜∫_CRf(z)dz｜≦∫_[0、2π]｜(Re^iθ) ^a－1｜/｜Re^iθ＋1｜｜iRe^iθ｜dθ

　　　　　　　≦2πR・R^a－1/R＝2πR^a－1→　0　as　R→∞

となります。

z ^a－1はz＝0で特異点を持ちますが、z＝0は経路D内には含まれません。

D積分閉路内の極は、z＝－1だけです。f(z)のz＝－1での留数は

　Res[f,－1]＝lim_[x→－1] (z＋1) z ^a－1/(z＋1)＝(e^iπ) ^a－1＝e^iπa e^－iπ＝－e^iπa

　∫_D f(z)dz＝2πi Res[f,－1]＝2πi (－e^iπa)

となります。

C₃上での偏角は0だからz＝xe⁰代入して、ε→0、R→∞で

　∫_C3 f(z)dz＝∫_[ε、R] x^a－1/(1＋x) dx　→　I＝∫_[0、∞] x^a－1/(1＋x) dx

C₁上での偏角は2πなので、z＝xe^2πi代入して、ε→0、R→∞で

　z^a－1＝(xe^2πi) ^a－1＝x ^a－1e^2πiae^－2πi＝x ^a－1e^2πia

　∫_C1 f(z)dz＝∫_[R、ε] e^2πia x^a－1/(1＋x) dx　→∫_[0、∞] x^a－1/(1＋x) dx

となります。従って

　2πi (－e^iπa)＝I＋0＋I＋0＝(1－e^2πia)I

これをIについて解くと

　I＝2πi (－e^iπa)/ (1－e^2πia)＝2πi (－e^iπa)／(－e^iπa) (e^iπa－e^－iπa)

　　＝π/sin(πa)

が得られます。

 

ゼ－タ関数とガンマ関数とベータ関数は相互に密接な関係があります。ここではベータ関数のいくつかの性質を紹介します。これらはルジャンドルの倍公式やガンマ関数の相反公式を証明するのに役立ちます。

＜ベ－タ関数の諸性質＞

ベ－タ関数は

　B(x,y)＝∫_[0，1] t^x－1(1－t)^y－1dt  (x>0,y>0)

で定義されます。

（1）B(x,y)＝B(y,x)

　t’＝1－tとおくと、

B(x,y)＝－∫_[1，0] (1－t’)^x－1 t’^y－1dt’ ＝B(y,x)

（2）B(x,y)＝2∫_[0，π/2] sin^2x－1θcos^2y－1θdθ

　　t＝sin²θとおくと、dt＝2sinθcosθdθ

　　B(x,y)＝∫_[0，π/2] (sin²θ)^x－1(cos²θ)^y－12sinθcosθdθ

　　　　＝2∫_[0，π/2] sin^2x－1θcos^2y－1θdθ

（3）B(x,y)＝Γ(x)Γ(y) /Γ(x＋y)

　　t＝s²とおくと、dt＝2sdsより

　　Γ(x)＝∫_[0，∞] t^x－1 e^－t dt＝2∫_[0，∞] s^2x－1 e^－ss ds

　　Γ(x)Γ(y)＝4∫_[0，∞] t^2x－1 e^－tt dt・∫_[0，∞] s^2y－1 e^－ss ds

　　t＝rcosθ、s＝rsinθとおくと、t²＋s²＝r²、dtds＝rdrdθ

　　4∫_[0，π/2]dθ∫_[0，∞] dr (rcosθ)^2x－1 (rsinθ)^2y－1 e^－rr

　＝2∫_[0，π/2]dθ∫_[0，∞] dr cos^2x－1θsin^2y－1θ・2∫_[0，∞] r^2(x＋y)－2e^－rr rdr

　t＝r²とおくと、dt＝2rdrより、r^2(x＋y)－2＝t^(x＋y)/r²＝t^(x＋y)－1

　　Γ(x)Γ(y)＝B(x,y)・∫_[0，∞] t^(x＋y)－1e^－t dt＝B(x,y)・Γ(x＋y)

が示された。

（4）B(x,y)＝∫_[0，∞] u^x－1/(1＋u)^x＋y du

　　B(x,y)＝∫_[0，1] t^x－1(1－t)^y－1dt 

　において、t＝u/(1＋u)とおくと　

　　1－t＝1－u/(1＋u)＝1/(1＋u)

　(1＋u)t＝u、u－ut＝t、u＝t/(1－t)　→u＝0～∞
　du＝[(1－t)+t]/(1－t)² dt＝1/(1－t)² dt＝(1＋u) ² dt

　→　dt＝du/(1＋u) ²

であるから

　t^x－1(1－t)^y－1dt＝[u/(1＋u)]^x－1(1＋u)^－y＋1(1＋u)^－2du
＝u^x－1(1＋u)^－(x＋y) du

　B(x,y)＝∫_[0，∞] u^x－1(1＋u)^－(x＋y) du

が示された。

y＝1－xのとき

　B(x,1－x)＝∫_[0，∞] u^x－1(1＋u)^－(x＋y) du

　　　　　＝∫_[0，∞] u^x－1/(1＋u) du

が成り立つ。

（5）B(x,1－x)＝Γ(x)Γ(1－x)

　B(x,y)＝Γ(x)Γ(y)/Γ(x＋y) において

　　y＝1－xと置くと、Γ(x＋y)＝Γ(1)＝1より

　B(x,1－x)＝Γ(x)Γ(1－x)/Γ(1)＝Γ(x)Γ(1－x)

（6）B(x,1/2)＝2^2x－1B(x,x)

　B(x,1/2)＝B(1/2 ,x)＝∫_[0，1] t^－1/2 (1－t) ^x－1dt

　t＝u²とおくと、t^－1/2＝u^－1、dt＝2udu

　B(x,1/2)＝2∫_[0，1] (1－u²)^x－1 du

　　　　＝∫_[0，1] (1－u²)^x－1 du－∫_[0，－1] (1－u²)^x－1 d(－u)

　　　　＝∫_[0，1] (1－u²)^x－1 du＋∫_[－1，0] (1－u²)^x－1 du

　　　　＝∫_[－1，1] (1－u²)^x－1 du

　s＝(1+u)/2とおくと、u＝2s－1、s＝0～1

　　1－u＝1－2s+1＝2(1－s)

　　1－u²＝(1－u) (1＋u)＝4(1－s)s

　B(x,1/2)＝2∫_[0，1] (4(1－s)s)^x－1 2ds

　　　　＝2^2x－1∫_[0，1] (1－s) ^x－1s^x－1 ds

　　　　＝2^2x－1B(x,x)

が示された。

 

＜ゼ－タ関数の関数等式の証明＞

関数等式には、非対称型のオイラ－による関数等式

　ζ(1－s)=cos(sπ/2) Γ(s)ζ(s)／2^s－1π^s・・・・（1）

と対称型のリ－マンによる関数等式

　π^－s/2Γ(s/2)ζ(s)＝π^－(1－s)/2Γ((1－s)/2)ζ(1－s) ・・・・（2）

があります。関数等式はゼ－タ関数の定義域を拡大する場面でよく用いられす。

ここではオイラ－による関数等式を導出し、その後

ガンマ関数の相反公式

   Γ(s)Γ(1－s)＝π/sin(πs)

においてs→(1－s)/2に置き換えた

　Γ((1－s)/2)Γ((1＋s)/2)＝π/cos(πs/2)　　・・・（5）

の式とルジャンドルの2倍公式

　Γ(2s)＝2^2s-1/π^1/2・Γ(s) Γ(s+1/2)

においてs→s/2に置き換えた

　Γ(s)＝2^s-1/π^1/2・Γ(s/2) Γ((s+1)/2) 　・・・（6）

式を用いて、リ－マンによる関数等式を導出します。

その前に、ゼ－タ関数の積分表示を求めましょう。

＜ゼ－タ関数の積分表示＞

ゼ－タ関数：ζ(s)＝Σ_n＝1-∞ 1/n^s

ガンマ関数：Γ(s)＝∫_[0、∞] x^s－1e^－xdx

のとき、s＞1に対して

　∫_[0、∞] x^s－1/(e^x－1)dx=ζ(s) Γ(s)

が成り立つ。

[証明]

　1/(e^x－1)＝e^－x/(1－e^－x)＝Σ_n=1-∞ (e^－x)ⁿ ＝Σ_n=1-∞ e^{－n x}

を代入すると、

∫_[0、∞] x^s－1/(e^x＋1)dx=∫_[0、∞] x^s－1Σ_n=1-∞ e^{－n x} dx

                   =Σ_n=1-∞∫_[0、∞] x^s－1 e^{－n x} dx

ここで、y＝nx　と変数変換すると

　∫_[0、∞] x^s－1/(e^x＋1)dx =Σ_n=1-∞∫_[0、∞] (y/n)^s－1 e^－y dy/n

=Σ_n=1-∞1/n^s∫_[0、∞] y^s－1 e^－y dy

＝ζ(s)Γ(s)

が示されました。

＜オイラ－による関数等式の導出＞

複素積分
　I(s)＝∫_C z^s－1/(e^z－1)dz

を2つの積分経路で求めて、等値することで(1)式のオイラ－による関数等式を導出します。

1）ハンケル積分経路による積分計算

Cをハンケル積分経路とすると、全複素平面で

　∫_C z^s－1/(e^z－1)dz＝(e^2πsi－1) ζ(s)Γ(s)　　　・・・・（3）

が成立することを示します。

Ｃは以下の3つの経路

　C1：z＝x＋iε　x＝∞→r

　C2：z＝re^iθ　θ＝0→2π

　C3：z＝x－iε　x＝r→∞

から成ります。

　I(s)＝∫_C z^s－1/(e^z－1)dz

　　＝∫_C1 z^s－1/(e^z－1)dz＋∫_C2 z^s－1/(e^z－1)dz＋∫_C3 z^s－1/(e^z－1)dz

である。まず経路1での積分はε→0で

　I₁(s)＝∫_C1 z^s－1/(e^z－1)dz＝－∫_[0、∞] x^s－1/(e^x－1)dx

となる。経路2の積分はr→0で

｜I₂(s)｜＝｜∫_C2 z^s－1/(e^z－1)dz｜≦∫_[0，2π] r^s/[(e^r－1)/r]dθ≦r^s・2π→　0　as r→0  s＞0

ゼロになる。経路3では、原点の周りの1回転して位相2πが付加されるので

　z ^s－1＝(re^i2π) ^s－1＝r ^s－1e^i2πs

より、e^i2πsが残る。rをxに置き換えて0から∞まで積分すると、

　I₃(s)＝∫_C3 z^s－1/(e^z－1)dz＝e^i2πs∫_[0、∞] x^s－1/(e^x－1)dx

従って、ε→0、r→0の極限では、ゼ－タ関数の積分表示を用いて

　I(s)＝－∫_[0、∞] x^s－1/(e^x－1)dx＋　0　＋e^i2πs∫_[0、∞] x^s－1/(e^x－1)dx

　　　＝(e^i2πs－1) ∫_[0、∞] x^s－1/(e^x－1)dx

　　　＝(e^i2πs－1) ζ(s)Γ(s)

が示されました。

ここでs＝1のとき

　e^i2πs－1＝0

なので、s＝1は(e^i2πs－1)の1位の零点です。ζ(s)＝1/(s－1)+F(s)と書け、ζ(s)はs＝1で1位の極を持ちます。従って、(e^i2πs－1)ζ(s)はs＝1で正則になっています。上式は全ての複素数sで成り立っています。

 

2）D積分経路による積分計算

下図のように積分経路Dを取ります。全複素平面で

∫_C z^s－1/(e^z－1)dz＝－∫_D z^s－1/(e^z－1)dz＝(2π)^s(e^3πsi/2－e^πsi/2)ζ(1－s)　・・（4）

が成立することを示します。

経路Dは

　D＝C₁＋C₂＋C₃＋C_R

から成ります。経路Dの4つの経路は

　C₁：z＝x－iε　x＝∞→r

　C₂：z＝re^iθ　θ＝2π→0

　C₃：z＝x＋iε　x＝∞→r

　C_R：z＝Re^iθ　θ＝0→2π

です。分母にe^zがあるのでC_Rに関する積分はR→∞でゼロになります。ところで

C₁＋C₂＋C₃の経路での積分は先ほどのハンケル積分経路と逆向きなので、

　∫_C z^s－1/(e^z－1)dz＝－∫_D z^s－1/(e^z－1)dz

となります。被積分関数の分母はz＝±2nπiでゼロになります。経路Dは、被積分関数の極、z＝±2πi、±4πi、±6πi、・・±2nπi（＜Ri）を含んでいます。従って経路Cでの積分は、経路D内の積分の留数の和を求めて、全体にマイナス符号をつければ得られます。

　z＝2nπiでの留数は、ｎ＞0のとき偏角はπ/2なので（i＝e^iπ/2)

　I_＋＝lim _[z→2nπi] (z－2nπi)・ z^s－1/(e^z－1)
　　＝lim _[z→2nπi]・ z^s－1／(e^z－e^2nπi )/
　　＝lim _[z→2nπi]・ z／(e^z)’

　　＝(2nπi) ^s－1

　　＝(2nπ) ^s－1(e^iπ/2) ^s－1

　　＝－i・(2nπ) ^s－1・e^iπs/2

となります。

　z＝－2nπiでの留数は、偏角は3π/2なので、（－i＝e^i3π/2)

I_－＝(－2nπi) ^s－1

　＝(2nπ) ^s－1(e^i3π/2) ^s－1

　＝i・(2nπ) ^s－1・e^i3πs/2

となります。R→∞のとき、ｎ＝1～∞の全ての留数の和を求めると、

　∫_D z^s－1/(e^z－1)dz＝Σ_n 2πi・(I_＋＋I_－)

　　　　　　　　　＝Σ_n 2πi[－i・(2nπ) ^s－1・(e^iπs/2－e^i3πs/2)]
　　　　　　　　　＝(2π) ^s(e^iπs/2－e^i3πs/2)・Σ_n 1/n ^1－s

　             　　　　 ＝(2π) ^s(e^iπs/2－e^i3πs/2)・ζ(1－s)

従って、

    ∫_C z^s－1/(e^z－1)dz＝(2π) ^s(e^i3πs/2－e^iπs/2)ζ(1－s)

が示されました。

＜オイラ－による関数等式の導出＞

2つの積分経路で求めた

   I(s)＝∫_C z^s－1/(e^z－1)dz

の値を等値することで、オイラ－による関数等式（非対称型）

　ζ(1－s)=cos(sπ/2) Γ(s)ζ(s)／2^s－1π^s・・・・（1）

を導出します。

2つの積分経路で求めた値は
　∫_C z^s－1/(e^z－1)dz＝(e^2πsi－1) ζ(s)Γ(s)　　・・・（3）

   ∫_C z^s－1/(e^z－1)dz＝－∫_D z^s－1/(e^z－1)dz＝(2π)s(e^3πsi/2－e^πsi/2) ζ(1－s)　・・（4）

でした。よって

   (e^2πsi－1) ζ(s)Γ(s)＝(2π)^s(e^3πsi/2－e^πsi/2) ζ(1－s)　

が成り立ちます。

　(e^2πsi－1)/ (e^3πsi/2－e^πsi/2)＝e^πsi(e^πsi－e^－πsi) / e^πsi (e^πsi/2－e^－πsi/2)

　＝(e^πsi/2＋e^－πsi/2) (e^πsi/2－e^－πsi/2) / (e^πsi/2－e^－πsi/2)

　＝2cos(πs/2)

ですから、

　2cos(πs/2)ζ(s)Γ(s)＝(2π)^sζ(1－s)　

よって

　ζ(1－s)＝2cos(πs/2)Γ(s)/ (2π)^s・ζ(s)

　　　　＝cos(πs/2)Γ(s)/ 2^s－1π^s・ζ(s)

が得られました。

＜2つの関数等式＞

オイラ－による関数等式（非対称型）

　ζ(1－s)=cos(sπ/2) Γ(s)ζ(s)／2^s－1π^s・・・・（1）

から、リ－マンによる関数等式（対称型）

　π^－s/2Γ(s/2)ζ(s)＝π^－(1－s)/2Γ((1－s)/2)ζ(1－s) ・・・・（2）

を導出します。

（2）式より

　ζ(1－s)＝π^－s/2Γ(s/2)ζ(s) π^(1－s)/2 /Γ((1－s)/2)

　　　　　＝π^－s+1/2Γ(s/2) /Γ((1－s)/2)・ζ(s)

より、

　　cos(sπ/2) Γ(s)／2^s－1π^s＝π^－s+1/2Γ(s/2) /Γ((1－s)/2)

すなわち

　　Γ((1－s)/2) Γ(s) cos(sπ/2)＝2^s－1π^1/2Γ(s/2)

が成り立つことを示します。

ガンマ関数の相反公式

　Γ(s)Γ(1－s)＝π/sin(πs)

でs→(1－s)/2に置き換えると、1－(1－s)/2＝(1＋s)/2より

　Γ((1－s)/2)Γ((1＋s)/2)＝π/sin(π(1－s)/2)

　Γ((1－s)/2)Γ((1＋s)/2)＝π/cos(πs/2)　　・・・（5）

が成り立ちます。

また、ルジャンドルの2倍公式

　Γ(2s)＝2^2s-1/π^1/2・Γ(s) Γ(s+1/2)

でs→s/2に置き換えると、

　Γ(s)＝2^s-1/π^1/2・Γ(s/2) Γ((s+1)/2) 　・・・（6）

が成り立ちます。

(5)、（6）式の辺々を掛け、Γ((s+1)/2)を消去すると

　Γ((1－s)/2)・Γ(s)＝π/cos(πs/2)・2^s－1/π^1/2・Γ(s/2)

すなわち

　Γ((1－s)/2) Γ(s) cos(sπ/2)＝2^s－1π^1/2Γ(s/2)

が成り立つことが示されました。関数等式はゼ－タ関数の定義域を拡大する場面でよく用いられす。

 

＜複素関数論からフーリエ変換を導く方法＞

　f(t)＝∫_{[－∞、∞]} F(ω) e^iωt dt

   F(ω)＝1/2π・∫_{[－∞、∞]} f(t) e^－iωt dt

 

＜コ－シ－の積分公式＞

F(z)が有限領域Dで正則であり、領域D内部の単一閉曲線Cz内の点zにおける値は、

　F(z)＝1/2πi・∫_Cz F(ξ)/(ξ－z) dξ

と表される。

 

F(z)をn回微分すると

　F⁽ⁿ⁾(z)＝n！／2πi・∫_Cz F(ξ)/(ξ－z) ⁿ⁺¹ dξ

となる。よってz＝0のとき

   F⁽ⁿ⁾(0)/ n！＝1/2πi・∫_C0 F(ξ)/ξⁿ⁺¹ dξ　・・・（1）

である。いま

   Σ_n＝Σ_{n＝－∞～∞}

と略記する。関数F(z)をｚ＝0の周りでローラン展開すると、F(z)は

　F(z)＝Σ_n F⁽ⁿ⁾(0)/ n！zⁿ

と表される。（1）式を代入すると

　F(z)＝Σ_n [1/2πi・∫_C0 F(ξ)/ξⁿ⁺¹ dξ] zⁿ・・・（2）

と書ける。

　e^{i2π(t＋T)/T}＝e^i2πt/T・e^i2π＝e^i2πt/T

であるから、関数f(t)を

　f(t)＝F( e^i2πt/T)　　・・・（3）

と定義すると、関数f(t)は

　f(t＋T)＝f(t)

により、周期Tの周期関数になる。（2）式を用いると

　f(t)＝Σ_n [1/2πi・∫_C0 F(ξ)/ξⁿ⁺¹ dξ] ( e^i2πt/T) ⁿ

　　＝Σ_n C _n ( e^i2πt/T) ⁿ

と書ける。いま、ξ＝e^i2πs/T によってξからsに変数変換する。

　dξ＝i2π/T・e^i2πs/T ds

s＝－T/2のとき、ξ＝e^{i2π(－T/2)/T}＝e^－iπ＝－1

s＝＋T/2のとき、ξ＝e^i2π(+T/2)/T＝e^+iπ＝－1

つまりξが半径1の円周C₀上を動くとき、sは－T/2からT/2に動くことに注意すると、

C _n＝1/2πi・∫_C0 F(ξ)/ξⁿ⁺¹ dξ

    ＝1/2πi・∫_{[－T/2、T/2]} F(e^i2πs/T)/ (e^i2πs/T)ⁿ⁺¹ 2πi /T・e^i2πs/T ds

　＝1/T∫_{[－T/2、T/2]} F(e^i2πs/T)/ (e^i2πs/T)ⁿ⁺¹・e^i2πs/T ds

　＝1/T∫_{[－T/2、T/2]} F(e^i2πs/T) (e^i2πs/T)^－n ds

　＝1/T∫_{[－T/2、T/2]} f(s)e^－i2πsn/T ds

となる。

　ω_n＝2πn/T

とおくと、

　Δω＝ω_n+1－ω_n＝2π/T → 0　as  T → ∞

　1/T＝Δω/2π

なので、

f(t)＝Σ_n C _n e^{iωn t}

　 ＝∫ _{[－∞、∞]} dω[∫_{[－T/2、T/2]} f(s)e^－iωs ds] e^iωt

    ＝∫ _{[－∞、∞]} dω[1/2π∫_{[－∞、∞]} f(s)e^－iωs ds] e^iωt

    ＝∫ _{[－∞、∞]} F(ω) e^iωt dω

F(ω)＝1/2π∫_{[－∞、∞]} f(s)e^－iωs ds

が示された。

  ＜テータ関数の変換公式＞

ｓ＞0のとき

　θ(s)＝Σ_{n＝－∞～∞}exp(－πsn²)

に対して、

　θ(1/s)＝√s・θ(s)

が成り立つ。

[証明]　関数f(t)を

　f(t)＝exp(－πst²)

とおくと、

　θ(n)＝Σ_{n＝－∞～∞}f(n)

である。f(t)のフーリエ変換をF(m)とすると

　F(m)＝∫_{[－∞、∞]} exp(－πst²)e^－i2πmt dt

である。これをｍで一回微分すると

　d F(m)/dm＝∫_{[－∞、∞]} exp(－πst²) (－i2πt)e^－i2πmt dt

　　　　　  ＝i/s・∫_{[－∞、∞]} (－2πst)exp(－πst²) e^－i2πmt dt

                    ＝i/s・∫_{[－∞、∞]} (d/dt)exp(－πst²) e^－i2πmt dt

                  ＝i/s・[exp(－πst²) e^－i2πmt]t=_－∞、∞－i/s∫_{[－∞、∞]} exp(－πst²) (－i2πm) e^－i2πmt dt

　　　　   ＝－2πm/s・∫_{[－∞、∞]} exp(－πst²) e^－i2πmt dt

　　　　   ＝－2πm/s・F(m)

となる。微分方程式を解くと

　[logF(m)]’＝F’(m)/ F(m)＝－2πm/s
    logF(m)＝－πm²/s

を解いて、
   F(m)＝F(0)exp(－πm²/s)

が得られる。

　F(0)＝∫_{[－∞、∞]} exp(－πst²) dt

ここで、u＝√(πs)・t　と置くと

　F(0)＝1/√(πs)∫_{[－∞、∞]} exp(－u²) du

　　　＝1/√(πs)・√π　＝1/√s

従って、フ－リエ変換後の関数は

　　F(m)＝1/√s ・exp(－πm²/s)

となる。ここで

f(t)＝exp(－πst²)　は[－∞、∞]区間上の連続関数であるから、Poissonの和公式より

　Σ_n f(n)＝Σ_n F(n)

すなわち

　Σ_n exp(－πsn²)＝Σ_n 1/√s ・exp(－πn²/s)

が成り立つ。いま、θ(s)＝Σ_{n＝－∞～∞}exp(－πsn²)　より

　θ(s)＝1/√s ・θ(1/s)

が成り立つことが示された。

 

[補題]　正の実数xに対して、

　Σ_n exp[－π(n＋α)²/x]＝√x Σ_n exp[－πn²x＋ i2πnα]

が成り立つ。

・α＝0を代入すると、θ(1/x)＝√x ・θ(x)　が成り立つ。

[証明]　

  f_αx(y)＝exp[－π(y＋α)²/x]

とおいて、

  Σ_n f_αx(y)＝√x Σ_n exp[－πn²x＋ i2πnα]

を示す。Poissonの和公式より

　Σ_n f_αx(n)＝Σ_n∫_{[－∞、∞]} f_αx(y) e^－i2πny dy

＝Σ_n ∫_{[－∞、∞]} exp[－π(y＋α)²/x] e^－i2πny dy

ここで、y+α＝xuとおくと、

  Σ_n f_αx(n)＝Σ_n∫_{[－∞、∞]} exp[－πxu²] e^{－i2πn(xu－α)} dy

                 ＝Σ_n e^i2πnα∫_{[－∞、∞]} exp[－πxu²] e^－i2πnxu xdu

ここで

    －πxu²－i2πnxu＝－πx(u²＋i2nu)＝－πx(u＋in) ²－πxn ²

であるから、

     Σ_nf_αx(n)＝xΣ_ne^i2πnαexp[－πxn ²]∫_{[－∞、∞]} exp[－πx(u＋in)²] du　　

　　　　　  ＝xΣ_ne^i2πnαexp[－πxn ²]・lim_N→∞ I(N)

ここで
    I(N)＝∫_[－N、N] exp[－πx(u＋in)²] du＝∫_Aexp[－πx(u＋in)²] du　　

とした。この積分の経路は複素平面で、

  A：z＝u＋in（－N≦u≦N）

である。コーシ－の定理より、非積分関数は正則関数なので、経路A上の複素積分を以下のB→C→Dに変えることができる。

   I(N)＝∫_B→C→D exp[－πx(z)²] dz　　

において

　B：z＝－N+it、0≦t≦n

　C：z＝t、－N≦t≦N

　D：z＝N+it、0≦t≦n

経路Bでの積分は

　I_B(N)＝∫_[n、0] exp[－πx(－N＋it)²] dt　　

          ＝－exp[－πxN²]∫_[0、n] exp[(1－it/N)²] dt　

ここでt’＝t/N　とおくと、

  I_B(N)＝∫_[0、n] exp[(1－it/N)²] dt

       ＝1/N・∫_[0、n/N] exp[(1－it’)²] dt’　→ 0　as　N→∞

となり、N→∞での積分値はゼロになる。

同様に経路Dでの積分は

   I_D(N)＝∫_[0、N] exp[－πx(N＋it)²] dt

          ＝1/N・∫_[0、n/N] exp[(1＋it’)²] dt’　→ 0　as　N→∞

となり、N→∞での積分値はゼロになる。経路Cでの積分は

   I_C(N)＝∫_[－N、N] exp[－πxt²] dt　　

　　　＝1/√(πx) ・∫_[－N、N] exp[－t²] dt　→　√π/√(πx)＝1/√x　as　N→∞

となり、N→∞での積分値は1/√xとなる。

従って

　lim_N→∞ I(N)＝lim_N→∞｛I_B(N)＋I_C(N)＋I_D(N)｝＝1/√x　

を得る。結局

  Σ_n f_αx(n)＝x Σ_ne^i2πnαexp[－πxn ²]・lim_N→∞ I(N)

　　　　＝x Σ_ne^i2πnαexp[－πxn ²] 1/√x
              ＝√x・Σ_nexp[－πxn ²＋i2πnα]

が成り立つことが示された。

＜Poissonの和公式＞

[－∞、∞]区間上の任意の連続関数f(x)とそれをフーリエ変換した関数

　F(n)＝∫_{[－∞、∞]} f(t)e^－i2πnt dt

に対して、

　Σ_{n＝－∞～∞} f(n)＝Σ_{n＝－∞～∞} F(n)

が成り立つ。

[証明]　 連続関数f(t)に対して

　g(t)＝Σ_{n＝－∞～∞}f(n+t)

を定義する。

　g(0)＝Σ_{n＝－∞～∞}f(n)

であり、g(t)は

　g(t+1)＝g(t)

なる周期性を持つので、フ－リエ級数展開

　g(t)＝Σ_{n＝－∞～∞}c_n e^i2πnt

ができる。t=0のとき

　g(0)＝Σ_{n＝－∞～∞}c_n

が成り立つ。一方、

　F(m)＝Σ_{n＝－∞～∞}∫_[n、n+1] f(t)e^－i2πmt dt

　　　＝Σ_{n＝－∞～∞}∫_[0、1] f(t+n)e^{－i2πm(t+n)} dt

　　　＝∫_[0、1] [Σ_{n＝－∞～∞}f(t+n)] e^－i2πmt dt

　　　＝∫_[0、1] g(t) e^－i2πmt dt

　　　＝∫_[0、1] [Σ_{n＝－∞～∞}c_n e^i2πnt] e^－i2πmt dt

　　　＝Σ_{n＝－∞～∞}c_n・[∫_[0、1] e^i2π(n－m)t dt]

　　　＝Σ_{n＝－∞～∞}c_n・δ_nm

　　　＝c_m

従って

　g(0)＝Σ_{n＝－∞～∞}f(n)＝Σ_{n＝－∞～∞} F(m)

が成り立つ。

 

ディリクレ積分

　∫_[0,∞] sin(x) /x dx＝π/2　

を複素積分

　∫_C e^iz /z dz＝0

で求めます。

閉積分経路Cを

　C＝C₁＋C₂＋C₃＋C₄

に分けます。ここで

　C₁：z＝Re^iθ0≦θ≦π

　C₂：z＝x　–R≦x≦－δ

　C₃：z＝δe^iθ0≦θ≦π

　C₄：z＝x　δ≦x≦R

とします。閉積分経路C内にz=0の極は含まれないので、Cでの積分はコーシ－の定理よりゼロになります。

（1）C₁の積分

　0≦sinθ≦1　かつ　2θ/π≦sinθ（0≦θ≦π）、

ですから、

　｜exp(iRe^iθ)｜＝｜exp{iR(cosθ+ i sinθ)}｜

　　　　　　　＝｜exp{iRcosθ}・exp{－R sinθ)}]｜

　　　　　　　＝e^{－R sinθ}

　　　　　　　≦e^－R2θ/π

従って

　｜∫_C1 e^iz /z dz｜＝｜∫_[0，π]  exp(iRe^iθ) /Re^iθ ・iRe^iθdθ｜

　　　　　　　　 ≦∫_[0，π] e^－R2θ/πdθ

　　　　　　　　 ＝－π/2R・[e^－R2θ/π] _θ＝0，π

＝π/2R・(1－e^－2R)　→　0　as　R→∞

C₁の積分はRが無限大になるとゼロになります。

（2）C₂の積分

ここで　x’＝‐xに置き換えると

　∫_C2 e^iz /z dz＝∫_[R，δ] e^‐ix’ /x’ dx’＝－∫_[δ、R] e^‐ix’ /x’ dx’

となります。

（3）C₃の積分

　　∫_C3 e^iz /z dz＝∫_[π，0]  exp(iδe^iθ) /δe^iθ ・iδe^iθdθ

　＝i∫_[π，0]  {1+(iδe^iθ)+O(δ²)｝dθ

　→　i∫_[π，0] dθ＝－iπ　as　δ→0

（4）C₄の積分

　∫_C3 e^iz /z dz＝∫_[δ、R] e^ix /x dx

となります。以上より

0＝∫_C1 e^iz /z dz＋∫_C2 e^iz /z dz＋∫_C3 e^iz /z dz＋∫_C4 e^iz /z dz

　　＝∫_CRe^iz /z dz－∫_[δ、R] e‐^ix /x dx＋∫_[δ、R] e^ix /x dx－iπ

　　＝∫_CRe^iz /z dz ＋∫_[δ、R](e^ix－e^‐ix) /x dx－iπ

　　＝∫_CRe^iz /z dz ＋2i∫_[δ、R]sin(x) /x dx－iπ

ここで　δ→0かつR→∞　とすると

　2i∫_[0、∞]sin(x) /x dx－iπ＝0

すなわち

　∫_[0、∞]sin(x) /x dx＝π/2

が得られます。複素積分を用いると簡単にディリクレ積分の値が求められました。

ペーター・グスタフ・ディリクレ（Peter Gustav Dirichlet, 1805年～1859年）はフランス生まれのドイツ人数学者です。ディリクレは現代的な関数概念（写像）を与えたことで知られています。家族の名前Dirichletは祖父がベルギ-のリシュレの街の出身だったことに由来しています。ペータ－はガウスの「整数論」を持ってフランスへ行き、パリ大学などで、フ－リエ（指導教官）、ラプラス、ルジャンドルらから数論と解析学を学びます。ペータ－は22歳の時にドイツに戻り、10年間ベルリン大学に滞在し、レベッカ・メンデルスゾーンと結婚します。妻のお兄さんは有名な作曲家で、彼の家は絶えず賑やかだったそうです。ディリクレは1855年からガウスの後継として、ゲッティンゲン大学で教授を務めます。友達の数学者にカ－ル・グスタフ・ヤコビがいます。彼の教え子たちにはアイゼンシュタイン、リーマン、クロネッカー、リプシッツがいます。友人の数学者リヒャルト・デ‐デキントが彼の研究結果をまとめて『整数論講義』を出版しました。ディリクレの名前が付けられた定理は、数論や解析学で数多く出てきます。ディリクレの積分定理は師匠のフーリエ変換の数学的基礎づけを行うためのものです。

＜ディリクレの積分定理＞

区分的に滑らかな関数f(x)に関して

　Lim _λ→∞∫_[－a,－a] f(x)sin(λx)／x dx＝π/2・[f(+0)＋f(－0)]

が成り立つ。ここで

　f(+0)＝Lim _x→0 f(x)  for　x＞0

　f(－0)＝Lim _x→0 f(x)  for　x＜0

のことです。f(x)がx＝0で連続ならば、

　Lim _λ→∞∫_[－a,－a] f(x)sin(λx)／x dx＝π・f(0)

となります。「区分的に滑らか」とは積分区間で有限個の有限な不連続点があり、その間は1回微分可能であることを意味しています。

[証明]

I(λ)＝∫_[b,ｃ] f(x)sin(λx) dx

とおくと、

　Lim _λ→∞ I(λ)＝0　　・・・（1）

が成り立ちます。（1）式は後で証明します。一方

　∫_[0,∞] sin(λx) /x dx＝π/2　（λ＞0）　・・・（2）

が成り立ちます。この積分をディリクレ積分と呼びます。ディリクレ積分は収束しますが、絶対収束しない積分として有名です。（2）式も後で証明します。

I(λ)において、f(x)→{f(x)－f(+0)}／x と置き換えると、

　　f’(0)＝Lim _x→0{f(x)－f(+0)}／x

は存在しているので、

　∫_[0,a] {f(x)－f(+0)}／x ・sin(λx) dx＋∫_[－a,0] {f(x)－f(+0)}／x ・sin(λx) dx　→0　λ→∞

が成り立ちます。すなわち

　∫_[－a,a] f(x) sin(λx)／x dx＝f(+0)∫_[0,a] sin(λx)／x dx＋f(－0)∫_[－a,0] sin(λx)／x dx

x’＝－x　とおくと

　∫_[－a,0] sin(λx)／x dx＝－∫_[＋a,0] sin(λx’)／x’ dx’＝∫_[0,a] sin(λx)／x dx

であるから、

　∫_[－a,a] f(x) sin(λx)／x dx＝[f(+0)＋f(－0)]・∫_[0,a] sin(λx)／x dx

となります。a→∞をとると、（2）式より

　∫_[－∞,∞] f(x) sin(λx)／x dx＝[f(+0)＋f(－0)]・π/2

が得られます。

f(x)＝1のとき、x’＝λxとおくと

　∫_[－∞,∞] sin(λx)／x dx＝∫_[－∞,∞] sin(x’)／x’ dx’＝π/2

が成り立ちます。

次に（1）式の証明を行います。x＝y＋π/λ　とします。

　　Sin(λ(y＋π/λ))＝sin(λy＋π)＝－sin(λy)

　I(λ)＝－∫_{[b－π/λ、c－π/λ]} f(y＋π/λ) sin(λy)dy・・・（3）

となります。

　I(λ)＝∫_[b,c] f(x)sin(λx) dx・・・（4）

(3)＋(4)を行うと、積分区間を

　　[b －π/λ、c]＝[b－π/λ、b]＋[b、c－π/λ]＋[c－π/λ、c]

に分割できるので、

　2 I(λ)＝－∫_{[b－π/λ、b]} f(x＋π/λ)sin(λx) dx＋∫_{[b、c－π/λ]} [ f(x)－f(x＋π/λ)]sin(λx) dx

　　　　　＋∫_{[c－π/λ、c]} f(x)sin(λx) dx

となります。ワイエルシュトラスの最大値定理より、閉区間[b、c]において、最大値M＞0が存在して

　｜f(x) sin(λx)｜≦｜f(x)｜≦M　となるので、

　2｜I(λ)｜≦2Mπ/λ＋∫_{[b、c－π/λ]} ｜f(x)－f(x＋π/λ)｜dx　＜2ε

となります。任意のε＞0に対して、λ＞0が存在して、

　　2Mπ/λ＜ε　　かつ　　｜f(x)－f(x＋π/λ)｜＜ε/(c－b)

が成り立ちます。従って

　　lim_λ→∞｜I(λ)｜＝0　

が示されました。

＜フーリエの積分定理＞

区分的に滑らかな関数f(t)に対して

　　F(ω)＝∫_{[－∞、∞]}f(t)e^－iωtdt

が存在し、

　　1/2π・∫_{[－∞、∞]} F(ω) e^－iωtdω＝1/2・[f(t＋0)＋f(t－0)]

が成り立つ。

証明)　ディリクレの積分定理より、区分的に滑らかな関数f(x)に関して

　Lim_λ→∞∫_[－a,－a] f(τ)sin(λτ)／τ dτ＝π/2・[f(+0)＋f(－0)]

が成り立ちます。いま、f(τ)をf(τ+t)と置き換え、a→∞とすると

　Lim_λ→∞∫_{[－∞,－∞]} f(τ+ｔ)sin(λτ)／τ dτ＝π/2・[f(t+0)＋f(t－0)]

t’＝τ+ｔと変数変換すると

　左辺＝Lim_λ→∞∫_{[－∞,－∞]} f(t’)sin(λ(t’－t))／(t’－t) dt’

となります。

　∫_[0,λ] cosω (t’－t)dω＝[sin(ω(t’－t))／(t’－t)]_ω＝0、λ＝sin(λ(t’－t))／(t’－t)

ですから、これを代入すると

　左辺＝Lim_λ→∞∫_{[－∞,－∞]} f(t’) [∫_[0,λ] cosω (t’－t)dω] dt’

となる。ここで

　cosω (t’－t)＝1/2(e^{iω (t’－t)}＋e ^{－iω (t’－t)})

です。ω’＝－ωと置くと

　∫_[0,∞] e^{iω (t’－t)} dω＝－∫_[0,－∞] e^{－iω’ (t’－t)} dω’＝ ∫_[－∞,0] e^{－iω (t’－t)} dω

となります。

左辺＝1/2∫_{[－∞,－∞]} f(t’) [∫_[0,∞] e^{iω (t’－t)}dω＋∫_[－∞,0] e^{－iω (t’－t)}dω] dt’

　　＝1/2∫_{[－∞,－∞]} f(t’) [∫_[－∞,∞] e^{－iω (t’－t)}dω] dt’

　　＝1/2∫_{[－∞,－∞]} [∫_[－∞,∞] f(t’) e^－iωt’ dt’ ] e^iωt dω

が得られます。よって

　F(ω)＝∫_[－∞,∞] f(t) e^－iωt dt

とおくと、

　1/2π・∫_{[－∞,－∞]} F(ω)e^iωt dω ＝1/2・[f(t+0)＋f(t－0)]

が示されました。

ディリクレ積分

　　∫_[0,∞] sin(λx) /x dx＝π/2　（λ＞0）　・・・（2）

は収束しますが、

　∫_[0,∞] ｜sin(x) /x｜dx＝Σ_k=1～∞∫_{[(k－1)π、kπ]} ｜sin(x)｜/x dx

　　　　　　　　　　　≧Σ_k=1～∞∫_{[(k－1)π、kπ]} ｜sin(x)｜/kπ dx

　　　　　　　　　　　＝1/π・Σ_k=1～∞1/k∫_[0、π] sin(x)dx

　　　　　　　　　　　＝2/π・Σ_k=1～∞1/k　＝∞

によって絶対収束しません。

命題1　

　∫_[0、∞] e^－axsin(x) /x dx＝π/2－tan^－1(a)　a＞0

が成り立つ。

部分積分をすると、

I(a)＝∫_[0、∞] e^－axsin(x) dx＝－[e^－axcos(x)]_x＝0～∞＋∫_[0、∞] (－a)e^－axcos(x) dx＝

　　　＝1－a｛[e^－axsin(x)] _x＝0～∞－(－a)∫_[0、∞] e^－axsin(x) dx｝

　　　＝1－a²I(a)

　I(a)＝1/(1＋a²)

となります。

　　∫_[∞、a’] I(a)da＝∫_[∞、a’]∫_[0、∞] e^－axsin(x) dx da

　＝∫_[0、∞] [∫_[∞、a’] e^－ax da] e^－ax da sin(x) dx

ここで

　　∫_[∞、a’] e^－ax da＝－1/x・[e^－ax]_{a＝∞～a’}＝ －1/x・e^－a’x

であるから、

　∫_[0、a’] I(a)da＝－∫_[0、∞] e^－a’x sin(x)/x dx

一方、

∫_[∞、a’] I(a)da＝∫_[∞、a’] 1/(1＋a²)da

a=tanθ-とおくと、1/(1+tan²θ)=cos²θ、da=1/ cos²θdθ

a：∞→a’、 θ：π/2→tan^－1(a’) より

∫_[∞、a’] I(a)da＝∫_{[π/2、tan－1(a’)]} 1da＝tan^－1(a’)－π/2＝－∫_[0、∞] e^－a’x sin(x)/x dx

である。従って

　∫_[0、∞] e^－ax sin(x)/x dx＝π/2－tan^－1(a)

が示された。

上式でa=0のとき

　I(0)＝∫_[0,∞] sin(x) /x dx＝π/2　

が成り立ちます。上式は複素積分で示すこともできます。

ゼ－タ関数は

　ζ(z)＝∑_k=1～∞1/k^z＝1＋1/2^z＋1/3^z＋1/4^z＋・・・　　　Re(z)＞1

という複素関数です。ゼ－タ関数の零点とは、ζ(z)＝0となるｚのことです。今回はゼ－タ関数の零点を計算してみました。前回、ゼ－タ関数は

　ζ(z)＝∏_p(1/[1－1/p^z])＝1／[1－1/2^z]・[1－1/3^z]・[1－1/5^z]・[1－1/7^z]・・・

のように素数の積で表示できることを示しました。このことが示唆するように、ゼ－タ関数の零点と素数には密接な関係があることが知られています。

前回、イ－タ関数η(z)　（前回はη(z)をL(z)と書きました。）

　η(z)＝∑_k=1～∞(－1)^k－1/k^z＝1－1/2^z＋1/3^z－1/4^z＋1/5^z－1/7^z＋・・・          Re(z)＞0

を使うと、ゼ－タ関数

　ζ(z)＝η(z)/(1－2^1－z)　　Re(z)＞0　ｚ≠1

の定義域は、Re(z)＞0に拡大できることを示しました。ゼ－タ関数は、ガンマ関数を用いて表示することでRe(z)＜0にも拡大できます。ゼ－タ関数の零点には、ｚ＝－2、－4、－6・・・・に自明な零点があることが分かっています。1859年にリ－マンはゼ－タ関数の非自明な零点はRe(z)＝1/2の線上に分布すると予想しました。今回は

　ζ(z)＝η(z)/(1－2^1－z)＝0

を満たす非自明な零点の分布を調べて見ました。問題は、無限和を有限和で置き換えると、級数の収束が遅いので、誤差が大きくなってしまうことです。私のパソコンでは、10万項の級数を計算しても、Re(z)＝1/2の線上の零点の虚数座標を有効数字4桁の精度（t₁＝14.13）でしか求められませんでした。そこでクノップ変換を行い級数の収束性を高めました。　N＝40（40×40/2＝800項）の計算で零点を有効数字7桁の精度（t₁＝14.13473）で求めることができました。マンゴルトの明示公式の周期項を微分して得た素数スペクトル曲線に12個の零点を入れて9個の素数を再現しました。

クノップ変換では。収束が遅い級数に「1に収束する級数」を挿入して和の順番を変えることで、級数の収束性を高めます。パラメータｑの値を変えることで、収束速度と収束領域が変わります。

関数b(k,N)はNが無限大になると1になりますが、Nが有限だと、ｋがN/2より大きい所では1より小さくなります。　コンラッド・クノップ(1882～1957)は無限級数の収束を研究したドイツ人の数学者です。

 

[12]素数定理の証明手順のまとめ

[０]関数の定義　P；素数の集合

・リーマンのゼ－タ－関数：ζ(s)＝Σ_{[n＝1～∞]} 1/n^s、Re(s)＞1

　（nに関する無限級数）

・ファイ関数：Φ(s)＝Σ_[p∊P] log(p)／p^s、Re(s)＞1

　（すべての素数に関する和をとる）

・チェビシェフのシータ関数：θ(x)＝Σ_[p≦x] log(p)

  （X以下の素数pに関する和をとる）

・素数の個数関数：π(x)＝Σ_[p≦x]1

[Ⅰ]命題1　Re(s)＞1、ζ(s)＝Π_[p∊P] [1／(1－1/p^s)]　オイラ－積表示の存在

（1）Re(s)＞1でζ(s)のディリクレ級数表示は収束する。

（2）ζ(s)のディリクレ級数表示はオイラ－積表示に一致する。

（3）Re(s)＞1でζ(s)のオイラ－積表示は収束する。

（4）ζ(s)は、s＞0（s≠1）に拡張することができる。

[Ⅱ] 命題2　ζ(s)－1/(ｓ－1)はRe(s)＞0で正則である。

（1）∫_[1,∞]1/x^s dx＝1/(s‐1)　for　s＞1

（2）s∫_[n,x] 1/t^s+1 dt＝1/n^s－1/x^s

（3）｜t^s+1｜＝t^Re(s)+1

（4）ζ(s)－1/(ｓ－1)≦｜s｜ζ( Re(s)+1) for　s＞1　

[Ⅲ] 命題3　Φ(s)－1/(ｓ－1)はRe(s)≧1で正則である。

（1）ζ’(s)/ζ(s) ＋1/(s－1)　はRe(s)≧1で正則である。

（2）Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)＋1/(s‐1)]－Σ[p] log(p)／p^s(p^s‐1) 　を示す。

（3）右辺2項目Σ[p] log(p)／p^s(p^s‐1)はRe(s)＞1/2で正則である。

（4）Re(s)＝1でζ(s)＝0なる零点が存在しない。

[Ⅳ] 命題4　θ(x)＝Ｏ(x)　i.e.　∃ｋ＞0　｜θ(x)｜≦ｋx

（1）2nlog2≧θ(2n)－θ(n)

（2）2^ｍ+1・log2＞θ(2^m)

  (3) θ(x) ≦4log2・x

[Ⅴ] 命題5　∫_[1，∞] [θ(x)－x]／x² dxは収束する。

・[Ⅲ] 、[Ⅳ]、[定理A]を用いて証明する。

（1）Φ(s)＝s∫_[1，∞] θ(x)／x^ｓ+1dx、Re(s)＞1

（2）f(t)＝θ(e^t)e^－t－1　（t≧0）は有界、g(z)＝∫_[0，∞] f(t)exp[－zt] dtが存在する

（3）g(z)＝Φ(z+1)／(z+1)－1/z　　Re(z)＞0

（4）g(z)はRe(z)≧0で正則

（5）g(0)＝∫_[0，∞] f(t) dt＝∫_[1，∞] [θ(x)－x]／x² dx　が収束する。

[Ⅵ] 命題6　θ(x)～x　i.e.　lim_[x→∞] θ(x)/x＝1

・任意のε＞0、∃x＞0　1－ε＜θ(x)/x＜1＋εを示す。

・背理法を用いて矛盾を示す。任意の正数ｘに対して、∃ε＞0

（1）1＋ε≦θ(x)/x　は矛盾を生じるので、θ(x)/x＜1＋ε　by [Ⅴ]

（2）θ(x)/x≦1－ε　は矛盾を生じるので、1－ε＜θ(x)/x 　by [Ⅴ]

[Ⅶ] 素数定理　Lim _[x→∞] π(x) logx／x＝1

（1）1←θ(x)/x≦π(x)log(x)/x　by [Ⅵ]

（2）π(x)log(x)/x≦1/(1－ε)・θ(x)/x＋log(x)/x^ε→1/(1－ε)　→1

[定理A]　Newmanの解析定理

t≧0で有界かつ可積分な関数f(t)に対して、

g(z)＝∫_[0，∞] f(t)exp[－zt] dt　Re(z)＞0

がRe(z)≧0で正則であれば、

　g(0)＝∫_[0，∞] f(t) dt

が存在する。つまり正則関数

　g_T(z)＝∫_[0，T] f(t)exp[－zt] dt

に対して、

　lim_[T→∞]g_T(0)＝g(0)

が存在する。

[定理A]　Newmanの解析定理の証明手順

（1）g(0)－g_T(0)＝1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz

（2）A＝｜g(0)－g_T(0)｜＝｜1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz｜

　　　≦A₊＋A_－≦A₊＋A_－1＋A_－2 → 2B/R（T→∞）→ 0 （R→∞）

（3）A₊≦B/R、Re(z)＞0　

（4）A_－1＝｜1/2πi・∫_C－g_T(z)e^zT(1＋z²/R²)／z dz｜≦B/R　

（5）A_－2＝｜1/2πi・∫_C－g(z)e^zT(1＋z²/R²)／z dz｜→ 0

[Ⅷ]　Newmanの解析定理の証明

（1）g(0)－g_T(0)＝1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz を示します。

コ－シ－の積分公式より、領域Dで正則な複素関数f(z)のD内の閉曲線C上の積分に関して、

閉曲線Cで囲まれた領域の点αにおいて

• f(α)＝1/2πi・∫_C f(z)／(z－α) dz

が成り立つ。閉曲線Cの半径R＞0として、

• f(z)＝[g(z)－g_T(z)]e^zT(1＋z²/R²)

を考えると、f(z)は以下で定義される領域Dで正則であることが分かります。

任意の閉曲線C上のg_T(z)の積分は、∫_C e^－ztdz＝0より

• ∫_C g_T(z)dz＝∫_C (∫_[0,T]f(t)e^－ztdt)dz＝∫_[0,T] f(t) (∫_C e^－ztdz)dt＝0

です。モレラの定理から、g_T(z)は任意の閉曲線C内で正則です。解析定理の前提より、g(z)はRe(z)≧0で正則なので、Re(z)＝0上の任意の点z＝it（－∞≦t≦∞）でテ－ラ－展開でき、その収束円内のzでも正則です。従って、十分大きなR＞0と十分小さなδ＞0において、「｜z｜≦R　かつ－δ≦Re(z)」となる領域Dの境界線を閉曲線Cとすると、閉曲線Cの内部領域Dでg(z)とg_T(z)は正則です。e^zT(1＋z²/R²)も正則なので、f(z)は正則関数となり、

コ－シ－の積分公式を適用できます。いまz＝0で

• f(0)＝g(0)－g_T(0)

です。α＝0として、コ－シ－の積分公式を適用すると

• f(0)＝g(0)－g_T(0)＝1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz

が成り立ちます。

（2）A＝｜g(0)－g_T(0)｜＝｜1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz｜

　　　≦A₊＋A_－≦A₊＋A_－1＋A_－2 → 2B/R（T→∞）→ 0 （R→∞）

を示します。そのために、積分路を

• C＝C₊ (Re(z)＞0)＋C_－(Re(z)＜0)

に分け、

　A₊＝｜1/2πi・∫_C+ [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz｜

　A_－＝｜1/2πi・∫_C－[g(z)－g_T(z)] e^zT(1＋z²/R²)／z dz｜≦ A_－1＋A_－2

とします。ここで

　A_－1＝｜1/2πi・∫_C－’g_T(z)e^zT(1＋z²/R²)／z dz｜

　A_－2＝｜1/2πi・∫_C－g(z)e^zT(1＋z²/R²)／z dz｜

とします。これから

　A≦A₊＋A_－≦A₊＋A_－1＋A_－2 → 2B/R（T→∞）→ 0 （R→∞）

を示します。

 

 

 

 

 

 

 

（3）A₊≦B/R、Re(z)＞0　を示します。

z＝Re^iθとおいて積分変数をzからθに変換すると、dz＝i Re^iθdθ

　　A₊≦1/2π｜∫_C＋｜g(z)－g_T(z)｜e^Re(z)T [1＋z²/R²]／z dz｜

非積分関数

[1＋z²/R²]／z＝[1＋R²e^2iθ/R²]/Re^iθ＝2[R(e^iθ＋e^－iθ)/2]/R²＝2Re(z) /R²

より

　　A₊≦1/2π∫_C＋｜g(z)－g_T(z)｜e^Re(z)T2Re(z) /R²｜dz｜

いま、｜f(t)｜≦B（有界）なので

｜g(z)－g_T(z)｜＝｜∫_[T，∞] f(t)exp[－zt] dt｜≦B｜∫_[T，∞] exp[－Re(z)t] dt｜

　　　　　　＝－B/ Re(z)[ exp[－Re(z)t]]_t＝T,∞＝B/ Re(z)・e^－Re(z)T

です。従って、

A₊≦1/2π∫_C＋B/ Re(z)・e^－Re(z)T・e^Re(z)T2Re(z) /R²｜dz｜＝(B/πR²) ∫_C＋｜dz｜

となります。∫_C＋｜dz｜＝πRより

　　A₊≦B/R

が得られます。

（4）A_－1＝｜1/2πi・∫_C－g_T(z)e^zT(1＋z²/R²)／z dz｜≦B/R　を示します。

Re(z)＜0より、C- ’の積分経路を用いる。｜Re(z)｜＝－Re(z)に注意して

　｜g_T(z)｜＝｜∫_[0，T] f(t)e^－zt dt｜≦B∫_[0，T] e^－Re(z)t dt＝B/(－Re(z))[e^－Re(z)t]t=0,T

　　　　　＝B/(－Re(z))[e^－Re(z)T－1]≦B/(－Re(z))e^－Re(z)T

　A_－1＝｜1/2πi・∫_C－’g_T(z)e^zT(1＋z²/R²)／z dz｜

　　　≦1/2π・∫_C－’｜g_T(z)｜e^Re(z)T｜(1＋z²/R²)／z｜｜dz｜

　　　≦1/2π・[B/(－Re(z))e^－Re(z)T] e^Re(z)T[2Re(z) /R²]・∫_C－’｜dz｜

　　　　＝1/2π・B/(－Re(z)) [2｜Re(z)｜/R²]・πR＝B/R

（5）A_－2＝｜1/2πi・∫_C－g(z)e^zT(1＋z²/R²)／z dz｜→ 0 as T→∞　を示す。

有界閉集合C－上のTを含まない複素関数の絶対値には最大値があり、

　｜g(z) (1＋z²/R²)/z｜≦M

なる正数Mが存在します。

　　A_－2≦M/2π・｜∫_C－e^zT dz｜≦M/2π・∫_C－e^Re(z)T｜dz｜

となる。C－上の積分路を弧AB上と直線BC上の2つに分けて、実行します。

1）弧AB上：z＝R e^iθ　(π/2≦θ≦λ)、cos(λ)＝－δ/R　｜dz｜＝Rdθ

2）直線BC上：z＝－δ＋it　(0≦t≦√(R²－δ²))　 ｜dz｜＝dt

実軸に対する対称性から、積分経路をIm(z)≧0に限定して、積分値を2倍します。

A_－2≦2・M/2π・[∫_AB e^Re(z)T｜dz｜＋∫_BC e^Re(z)T｜dz｜]

　　＝M/π・[∫_{[(π/2≦θ≦λ]} e^Rcos(θ)T Rdθ －∫_{[0≦t≦√(R2－δ2)]} e^－δT dt ]

t=cos(θ)とおくと、dt＝－sin(θ)dθ＝－√(1－t²) dθより、t：0→cos(λ)＝－δ/R

　＝M/π・[－∫_{[(0≦t≦－δ/R]} e^RTt R／√(1－t²) dt －√(R²－δ²)・e^－δT ]

　≦M/π・[－∫_{[(0≦t≦－δ/R]} e^RTt R／√(1－(δ/R)²) dt －√(R²－δ²)・e^－δT ]

　　＝M/π・[－R²／√(R²－δ²)・∫_{[(0≦t≦－δ/R]} e^RTt dt －√(R²－δ²)・e^－δT ]

ここで

　∫_{[(0≦t≦－δ/R]} e^RTt dt＝1/RT・[e^RTt]_{t＝0, －δ/R}＝1/RT・[e^－Tδ－1]

ですから、δ＞0より、

A_－2≦M/π・[R²／√(R²－δ²)・1/RT・[1－e^－Tδ]－√(R²－δ²)・e^－δT ] → 0 as T→∞

が得られます。

（3）～（5）より、

　　｜g(0)－g_T(0)｜＝A≦A₊＋A_－≦2B/R → 0  as  T→∞, R→∞

が成り立ちます。よって

　lim_[T→∞]g_T(0)＝g(0)

が存在することが証明されました。

 

＜コ－シ－の積分公式＞

領域Dで正則な複素関数f(z)のD内の閉曲線C上の積分に関して、Cで囲まれた領域の点z＝αにおいて

• f(α)＝1/2πi・∫_C f(z)／(z－α) dz

が成り立つ。Cの向きは反時計回りを正とする。

証明）z＝αの近傍で、正則関数f(z)を

• f(z)＝f(α＋z－α)＝f(α)＋f’(α) (z－α)＋1/2・f’’(α) (z－α)²＋・・・

と展開すると、正則関数1，z、z²、z³、・・は閉曲線C内に極をもたないので、コーシ－の積分定理よりC上の積分でゼロになります。

∫_C f(z)／(z－α) dz＝∫_C[f(α)＋f’(α) (z－α)＋1/2・f’’(α) (z－α)²＋・]／(z－α) dz

　＝f(α)・∫_C 1/(z－α) dz ＋f’(α)∫_C dz＋1/2・f’’(α) ∫_C (z－α) dz＋・・・

　＝f(α)・∫_C 1/(z－α) dz

となります。z＝α+e^iθとおくとdz＝ie^iθdθ、θ＝0～2πより

　∫_C 1/(z－α) dz＝∫_{[0≦θ≦2π]}i e^iθ/e^iθdθ＝2πi

従って

　∫_C f(z)／(z－α) dz＝2πi f(α)

となります。

 

＜モレラの定理＞～コ－シ－の積分定理の逆

閉曲線C上の連続関数f(z)の積分に関して、∫_C f(z)dz＝0　ならば、f(z)は閉曲線C内で正則である。

証明）z₀からzまでの積分経路をCとします。

　F(z)＝∫_C＝[z_0,z_] f(z)dz

zからz＋Δzまでの経路Lを、

• ξ(t)＝z＋Δz・t　(0≦t≦1)

で定義します。

• dz＝ξ’(t)dt＝Δzdt

が成り立ち、

　F(z＋Δz)＝∫_C+L f(z)dz

と書けます。以下にF(z)の導関数F’(z)が存在し、F’(z)＝f(z)となることを示します。

　　｜[F(z＋Δz)－F(z)]/ Δz－f(z)｜＝｜[∫_C+L f(z)dz－∫_C f(z)dz] /Δz－f(z)｜

　＝｜(1/Δz)∫_[z,z＋Δz] f(z)dz－f(z)｜＝｜(1/Δz)∫_[0,1] f(ξ(t)) Δzdt－f(z)｜

　＝｜∫_[0,1] f(ξ(t)) dt－f(z)｜

　≦∫_[0,1]｜f(ξ(t))－f(z)｜dt ≦∫_[0,1]εdt＝ε

ここでf(ξ)は連続なので、任意のε＞0に対して、｜f(ξ)－f(z)｜＜ε を満たす、｜ξ－z｜＜ΔzなるΔz＞0が存在します。ε→0とΔz→0は対応しています。

　Iim_[Δz→0]｜[F(z＋Δz)－F(z)]/ Δz－f(z)｜≦Iim_[Δz→0]ε(Δz)→0

よって、F(z)の導関数F’(z)が存在し、F’(z)＝f(z)となります。F(z)の導関数が存在するから、F(z)は正則です。グルサの定理より、F’(z)も正則になります。F’(z)＝f(z)なので、f(z)も正則になります。従って、閉曲線Cに対して、∫_C f(z)dz＝0　ならば、f(z)はC内で正則であることが示されました。

 

[Ⅶ] 素数定理　Lim _[x→∞] π(x) logx／x＝1　の証明

（1）Lim_[x→∞]π(x)log(x)/x≧1　を示します。

チェビシェフのシータ関数には

• θ(x)＝Σ_[p≦x] log(p)≦{Σ_[p≦x]1} log(x)＝π(x) logx

なる性質があります。x＞0について、[Ⅵ]より

• π(x) logx／x ≧ θ(x)／x　→1　as　x→∞

よって、Lim_[x→∞]π(x)log(x)/x≧1　となります。

（2）Lim_[x→∞] π(x) log(x)/x≦1　を示します。

任意のε＞0に対して、十分大きいxをとれば、ε・log(x)を大きくとることができるから、

　log(x)－ε・log(x)≦log(p)≦log(x)　→　0＜x^1－ε≦p≦x　

なる素数pが存在します。

θ(x)＝Σ_[p≦x] log(p) ≧ Σ[x^1－ε＜p≦x] log(p) ≧Σ[x^1－ε＜p≦x] log(x^1－ε)

　 ＝(1－ε)log(x)・Σ[x^1－ε＜p≦x]1＝(1－ε)log(x)・(π(x)－π(x^1－ε))

よって、

   θ(x) ≧(1－ε)log(x)・(π(x)－π(x^1－ε))

   θ(x)／x (1－ε) ≧π(x) log(x)/x－π(x^1－ε) log(x)/x

すなわち

  π(x) log(x)/x ≦ 1/(1－ε)・θ(x)/x＋π(x^1－ε) log(x)/x

                     ≦1/(1－ε)・θ(x)/x＋x^1－ε・log(x)/x

となる。ここで

    x^1－ε・log(x)/x＝log(x)/x^ε＝1/ε・log(x^ε)/x^ε

より、任意のε＞0に対して

  π(x) log(x)/x≦1/(1－ε)・θ(x)/x＋1/ε・log(x^ε)/x^ε　→　1/(1－ε)　as x→∞

が成り立つ。極限をとると

    Lim_[x→∞] π(x) log(x)/x≦1

となる。

（3）（1）と（2）から、素数定理

　　Lim_[x→∞] π(x) log(x)/x＝1

が証明されました。

 

[定理A]　Newmanの解析定理

t≧0で有界かつ可積分な関数f(t)に対して、

g(z)＝∫_[0，∞] f(t)exp[－zt] dt　Re(z)＞0

がRe(z)≧0で正則であれば、

　g(0)＝∫_[0，∞] f(t) dt

が存在する。つまり正則関数

　g_T(z)＝∫_[0，T] f(t)exp[－zt] dt

に対して、

lim_[T→∞]g_T(0)＝g(0)

が存在する。

[Ⅵ] θ(x)～x　の証明

　θ(x)～x の定義は、lim_[x→∞] θ(x)/x＝1　です。これは、任意のε＞0、∃x＞0に対して、

　　1－ε＜θ(x)/x＜1＋εと同値です。あるいは

• 任意のλ＞1に対してθ(x)＜λx　かつ
• 任意のλ＜1に対してλx＜θ(x)

と同値です。この命題を否定して、

• λ＞1に対してθ(x)≧λx　かつ
• λ＜1に対してλx≧θ(x)

なるλが存在するとして、矛盾を導きます。

（1）λ＞1に対してθ(x)≧λx　なるλが存在するとして、矛盾を導きます。

　λ＞1のとき、x≦t≦λxなるtに対して、θ(t)≧θ(x)であり

• θ(t)≧θ(x)≧λx　→　(θ(t)－t)／t²≧(λx－t)／t²

　であるから、

• ∫_[x,λx] [(θ(t)－t)／t²] dt ≧∫_[x,λx] [(λx－t)／t²] dt＝∫_[1,λ] [(λ－s)／s²] ds＝δ(λ)＞0

　が成り立ちます。ここでt=xsとおいて、積分変数をtからsに変換しました。

(Ⅴ)より積分

• F(x)＝∫_[1,x] [(θ(t)－t)／t²] dt　→　F（∞）as　x→∞

は収束するので、x→∞で

• 0＜δ(λ)≦∫_[x,λx] [(θ(t)－t)／t²] dt＝F(λx)－F(x)　→　0　as　x→∞

となり、矛盾することが示せました。

（2）λ＜1に対してλx≧θ(x)なるλが存在するとして、矛盾を導きます。

　λ＜1のとき、λx≦t≦xなるtに対して、θ(t)≦θ(x)であり、

• θ(t)≦θ(x)≦λx　→　(θ(t)－t)／t²≦(λx－t)／t²

　であるから、

• ∫_{[λx, x]} [(θ(t)－t)／t²] dt ≦∫_{[λx, x]} [(λx－t)／t²] dt＝∫_[λ,1] [(λ－s)／s²] ds＝δ(λ)＜0

　が成り立ちます。ここでt=xsとおいて、積分変数をtからsに変換しました。

　(Ⅴ)より積分

• F(x)＝∫_[1,x] [(θ(t)－t)／t²] dt　→　F（∞）as　x→∞

　は収束するので、x→∞で

• 0＞δ(λ)≧∫_{[λx, x]} [(θ(t)－t)／t²] dt＝F(x)－F(λx)　→　0　as　x→∞

　となり、矛盾します。よって背理法より、lim_[x→∞] θ(x)/x＝1　が示されました。

[Ⅴ]　∫_[1，∞] [θ(x)－x]／x² dxは収束する。

上記の積分の収束を命題[Ⅲ] 、[Ⅳ]、[定理A]を用いて5段階で証明します。

（1）　Φ(s)＝s∫_[1，∞] θ(x)／x^ｓ+1 dx、Re(s)＞1　が成り立つことを示します。

s∫_[1，∞] θ(x)／x^ｓ+1 dx＝s∫_[1，∞]Σ_[p≦x] log(p)／x^ｓ+1 dx

＝s∫_[1，2]0 dx＋s∫_[2，3] log2／x^ｓ+1dx＋s∫_[3，5](log2＋log3)／x^ｓ+1 dx＋・・・

＝－[log2／x^ｓ]_x=2,3－[(log2+log3)／x^ｓ]_x=3,5－[(log2+log3+log5)／x^ｓ]_x=5,7＋・・・

＝－(log2／3^s－log2／2^s)－[ (log2+log3)／5^s－(log2+log3)／3^s) ]

　－[ (log2+log3+log5)／7^s－(log2+log3+log5)／5^s) ]

　－[ (log2+log3+log5+log7)／11^s－(log2+log3+log5+log7)／7^s) ]－・・・

＝log2／2^s＋log3／3^s＋log5／5^s＋log7／7^s＋・・・

＝Σ_[p]logp／p^s ＝Φ(s)

（2）f(t)＝θ(e^t)e^－t－1　（t≧0）は有界かつ可積分である、ことを示します。

 (Ⅲ)でx＝e^tとして、あるＫ＞0が存在して、｜θ(e^t)｜≦Ｋe^t だから

   ｜f(t)｜＝｜θ(e^t)e^－t－1｜≦｜θ(e^t)｜e^－t＋1＝Ｋe^t e^－t＋1＝Ｋ＋1　

となり、f(t)は有界な関数である。

（3）g(z)＝Φ(z+1)／(z+1)－1/z　　Re(z)＞0　を示します。

x＝e^tとおいて置換積分を実施する。dx＝xdt、t：0→∞、x：1→∞、

e^－zt＝(e^t)^－z＝x^－zに注意すると、

　g(z)＝∫_[0，∞] (θ(e^t)e^－t－1)exp[－zt] dt

　　＝∫_[1，∞] (θ(x)x^－1) x^－z dx/x－[e^－zt／－z]_t=0,∞

　　＝∫_[1，∞] (θ(x)／x^z＋2)dx－1/z

　　＝Φ(z＋1)／(z＋1)－1/z

が示されました。

（4）g(z)はRe(z)≧0で正則である、ことを示します。

(Ⅲ)より、Φ(s)－1/(ｓ－1)はRe(s)≧1で正則なので、s＝z＋1として

　　Re(s)＝Re(z)＋1≧1　→　Re(z)≧0　

Φ(z＋1)－1/zはRe(z)≧0で正則なので、正則関数h(x)を用いて、

　　Φ(z＋1)－1/z＝h(x)　

と表せます。

　g(z)＝Φ(z＋1)／(z＋1)－1/z

　　　＝（h(x)＋1/z）／(z＋1)－1/z＝

　　　＝h(x)／(z＋1)＋1／z(z＋1)－1/z

　　　＝h(x)／(z＋1)＋[1－(z＋1)]／z(z＋1)

　　　＝[h(x)－1]／(z＋1)

　g(z)は、z=－1に極をもちますが、Re(z)≧0で正則であることが示されました。

（5）g(0)＝∫_[0，∞] f(t) dt＝∫_[1，∞] [θ(x)－x]／x² dx　が収束する、ことを示します。

　（2）より関数f(t)＝θ(e^t)e^－t－1はt≧0で有界かつ可積分であり、

　（4）よりg(z)＝∫_[0，∞] f(t)exp[－zt] dt がRe(z)≧0で正則である

従ってNewmanの解析定理により

　　g(0)＝∫_[0，∞] f(t) dt＝∫_[0，∞] (θ(e^t)e^－t－1) dt

が存在します。（3）と同様にx＝e^tとおいて置換積分を実施すると、

　　g(0)＝∫_[1，∞] (θ(x)x^－1－1) dx/x＝∫_[1，∞] [θ(x)－x]／x² dx

が収束することが示されました。

[Ⅳ] θ(x)＝Ｏ(x)　の証明

チェビシェフのシータ関数：θ(x)＝Σ_[p≦x] log(p) がオーダ－xであること、すなわち

・　∃ｋ＞0　｜θ(x)｜≦ｋx          

を3段階で証明します。

（1）2nlog2≧θ(2n)－θ(n)　の証明

2項定理より

2²ⁿ＝(1＋1)²ⁿ＝Σ_{[k＝1～2n] 2n}C_ｋ1^k1^2n-k≧_2nC_n＝2n・(2n－1)・(2n－2)・・(n+2)・(n+1)／n！

_2nC_nは自然数なので、分母のｎ！は約分されて1になります。しかしn+1＜p≦2nの素数pはn！の中には存在しないので、約分されずに分子に残ります。右辺はn+1＜p≦2nの素数pの積Π_{[n+1≦p≦2n]} pより大きくなるので、

・　2²ⁿ≧Π_{[n+1≦p≦2n]} p

が成り立ちます。一方

・　θ(2n)－θ(n)＝Σ_[p≦2n] log(p)－Σ_[p≦n] log(p)＝Σ_{[n+1≦p≦2n]} log(p)

なので、

・　exp[θ(2n)－θ(n)]＝exp[Σ_{[n+1≦p≦2n]} log(p)]＝Π_{[n+1≦p≦2n]} p

です。よって

・　2²ⁿ≧exp[θ(2n)－θ(n)]　→　2n・log2≧θ(2n)－θ(n)

が成り立ちます。

Eg.  ₁₆C₈=16・15・14・13・12・11・10・9／8・7・6・5・4・3・2・1

　　　　＝2・3・13・11 ＞11・13（8+1≦11,13≦16）

（2）2^ｍ+1・log2＞θ(2^m)　の証明

　上式にn＝2^k－1を代入すると、2^k・log2≧θ(2^k)－θ(2^k－1)が成り立つ。

k＝1：　2¹・log2≧θ(2¹)－θ(1)　

k＝2：　2²・log2≧θ(2²)－θ(2¹)

k＝3：　2³・log2≧θ(2³)－θ(2²)

・・・ 　　・・・・

k＝m－1：2^m－1・log2≧θ(2^m－1)－θ(2^m－2)

k＝m：　 2^m・log2≧θ(2^m)－θ(2^m－1)

をすべて加えると、θ(1)＝0より

　　log2・Σ_[k＝1～m]2^k ≧θ(2^m)

を得ます。ここで

　　Σ_[k＝1～m]2^k＝2^m+1－2＜2^m+1

だから、

　　2^m+1 log2＞θ(2^m)

が示されました。

(3) θ(x) ≦4log2・x

x≧1なる整数xに対して、∃m∊N、2^m≦x≦2^m+1

θ(x)は非減少関数なので、（2）より

　　0≦θ(x) ≦θ(2^m+1)＜2^m+2 log2≦4 log2・2^m≦4 log2・x

よって、K＝4 log2とおくと

　　θ(x) ≦Kx、　→　θ(x)＝O(x)

が示されました。

[Ⅲ] 　Φ(s)－1/(ｓ－1)はRe(s)≧1で正則である

という命題を5段階に分けて証明します。これは素数定理の証明で最も本質的な部分の証明です。

（1）ζ’(s)/ζ(s) ＋1/(s－1)　はRe(s)≧1で正則である、を示します。

　　ζ(s)‐1/(s－1)はRe(s)＞0で正則なので、係数a_nを用いて

・    ζ(s)＝1/(s－1)＋Σ_{[n＝0～∞]} a_n (s－1)ⁿ

と表示できます。項別微分ができるので、

・     ζ’(s)＝－1/(s－1)²＋Σ_{[n＝1～∞]} na_n (s－1)^n－1

となります。よって

　　　(s－1)ζ’(s)/ζ(s)

　　＝(s－1) [－1/(s－1)²＋Σ_{[n＝1～∞]} na_n (s－1)^n－1]／[1/(s－1)＋Σ_{[n＝0～∞]} a_n (s－1)ⁿ]

　　＝[－1＋Σ_{[n＝1～∞]} na_n (s－1)ⁿ⁺¹]／[1＋Σ_{[n＝0～∞]} a_n (s－1)ⁿ⁺¹]

　　→－1　as　s→1

つまり

• ζ’(s)/ζ(s) ＋1/(s－1)　はRe(s)≧1で正則である。

ことが示されました。

（2）Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)＋1/(s‐1)]－Σ[p] log(p)／p^s(p^s‐1) 　を示す。

ゼータ関数ζ(s)のオイラ－積表示

• ζ(s)＝Π[p] [1/(1‐1/p^s)]

の対数を取ると、

• log[ζ(s)]＝‐Σ[p] log(1‐1/p^s)

となります。これを微分した導関数は

• (1/p^s)′＝exp(‐slog(p))′＝‐log(p)／p^s

となります。よって

• ζ′(s)／ζ(s)＝‐Σ[p] (1‐1/p^s)′／(1‐1/p^s)＝‐Σ[p] log(p)/p^s／(1‐1/p^s)

より

• ζ′(s)／ζ(s)＝‐Σ[p] log(p)／(p^s‐1)

となります。ここでさらに

• 1/(p^s‐1)＝1/p^s＋1/ p^s(p^s‐1)

を用いると、

• ζ′(s)／ζ(s)＝‐Σ[p] log(p)／p^s－Σ[p] log(p)／p^s(p^s‐1)

つまり、ゼータ関数ζ(s)とファイ関数Φ(s)の関係式

• ζ′(s)／ζ(s)＝‐Φ(s)－Σ[p] log(p)／p^s(p^s‐1)　

が得られます。変形すると

• Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)＋1/(s‐1)]－Σ[p] log(p)／p^s(p^s‐1) 　

なる表式が得られました。

（3）右辺2項目Σ[p] log(p)／p^s(p^s‐1)はRe(s)＞1/2で正則である、を示します。

Re(s)＞1/2のとき

　｜p^s｜＞｜2^s｜＝2^Re(s) ＞√2

である。このとき

　　｜p^s｜＜(2＋√2)(｜p^s｜－1)　 →　1/(｜p^s｜－1)＜(2＋√2) /｜p^s｜

が成り立つ。理由は

　　　(2＋√2)＜ (1＋√2)｜p^s｜　→　√2＜｜p^s｜

　　　(2＋√2)/ (1＋√2)＝(2＋√2) (√2－1)＝2√2－2＋2－√2＝√2

従って

　　｜log(p)／p^s(p^s‐1)｜＜ log(p)／(｜p^s｜｜p^s‐1｜)＜ (2＋√2)・log(p)／p^2Re(s)

素数に関する和をとると
　　Σ[p]｜log(p)／p^s(p^s‐1)｜＜(2＋√2)・Σ[p] log(p)／p^2Re(s)＝(2＋√2)・Φ(2Re(s))

Φ(2Re(s))は2Re(s)＞1で収束するので、ワイヤストラスの収束判定定理よりRe(s)＞1/2の

領域で、Σ[p] log(p)／p^s(p^s‐1)は広義一様収束し、正則関数になることが示されました。

（4）Re(s)＝1でζ(s)＝0なる零点が存在しない、ことを示す。

複素共役変換：Conj(a+bi)＝a－bi、に関して

　　Conj[ζ(s)]＝ζ(Conj(s))

が成り立つ（鏡像原理）。なぜなら、

　　Conj[ζ(s)]＝Σ1/n^{Re(s)－Im(s)} ＝Σ1/n^Conj[s] ＝ζ(Conj(s))

だからです。実数a＞0に対して、

　　ζ(1＋ai)＝0　ならば　ζ(1－ai)＝0

　　ζ(1＋2ai)＝0　ならば　ζ(1－2ai)＝0

が成り立つ。

今、s＝1＋ai がζ(s)のu位の零点、s＝1＋2ai がζ(s)のv位の零点だとすると、

u≧0、v≧0なる整数を用いて

　ζ(s)＝b_u(s－1－ai)^u＋b_u+1(s－1－ai)^u+1＋b_u+2(s－1－ai)^u+2＋・・・

　ζ(s)＝C_v(s－1－2ai)^v＋C_v+1(s－1－2ai)^v+1＋C_v+2(s－1－2ai)^v+2＋・・・

と展開できます。鏡像原理から同様に、s＝1－ai がζ(s)のu位の零点、s＝1－2ai がζ(s)の

v位の零点となるので、

　ζ(s)＝b_u(s－1＋ai)^u＋b_u+1(s－1＋ai)^u+1＋b_u+2(s－1＋ai)^u+2＋・・・

　ζ(s)＝C_v(s－1＋2ai)^v＋C_v+1(s－1＋2ai)^v+1＋C_v+2(s－1＋2ai)^v+2＋・・・

と展開することもできます。各収束円内で項別微分して、

　ζ′(s)＝－1/(s－1)²＋a₁＋2a₂(s－1)＋3a₃(s－1)²＋・・・

　ζ’(s)＝ub_u(s－1∓ai)^u－1＋(u+1)b_u+1(s－1∓ai)^u＋(u+2)b_u+2(s－1∓ai)^u+1＋・・・

　ζ’(s)＝vC_v(s－1∓2ai)^v－1＋(v+1)C_v+1(s－1∓2ai)^v＋(v+2)C_v+2(s－1∓2ai)^v+1＋・・・

Φ関数に関して、

• 　Φ(s)＝－ζ′(s)／ζ(s)－Σ[p] log(p)／p^s(p^s‐1)　

が成り立っていました。このとき1）～3）の性質があります。

1) lim_[ε→0] εΦ(1+ε)＝1　e.　Φ(s)～1/(s－1)の項がある場合

　εΦ(1+ε)＝－εζ′(1+ε)／ζ(1+ε)－εΣ[p] log(p)／p^1+ε(p^1+ε‐1)　

　　＝－ε[－1/ε²＋a₁＋2a₂ε＋3a₃ε²＋・・・]/ [1/ε＋a₀＋a₁ε＋a₂ε²＋・・・]－O(ε)

　　＝[1－a₁ε²＋2a₂ε³＋3a₃ε⁴＋・・]/ [1＋a₀ε＋a₁ε²＋a₂ε²＋・・]－O(ε)

　　→1  as ε→0

2) lim_[ε→0] εΦ(1+ε±ai)＝－u　e.　Φ(s)～－u/(s－1∓ai)の項がある場合

　εΦ(1+ε±ai)＝－εζ′(1+ε±ai)／ζ(1+ε±ai)－εΣ[p] log(p)／p^1+ε±ai (p^1+ε±ai‐1)　

＝－ε[ub_uε^u－1＋(u+1)b_u+1ε^u＋(u+2)b_u+2ε^u+1＋・]/ [b_uε^u＋b_u+1ε^u+1＋b_u+2ε^u+2＋・] －O(ε)

＝－[ub_u＋(u+1)b_u+1ε＋(u+2)b_u+2ε²＋・・]/ [b_u＋b_u+1ε¹＋b_u+2ε²＋・・]－O(ε)

 →－u　as ε→0

3) lim_[ε→0] εΦ(1+ε±2ai)＝－v　e.　Φ(s)～－v/(s－1±2ai)の項がある場合

　εΦ(1+ε±2ai)＝－εζ′(1+ε±2ai)／ζ(1+ε±2ai)－εΣ[p] log(p)／p^1+ε±2ai (p^1+ε±2ai‐1)　

＝－ε[vC_vε^v－1＋(v+1)C_v+1ε^v＋(v+2)C_v+2ε^v+1＋・]/ [C_vε^v＋C_v+1ε^v+1＋C_v+2ε^v+2＋・]－O(ε)

＝－[vC_v＋(v+1)C_v+1ε＋(v+2)C_v+2ε²＋・・]/ [C_v＋C_v+1ε¹＋C_v+2ε²＋・・]－O(ε)

→－v　as ε→0

4）恒等式：

• [2Re(p^ia/2)]⁴＝p^2ia＋4p^ia＋6＋4p^－ia＋p^－2ia

が成り立つ。

[2Re(p^ia/2)]⁴＝[p^ia/2＋p^－ia/2]⁴＝[p^ia＋p^－ia＋2]²＝p^2ia＋p^－2ia＋4＋2 p^iap^－ia＋4 p^ia＋4 p^－ia

　               ＝p^2ia＋4p^ia＋6＋4p^－ia＋p^－2ia

5）εΣ_[p]log(p)/p^1+ε[2Re(p^ia/2)]⁴

　　＝εΦ(1＋ε－2ai)＋4εΦ(1＋ε－ai)＋6εΦ(1＋ε)＋4εΦ(1＋ε＋ai)＋εΦ(1＋ε＋2ai)

　　→　2(3－4u－v)　as ε→0

が成り立つ。

　　0＜εΣ_[p]log(p)/p^1+ε[2Re(p^ia/2)]⁴

　　　＝εΣ_[p]log(p)/p^1+ε[p^2ia＋4p^ia＋6＋4p^－ia＋p^－2ia]

　　　＝εΣ_[p]log(p)/p^1+ε－2ia＋4εΣ_[p]log(p)/p^1+ε+ia＋6εΣ_[p]log(p)/p^1+ε

　　　　　　　　　　　　　＋4εΣ_[p]log(p)/p^1+ε－ia＋εΣ_[p]log(p)/p^1+ε+2ia

　　　＝εΦ(1＋ε－2ai)＋4εΦ(1＋ε－ai)＋6εΦ(1＋ε)＋4εΦ(1＋ε＋ai)＋εΦ(1＋ε＋2ai)

　　　→　－v－4u＋6－4u－v ＝ 2(3－4u－v)＞0　as ε→0

6）ζ(s)はs＝1±aiに零点を持たない、を示す。

結局

• u≧0、v≧0、3－4u－v＞0　

より、u＝0　が結論される。任意の正数aに対して、ζ(s)はs＝1±aiに零点を持たない。

• ζ(s)＝b₀＋b₁(s－1±ai)＋b₂(s－1±ai)²＋・・・、b₀≠0

と展開できる。以上をまとめると

（1）ζ’(s)/ζ(s) ＋1/(s－1)　はRe(s)≧1で正則である。　

（2）Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)＋1/(s‐1)]－Σ[p] log(p)／p^s(p^s‐1)

（3）Σ[p] log(p)／p^s(p^s‐1)はRe(s)＞1/2で正則である。

（4）Re(s)＝1でζ(s)＝0なる零点が存在しない。

以上より、

• Φ(s)‐1/(s‐1)はRe(s)≧1で正則である。

と結論できます。

＜メモ＞

・Re(s)＞1で、オイラ－積　ζ(s)＝Π[p] [1/(1‐1/p^s)]が収束する

ことを示しておきましょう。

• 1/(1‐1/p^s)＝＝p^s/(p^s‐1)＝1＋1/(p^s‐1)

と書けます。今

｜p^s｜＝p^Re(s) ＞p≧2　より、　2｜p^s｜－｜p^s｜＞2　→　2(｜p^s｜－1)＞｜p^s｜＞0　

→　1/(｜p^s｜－1)＜2/｜p^s｜

が成り立ちます。

• ｜1/(p^s‐1)｜≦1/(｜p^s｜‐1)＜2/｜p^s｜＝2/p^Re(s)

が成り立ちます。素数pに対してn≦p＜n+1なる自然数nが存在します。

• f_n(s)＝δ_np/(p^s‐1)、M_n＝1/n^Re(s)

とすると、上の性質より

• ｜f_n(s)｜≦｜1/(p^s‐1)｜≦ 1/(｜p^s｜‐1)≦ 2/p^Re(s)≦ 2/n^Re(s)＝ M_n

であり、Re(s)＞1で

• Σ_{[n＝1～∞]} M_n＝ 2Σ_{[n＝1～∞]} 1/n^Re(s) ＝2ζ( Re(s))　が収束する。

従って、無限積の収束判定の定理より、オイラ－積

• Π_[n] [1＋f_n(s)]＝ Π_[n] [1＋δ_np/(p^s‐1)] ＝ Π_[p] [1＋1/(p^s‐1)]＝ Π_[p] [1/(1‐1/p^s)]

が収束します。

＜無限積の収束判定定理＞

関数列{f_n(s)}_{n＝1.2.3・・}に対して、正の数列{M_n} _{n＝1.2.3・・}が、任意のｓの領域において

1）｜f_n(s)｜≦M_n

2）Σ_{[n＝1～∞]} M_n＜∞

の2条件を満たすならば、無限積

• Π_{[n＝1～∞]} [1＋f_n(s)]

が収束する。

証明）　S_n＝Σ_[k=1～n] f_k(s)、P_n＝Π_[k＝1～n] [1＋f_k(s)]とする。

S_n＝Σ_[n=1～n] f_n(s)＜P_n＝Π_[k＝1～n] [1＋f_k(s)]＜Π_[k＝1～n]＝exp[Σ_[k＝1～n]f_k(s)]＝exp[S_n]

0＜｜S_n｜≦Σ_[n=1～n] M_n＜｜P_n｜＜exp[｜S_n｜] ≦exp[Σ_[n=1～n] M_n]

この関係は、n→∞では、

0＜｜S_∞｜≦Σ_[n=1～∞] M_n＜｜P_n＝∞｜＜exp[Σ_[n=1～∞] M_n]＜∞

となるので、Σ_[n=1～∞] M_nが収束するならば、｜P_n＝∞｜＝Π_{[n＝1～∞]} [1＋f_n(s)]が存在する。

注意：｜P_n＝∞｜が存在すれば、｜S_n＝∞｜も存在します。

リ－マンのゼータ関数ζ(s)は、

• ζ(s)＝Σ_{[n＝1～∞]} 1／n^s＝1＋1／2^s＋1／3^s＋・・・

Re(s)＞1で収束します。これをζ(s)のディリクレ級数表示ともいいます。

ｓ＞1ならば、2≦n≦Nに対して、n－1＜x＜nの時、

• 　1/n^s＜1/x^s＜1/(n－1)^s

が成り立つので、

• 1/n^s＜∫_[n－1,n]1/x^s dx ＜1/(n－1)^s
• Σ_[n=2～N] 1/n^s＜Σ_[n=2～N]∫_[n－1,n]1/x^s dx ＜Σ_[n=2～N] 1/(n－1)^s
• Σ_[n=2～N] 1/n^s＜∫_[1,N]1/x^s dx ＜Σ_[n=2～N] 1/(n－1)^s
• Σ_[n=1～N] 1/n^s－1＜∫_[1,N]1/x^s dx ＜Σ_{[n=1～N－1]} 1/n^s

ここで

• ∫_[1,N]1/x^s dx＝[x^1－S/(1－s)]x＝1,N　＝1/(s‐1)[1－N^1－s]＜1/(s‐1)

なので、

• Σ_[n=1～N] 1/n^s＜1＋1/(s‐1)　→　Σ_[n=1～∞] 1/n^sは収束する

従って

• 1/(s‐1) ≦ζ(s) ≦1＋1/(s‐1)　for s＞1

より、

• Lim_[s→+1] ζ(s)＝∞　かつ　Lim_[s→+1] (s‐1)ζ(s)＝1

が得られます。

 

s＝1のときは、ζ(s)は調和級数となり

• Σ_{[n＝1～∞]} 1／n＝1＋1／2＋1／3＋・・・＝log(∞)

対数発散をします。これは積分判定法から分かります。

積分判定法とは、正の単調減少関数f(x)によって、数列a_nを、a_n＝f(n)と定義すると、

• Σ_[n=1～∞] a_nが収束　⇔　∫_[1,∞] f(x) dxが収束

が成り立つというものです。よって

• ∫_[1,∞] 1/x dx＝log(∞)　→　Σ_{[n＝1～∞]} 1／n＝log(∞)

だと分かります。あるいは任意の正の整数ｋに対して

• Σ_[n=1～2k]1/n ＞ 1＋k/2　→　as k →∞

により示すことができます。

 

ゼータ関数ζ(s)のオイラ－積表示は

• ζ(s)＝Π_[p] [1/(1‐1/p^s)]

はディリクレ級数表示と一致するでしょうか。

s＞1のとき、有限積

• P_N(s)＝Π_[p≦N] [1/(1‐1/p^s)]

を考えます。

• 1/(1‐1/p^s)＝Σ_[k=0～∞] (p^－s)^k＝1＋1/p^s＋1/p^2s＋1/p^3s＋・・・

を代入して、P_N(s)を展開すると、素因数分解の一意性より

• Σ_[n＝1～N] 1/n^s ＜ P_N(s)＝Σ[nの各素因数≦N] 1/n^s ＜Σ_{[n＝1～∞]} 1/n^s＝ζ(s)

が成り立つので、

• Π_[p] [1/(1‐1/p^s)]＝Lim_[N→∞] P_N(s)＝ζ(s)

ゼータ関数ζ(s)はオイラ－積表示可能であることが示されました。

 

ゼータ関数ζ(s)は、s＞0（s≠1）に拡張することができます。

• ζ(s)＝L(s)／(1－2^1－s)　、L(s)＝Σ_{[n＝1～∞]}(－1)^(n－1)/n^s

右辺はs＞0（s≠1）で収束します。実際部分和L_N(s)＝Σ_[n＝1～N](－1)^(n－1)/n^sを考えると、

• 0＜1－1/2^s＝L₂＜L₄＜・・・＜L_2N＜L_2N+2＜L_2N+1＜L_2N－1＜・・・＜L₃＜L₁＝1

偶数番目の部分和L_2nは上に有界で単調増加、奇数番目の部分和L_2n-1は下に有界で単調減少なので、それぞれ収束し、s＞0のとき

• L_2N－L_2N-1＝－1/(2N)^s　→ 0 　as 　N →∞

だから、

• Lim_[N→∞] L_2N＝Lim_[N→∞]L_2N-1＝L(s)

となります。

• ζ(s)‐L(s)＝2Σ_{[n＝1～∞]}1/(2n)^s＝2^(1－s)・Σ_{[n＝1～∞]}1/n^s＝2^(1－s) ζ(s)

よって、

• ζ(s)＝L(s)／(1－2^1－s)　for　s＞0（s≠1）

が示されました。s＞0のときは、ζ(s)はL(s)/(1－2^1－s)だと再定義します。

0＜s＜1のとき、L(s)＞0で(1－2^1－s)＜0なので、ζ(s)＜0であり、

• Lim_[s→1-δ] ζ(s)＝－∞

となります。正の関数を解析接続すると負の関数になるのは驚きです。

実はガンマ関数を用いると、s＜0の領域にもζ(s)を拡張することができます。

結果だけ書くと、

• ζ(s)＝2^sπ^s‐1・sin(πs/2)・Γ(1－s)・ζ(1－s)　 s＜0（s≠1）

右辺は1－s＞1で定義されるので、左辺はｓ＜0で定義できます。

• sin(πs/2)＝0　for　s＝－2、－4、－6、・・・

なので、

• ζ(－2k)＝0　（kは正の自然数）

となります。これらの負の零点をゼータ関数の自明な零点といいます。

下図にゼータ関数の外形を示します。N＝10000までの和で計算表示しました。本来、赤線と青線はｓ＝0でｙ＝－1/2で接続します。ｓ＜0の部分は、振動しており、負の偶数は零点になっています。

 

実数x以下の素数の個数π(x)は

• π(x)＝Σ_[p≦x] 1

と表せます。π(x)は「素数ｐ（＝2、3，・・・Ｐ≦x）がx以下の最大の素数Pになるまで1を加え続ければ得られます。π(x)は素数を段差とする階段関数になっています。素数定理は

• π(x)～x／logx

すなわち

• Lim _[x→∞] π(x) logx／x＝1

が成り立つというものです。

まずチェビシェフのシータ関数

• θ(x)＝Σ_[p≦x] log(p)

を考えます。この関数には

• θ(x)≦π(x) logx

なる性質があります。実際

• θ(x)＝Σ_[p≦x] log(p)≦{Σ_[p≦x]1} log(x)＝π(x) logx

によって確かめられます。

• π(x) logx／x ≧ θ(x)／x　→1　as　x→∞

ですから、素数定理を示すのに、

• Lim _[x→∞] θ(x)／x＝1

すなわち

• θ(x)～x

が成り立つことを示す必要があります。これは任意のλに対して

• ∀ λ＞1 θ(x)≦λx　かつ　∀ λ＜1　θ(x)≦λx

が成り立つことと同値です。この命題を否定して、

• θ(x)≧λx　for　λ＞1　あるいは　θ(x)≦λx　for　λ＜1

なるλが存在するとして、矛盾を導きます。　x≦t≦λxなるtに対して

• θ(t)≧θ(x)≧λx　→　(θ(t)－t)／t²≧(λx－t)／t²

であるから、

• ∫_[x,λx] [(θ(t)－t)／t²] dt ≧∫_[x,λx] [(λx－t)／t²] dt＝∫_[1,λ] [(λ－s)／s²] ds＝δ(λ)＞0

が成り立ちます。ここでt=sxとおいて、積分変数をtからsに変換しました。積分

• F(x)＝∫_[1,x] [(θ(t)－t)／t²] dt　→　F（∞）as　x→∞

が収束すれば、左辺の極限値がゼロ

• 左辺＝F(λx)－F(x)　→　0　as　x→∞

になり、左辺≧δ(λ)＞0に矛盾することが示せます。

先ほどの積分は、x＝exp(t) と置いて、xからtに変数変換すると、dx＝xdt

• F(∞)＝∫_[1,∞] [(θ(x)－x)／x²] dx＝∫_[0,∞] (θ(e^t) e‐^t－1) dt＝∫_[0,∞] f(t) dt
• f(t)＝θ(e^t) e‐^t－1

と書けます。ここで、f(t)のラプラス変換

• g(z)＝∫_[0,∞] f(t) e^－zt dt

を考えます。Newman教授は、f(t)が有界で、複素関数g(z)がRe(z)≧0で正則ならば、

• g(0)＝∫_[0,∞] f(t) dt

が存在するという解析定理を発見しました。

注意すべきことは、一般に

• Lim_[z→0] ∫_[0,∞] f(t) e^－zt dt = ∫_[0,∞] f(t) dt

が成立しないことです。例えばf(t)＝sin(t)のとき

• g(z)＝∫_[0,∞] sin(t) e^－zt dt＝1/(z²＋1) → 1　as　z→0

となります。しかしg(0)＝∫_[0,∞] sin(t) dtは存在しません。計算を示します。

• g(z)＝∫_[0,∞] 1/2i・(e^it‐e^－it) e^－zt dt=1/2i・[e^it－zt/(i－z)+e^－it－zt/(i＋z)]t=0,∞

＝－1/2i・[1/(i－z)＋1/(i＋z)]＝1/(z²＋1)

実際シ－タ関数は、ある正数Kに対して

• θ(x)≦Kx　e.　 θ(x)＝O(x)：オーダ－ｘ

なる性質があるので、

• ｜f(t)｜＝｜θ(e^t) e‐^t－1｜≦θ(e^t)／e^t＋1≦K＋1

となり、f(t)が有界になります。

複素関数g(z)は、x=exp(t)と変数変換すると、dx=xdt、e^－zt＝1/x^z

• g(z)＝∫_[0,∞] (θ(e^t) e‐^t－1) e^－zt dt＝∫_[1,∞] (θ(x)／x^z+2) dx‐1/z

となります。θ(x)を代入して計算すると

• g(z－1)＝∫_[1,∞] (Σ[p≦x] log(p)／x^z+1) dx‐1/z＝Φ(z)/z‐1/z

なる関係が得られます。

• z∫_[1,∞] (θ(x)／x^z+1) dx＝z∫_[2,3] log2／x^z+1 dx＋z∫_[3,5] (log2+ log3)／x^z+1 dx＋・・・

＝－[log2/x^z]x=2,3－[(log2+log3)/x^z]x=3,5－[(log2+log3+log5)/x^z]x=5,7＋・・・

＝(－log2/3^z+ log2/2^z)－[－(log2+log3)/5^z－(log2+log3)/3^z)]

－[－(log2+log3+ log5)/7^z－(log2+log3+ log5)/5^z)]＋・・・

　　＝log2/2^z＋log3/3^z)＋log5/5^z＋log7/7^z＋・・・

＝Σ_[p] log(p)／p^z＝Φ(z)

関数Φ(s)は

• Φ(s)＝Σ_[p] log(p)／p^s

ここでΣ_[p]は全ての素数の和を取ります。結局

• g(z)＝Φ(z+1)／(z+1)－1/z＝[{Φ(z+1)－1/z}－1]／(z+1)

Newmanの解析定理を適用するには、g(z)がRe(z)≧0で正則でなければなりません。

よって

• Φ(s)－1/(s‐1)がRe(s)≧1で正則である

ことが言えれば良いことが分かります。

ここでリ－マンのゼータ関数ζ(s)

• ζ(s)＝Σ_{[n＝1～∞]} 1／n^s＝1＋1／2^s＋1／3^s＋・・・

を考えます。この関数はRe(s)＞1で収束します。s＝1のときは、ζ(s)は調和級数となり

• Σ_{[n＝1～∞]} 1／n＝1＋1／2＋1／3＋・・・＝log(∞)

対数発散をします。自然数の素因数分解の一意性によって、ゼータ関数ζ(s)は

• ζ(s)＝Π_[p] [1/(1‐1/p^s)]

とも書けます。これをオイラ－積表示といいます。実際

• ζ(s)＝ [1/(1‐1/2^s)]・[1/(1‐1/3^s)]・[1/(1‐1/5^s)]・[1/(1‐1/7^s)]・[1/(1‐1/11^s)]・・・

　　　 ＝[1＋1/2^s＋1/2^2s＋1/2^3s＋1/2^4s＋1/2^5s＋・・・]

・[1＋1/3^s＋1/3^2s＋1/3^3s＋1/3^4s＋1/3^5s＋・・・]

・[1＋1/5^s＋1/5^2s＋1/5^3s＋1/5^4s＋1/5^5s＋・・・]

・[1＋1/7^s＋1/7^2s＋1/7^3s＋175^4s＋1/7^5s＋・・・]・・・

      　＝1＋1／2^s＋1／3^s＋1／2^2s＋1／5^s＋1／2^s3^s＋1／7^s＋1／2^3s＋1／3^2s＋1／2^s 5^s

＋1／11^s＋1／2^2s3^s＋1／13^s＋1／2^s7^s＋1／3^s 5^s＋1／2^4s＋・・・

　　　　＝1＋1／2^s＋1／3^s＋1／4^s＋1／5^s＋1／6^s＋1／7^s＋1／8^s＋1／9^s＋1／10^s

＋1／11^s＋1／12^s＋1／13^s＋1／14^s＋1／15^s＋1／16^s＋・・・

となり、成立しています。ζ(s)のオイラ－積表示の対数を取ると、

• log[ζ(s)]＝‐Σ_[p] log(1‐1/p^s)

となります。これを微分した導関数は

• (1/p^s)′＝exp(‐slog(p))′＝‐log(p)／p^s

となります。よって

• ζ′(s)／ζ(s)＝‐Σ_[p] (1‐1/p^s)′／(1‐1/p^s)＝‐Σ_[p] log(p)/p^s／(1‐1/p^s)

より

• ζ′(s)／ζ(s)＝‐Σ_[p] log(p)／(p^s‐1)

となります。ここで

• 1/(p^s‐1)＝1/p^s＋1/ p^s(p^s‐1)

を用いると、

• ζ′(s)／ζ(s)＝‐Σ_[p] log(p)／p^s－Σ_[p] log(p)／p^s(p^s‐1)

つまり、ゼータ関数ζ(s)とファイ関数Φ(s)の関係式

• ζ′(s)／ζ(s)＝‐Φ(s)－Σ_[p] log(p)／p^s(p^s‐1)　

が得られます。変形すると

• Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)‐1/(1－s)]－Σ_[p] log(p)／p^s(p^s‐1) 　　・・・（＃）

なる表式が得られます。実は右辺2項目はRe(s)＞1/2で正則です。

Φ(s)－1/(s‐1)がRe(s)≧1で正則であることを示すためには、

• ζ′(s)／ζ(s)‐1/(1－s)がRe(s)≧1で正則である

ことを示す必要があります。そのためには

• ζ(s)がRe(s)＝1で零点を持たない。
• ζ(s)‐1/(s‐1)はRe(s)＞0で正則である。

ことを示す必要があります。なぜならそれが成り立てば、ζ(s)はRe(s)＞0でs＝1に極を持つ有理型関数なので、

• Lim_[s→1] (1－s) ζ′(s)／ζ(s)＝1　 for　Re(s)＞1

となるからです。いま

• 1/(s‐1)＝Σ_[n=1～∞] ∫_[n,n+1]1/x^sdx

と書けるので

• ζ(s)‐1/(s‐1)＝Σ_[n=1～∞][1/n^s‐∫_[n,n+1]1/x^sdx]＝Σ_[n=1～∞]∫_[n,n+1][1/n^s‐1/x^s]dx
• ｜∫_[n,n+1][1/n^s‐1/x^s]dx｜≦｜s｜/n^Re(s)+1
• ｜ζ(s)‐1/(s‐1)｜≦Σ_[n=1～∞]｜s｜/n^Re(s)+1＝｜s｜ζ(Re(s)+1)

となります。ζ(Re(s)+1)はRe(s)+1＞1で正則なので、ζ(s)‐1/(s‐1)はRe(s)＞0で正則関数に拡張できます。つまり素数定理の核心はζ(s)がRe(s)＝1で零点を持たないことの証明になります。

 

ゼータ関数ζ(s)のオイラ－積表示

• ζ(s)＝Π_[p] [1/(1‐1/p^s)]

は興味深い関係式です。もしゼータ関数の零点ρが分かれば、

• ζ(s)＝f(s)・Π_[ρ] [s－ρ]

と因数分解できることになります。対数表示をとると

log f(s)＋Σ_[ρ]log (s‐ρ)＝－Σ_[p] log (1‐1/p^s)

が得られます。これはゼータ関数の零点ρに関する和が、全ての素数pに関する和と関係があることを示唆しています。ゼータ関数の零点には、素数の情報が含まれていると考えられます。ゼータ関数はs=－2k＝－2、－4、－6、・・・に自明な零点を持つことが知られています。ζ(0)＝－1/2で、s=0は零点ではありません。

• ゼータ関数の非自明な零点は、Re(1/2)上に存在している

というのが、有名なリーマン予想です。10兆個の零点を調べたところ、全てRe(1/2)上に存在しているようです。しかしその事実を持って、リーマン予想が正しいと結論することはできません。フラクタル曲線で有名なコッホは1901年に、リーマン予想が正しければ、素数の計数関数は

• π(x)～Li(x)＋O(√ｘ・log(x))

と書けると主張しています。リーマン予想は素数分布の予測の精緻化にも役立ちます。

リーマン予想は数論の様々な問題と関連しており、今でも高い関心が注がれています。

＜素数定理＞

自然数x以下の素数の個数をπ(x)とすると、π(x)～x／logxと表される。すなわち

• Lim _[x→∞] π(x) logx／x＝1

が成り立つ（1896年）。

素数定理は1896年にジャック・アダマ－ルとバレ・プ－サンによって独立に証明されました。素数定理は簡潔で分かりやすい定理ですが、証明は難解です。1949年にアトル・セルバ－グやポール・エルディッシュが初等的手法で証明しました。初等的といっても、証明法は技巧的で難いものです。

1980年にドナルド・ニュ－マンが複素関数論を用いて簡潔な素数定理の証明方法を見つけました。1997年に素数定理100周年記念として、ドン・ザギエが5つのステップと解析的定理を用いるニュ－マンの証明法を紹介しました。ここではニュ－マンとザギエによる素数定理の証明を紹介します。複素関数論の威力が良く分かります。

ザギエ教授の経歴

ザギエは西ドイツのハイデルベルクに生まれた。母親は精神科医で、父親はスイスのアメリカン・カリッジの教頭だった。父親が5つの異なる市民権を有していたため、ザギエは若いころ多くの国々で過ごしていた。13歳の時に高校を卒業し、1年間ウィンチェスター・カレッジにて学んだ後、ザギエはMITで3年間学び、学士号と修士号を得、1967年16歳の時プットナム・フェローに指名された。ザギエはボン大学でフリードリッヒ・ヒルツェブルフの下で特性類に関する博士論文を書き、20歳の時に博士号を受けた。23歳の時に教授資格を受け、24歳の時に教授に指名された。

[1] Donald J. Newman, (1980). “Simple analytic proof of the prime number theorem”. American Mathematical Monthly. 87 (9): 693–696.

[2] Don Zagier, (1997). “Newman’s Short Proof of the Prime Number Theorem”. Amer. Math. Monthly 104 (8): 705–708. ショーヴネ賞 (2000)

 

現代情報社会に欠かせなくなった暗号には素数の性質が使われています。素数は1と自分自身以外で割り切れない数のことです。具体的には

• 素数＝{2，3、5、7、11，13，17、19、23、・・・}

なる自然数です。素数には1を含めません。そうすると全ての数は素数の積として一意に表すことができます。いわば素数は自然界の原子のような存在です。しかし素数は無限にあります。

自然数n以下の素数の個数をπ(n)と表します。図1にｙ＝π(x)のグラフを示します。例えば50番目の素数229と95番目の素数499はそれぞれ（229，50）と（499，95）にプロットされています。500以下には95個の素数があるので、π(500)＝95です。

驚くべきことに、素数の出現の仕方には規則性がないのに、素数はほぼ一つの曲線の近傍に分布しているように見えますが、その理由は今でも良く分かっていません。お子さんに素数の分布曲線を見せることで、未知の法則に対する興味関心を引き出すことができるでしょう。

素数を見出す確率はどのくらいでしょうか。1792年にドイツの数学者ガウス（当時15歳）は、数ｎの近傍で素数を見出す確率は1／log(n)と予想しました。その場合に自然数n以下の素数の個数は

• Li(n)＝∫_[2→n] 1/log(t) dt

と表せます。ここでlogは自然対数です。展開近似すると

• Li(n)≒n/log(n)+n／(log(n))＾2　→　n/log(n)　as ｎ→∞

となります。ｎ→∞の極限で両者が一致するという意味で

• Li(n)～n/log(n)

と書き表します。実際に

• π(n)～Li(n)

となっています。ｘが大きい数のとき、ｘまでの数の中に素数を見出す確率π(x)／xは、1／log(x)、すなわち

• π(x)～f(x)＝x／log(x)

と考えられます。図2に10万までの素数の分布曲線を示します。10万程度ではx/log(x)の近似は誤差が大きいことが分かります。

この定理を使うと、例えば100億までに約4.5億個の素数があることがすぐに計算できます。

x＝10ⁿのとき、

• f(10ⁿ)＝10ⁿ／log(10ⁿ)＝log(e)／n・ 10ⁿ≒log（27/10）／n・ 10ⁿ

　　　　＝(3log3－1) ／n・ 10ⁿ≒(0.434／n)×10ⁿ

x＝100億=10¹⁰の時、素数の数は

• f(10¹⁰)≒434／10・ 10¹⁰＝4.34億個

と予想されます。実際、100億より小さい素数の数は

• π(10¹⁰ )­＝455,052,511＝4.55億個

なので、4.6％の誤差で当たっています。Li(x)の場合、

• Li(10¹⁰) ≒ 455,055,615

なので、0.0007%の誤差しかありません。

1749年にオイラ－は

• Z＝1＋1＋1＋1＋1＋・・・＝－1/2

という不思議な級数の値を求めました。時々皆さんも目にすることがあると思います。今日はこの式の意味する所を考えてみます。

まず関数

• f₀(x)＝1/(1＋x)、f₀(1)＝1/2

を考えます。この関数を展開すると

• f(x)＝1－x＋x²－x³＋x⁴－x⁵＋・・・　for　｜x｜＜1

と表すことができます。但しこの関数はｘ＝1では定義されていません。

形式的にｘ＝1を代入し、その値をYとします。

• f(1)＝1－1＋1－1＋1－1＋・・・＝Y

となります。元の関数をｘのｎ次までの展開した関数を

　　f_n(x)=Σ_ｋ＝0～n (－x)^k→　1/(1＋x)　x≠1　as  n→∞

と定義します。グラフにｎ＝10，20、100、1000の場合の関数形を表示します。

nが無限大の極限で、関数f_n(x)はｘ＜1で関数1/(1＋x)に一致することが分かります。つまりｘ→1の片側極限で

• lim x→1 f(x)＝1/2

が成り立っています。そこで

• f(1)＝1/2

と定義すれば、関数f(x)は0≦ｘ≦1で1/(1+x)に一致します。これは

• 　Y＝1－1＋1－1＋1－1＋・・・＝1/2

を示しています。ZもYと同じような意味で値を持つと考えます。そうすると

　2Z＝   2＋   2＋   2＋　 2＋・・・

　 Z＝1＋1＋1＋1＋1＋1＋1＋1＋・・・

を辺々引くと

　Z＝2Z－Z＝－1＋1－1＋1－1＋1－1＋・・・

が得られます。両辺に1を加えて

　1＋Z＝1－1＋1－1＋1－1＋1－1＋・・・＝Y＝1/2

なので、関数の極限の意味で

　Z＝1/2－1＝－1/2

となっている可能性があります。

実はこの話はゼ－タ関数

　ζ(s)＝1＋1/2^s＋1/3^s＋1/4^s＋1/5^s＋・・・

のs→0での極限値が－1/2であることにつながっています。s＝0での値を

　ζ(0)＝－1/2

と定義すると、ゼ－タ関数はs＝0で滑らかな関数になります。これは

　Z＝1＋1＋1＋1＋1＋・・・＝－1/2

を表しています。

数学というのは登山とよく似ています。知らない山に登るのは大変ですが、その分登頂の絶景には感動します。景色を忘れてしまっても、登頂の達成感は長く心に残ります。数学も同じように、知らない定理を理解するのは大変ですが、その分定理の威力に感動します。もしその定理を忘れてしまっても、理解した達成感は長く心に残ります。登山が遊びなら、数学も遊びなのです。

これまで高次方程式の解を求め、解を表示する拡大体とその上の自己同型群との対応関係を調べてきました。今日はガロアの基本定理を証明します。ガロアの定理は部分群Hが対応する拡大体Bを不変にするとき、拡大体Bは対応する部分群Hの不変体になっており、両者に対応関係があることを示しています。ガロアの定理に従って方程式の解を引き受ける拡大体上の同型写像の群を分解して解析すると、元の方程式が代数的に解けるのかどうかを確かめることができます。

そのための準備として、2つの定理を紹介します。最初の定理はアルティンの定理です。それは『体E上のn個の相異なる同型写像による不変体KからEへの体の拡大次数はn以上である』という主張です。2番目の定理は『先ほどの同型写像が群であれば、拡大次数はちょうど群の要素数に一致する』というものです。これらの定理からガロアの基本定理が証明されます。

 

＜アルティンの定理1＞

体Eから体Fへのn個の相異なる同型写像σ₁、σ₂、・・・σ_nがあるとする。これらの同型写像による不変体KからEへの体の拡大次数はn以上である。

 

同型写像　σ₁、σ₂、・・・σ_n；E　→　F

不変体　K＝｛x∊E｜σ₁(x)＝σ₂(x)＝・・・＝σ_n(x)｝

→　KからEへの体の拡大次数　[E：K]≧n

 

証明）σ₁、σ₂、・・・σ_nが体Eから体Fへのn個の相異なる同型写像であれば、

σ₁、σ₂、・・・σ_nは線形独立です。まずこの事実を証明しましょう。

例えば、n＝2のとき、σ₁≠σ₂より∃α∊E、σ₁(α)≠σ₂(α)。

　x₁σ₁＋x₂σ₂＝0　ならば、任意のx∊Eに対して、x₁σ₁(x)＋x₂σ₂(x)＝0。σ₁(α)を掛け、

   x₁σ₁(α)σ₁(x)＋x₂σ₁(α)σ₂(x)＝0

が成り立ちます。またαx∊Eに対して、x₁σ₁(αx)＋x₂σ₂(αx)＝0。つまり

   x₁σ₁(α)σ₁(x)＋x₂σ₂(α)σ₂(x)＝0

が成り立ちます。上の2式を引き算すると、任意のx∊Eに対して

    (σ₁(α) －σ₂(α))・x₂σ₂(x)＝0。

σ₁(α)≠σ₂(α)なので、x₂＝0となります。代入してx₁＝0も得られます。

   x₁σ₁＋x₂σ₂＝0　ならば、x₁＝x₂＝0

が示されたので、σ₁、σ₂は線形独立です。n＝3の場合も同様にして

　x₁σ₁＋x₂σ₂＋x₃σ₃＝0　ならば、x₁＝x₂＝x₃＝0

が成り立ちます。実際

　x₁σ₁(α)σ₁(x)＋x₂σ₁(α)σ₂(x) ＋x₃σ₁(α)σ₃(x)＝0

　x₁σ₁(α)σ₁(x)＋x₂σ₂(α)σ₂(x) ＋x₃σ₃(α)σ₃(x)＝0

両式を引き算すると、任意のx∊Eに対して、

　(σ₁(α) －σ₂(α))・x₂σ₂(x)＋(σ₁(α) －σ₃(α))・x₃σ₃(x)＝0。

σ₁(α)≠σ₂(α) 、σ₁(α)≠σ₃(α)であり、2つの元σ₂とσ₃は線形独立なので、x₂＝x₃＝0となります。x₂＝x₃＝0を代入して

　x₁σ₁(α)σ₁(x)＝0。

よってx₁＝0も得られます。このようにして、σの元の数をnまで増やすことができます。

次に[E：K]＝r ＜n と仮定すると矛盾が生じることを示します。これは体K上のベクトル空間Eに｛α₁、α₂、・・・α_r｝のr個の基底が存在することを示しています。以下の連立方程式は、

　  σ₁(α₁)x₁＋σ₂(α₁)x₂＋σ₃(α₁)x₃＋・・・＋σ_n(α₁)x_n＝0

      σ₁(α₂)x₁＋σ₂(α₂)x₂＋σ₃(α₂)x₃＋・・・＋σ_n(α₂)x_n＝0

　　・・・・・・・

      σ₁(α_r)x₁＋σ₂(α_r)x₂＋σ₃(α_r)x₃＋・・・＋σ_n(α_r)x_n＝0

方程式の数rが未知数x₁,x₂…,x_nの数nより小さいので自明でない解x₁,x₂…,x_nを持ちます。[E：K]＝rより、体K上のベクトル空間Eの任意の元α∊Eはa_1、a_{2、・・・}a_r ∊Kを用いて

     α＝a₁α₁+a₂α₂+・・・+ a_rα_r

と書けます。上記の方程式にσ₁(a₁)を掛けると

     σ₁(a₁)σ₁(α₁)x₁＋σ₁(a₁)σ₂(α₁)x₂＋・・・＋σ₁(a₁)σ_n(α₁)x_n＝0。

Kは同型写像の不変体だから、

      σ₁(a₁)＝σ₂(a₁) ＝σ₃(a₁) ＝…＝σ_ｎ(a₁)

が成り立つことを利用すると、上式は

       σ₁(a₁)σ₁(α₁)x₁＋σ₂(a₁)σ₂(α₁)x₂＋・・・＋σ_n(a₁)σ_n(α₁)x_n＝0

となります。同型写像ですから

       σ₁(a₁α₁)x₁＋σ₂(a₁α₁)x₂＋σ₃(a₁α₁)x₃・・・＋σ_n(a₁α₁)x_n＝0

が成り立ちます。他の方程式も同様に変形すると

　  σ₁(a₁α₁)x₁＋σ₂(a₁α₁)x₂＋σ₃(a₁α₁)x₃・・・＋σ_n(a₁α₁)x_n＝0

      σ₁(a₂α₂)x₁＋σ₂(a₂α₂)x₂＋σ₃(a₂α₂)x₃・・・＋σ_n(a₂α₂)x_n＝0

      ・・・・・・

       σ₁(a_rα_r)x₁＋σ₂(a_rα_r)x₂＋σ₃(a_rα_r)x₃・・・＋σ_n(a_rα_r)x_n＝0

を得ます。これらの方程式を辺々加えます。第一項の和は

      σ₁(a₁α₁)x₁＋σ₁(a₂α₂)x₁＋・・・＋σ₁(a_rα_r)x₁

   ＝{σ₁(a₁α₁)＋σ₁(a₂α₂)＋・・・＋σ₁(a_rα_r)}x₁

   ＝σ₁(a₁α₁＋a₂α₂＋・・・＋a₂α_r)x₁

   ＝σ₁(α)x₁

となるので、任意の元α∊Eに対して

     σ₁(α)x₁＋σ₂(α)x₂＋σ₃(α)x₃＋・・・＋σ_n(α)x_n＝0

が成り立ちます。σ₁、σ₂、・・・σ_nは相異なる同型写像で、σ_i(α)≠0です。またx₁,x₂…, x_nの中には0でないものが必ず一つはあります。よってσ₁、σ₂、・・・σ_nは線形独立ではありません。これはσ₁、σ₂、・・・σ_nが線形独立であることと矛盾します。つまり[E：K]＝r ＜n という仮定が誤っていたことを示しています。よって    [E：K]≧n  が示されました。証明終わり。

アルティンの定理では｛σ₁、σ₂、・・・σ_n｝が群を成すと仮定していません。実際｛σ₁、σ₂、・・・σ_n｝が群を成さないのであれば、あるσ_i^-1、かσ_iσ_jが｛σ₁、σ₂、・・・σ_n｝以外の元になります。x∊Kに対して、 (σ_iσ_j) (x)＝σ_i(σ_j (x))＝σ_i(x)＝xとなり、不変体 K＝｛x∊E｜σ₁(x)＝σ₂(x)＝・・・＝σ_n(x)＝σ_iσ_j(x)＝x ｝を構成する相異なる自己同型写像｛σ₁、σ₂、・・・σ_n、σ_iσ_j｝はn+1個になります。あるいは、x＝e(x)＝(σ_i^-1σ_i) (x)＝σ_i^-1(σ_i(x) )＝σ_i^-1(x )となり、不変体 K＝｛x∊E｜σ₁(x)＝σ₂(x)＝・・・＝σ_n(x)＝σ_i^-1(x)＝x｝を構成する相異なる自己同型写像｛σ₁、σ₂、・・σ_n、σ_i^-1｝はn+1個になります。よって[E：K]≧n+1 となります。不変体 Kを構成する自己同型写像｛σ₁、σ₂、・・・σ_n｝が群をなしていれば、演算で新しい元は生成しません。不変体 Kを構成する自己同型写像はn個に限られるので[E：K]＝nとなります。それを保証するのが次の定理です。

定理2

体E上のn個の相異なる自己同型写像σ₁、σ₂、・・・σ_nが群Gをなす場合、群Gの不変体Kから体Eへの拡大次数はnとなる。

自己同型写像　σ₁、σ₂、・・・σ_n；E　→　E

群G＝｛σ₁、σ₂、・・・σ_n｝

不変体 K＝｛x∊E｜σ₁(x)＝σ₂(x)＝・・・＝σ_n(x)｝

→　KからEへの体の拡大次数　[E：K]＝n

注意）標数0の体に限定する。標数nとは、n・1＝0を満たす数。複素数体は標数0。

証明）[E：K]≦nを示せれば、前定理[E：K]≧nと合わせて、[E：K]＝nとなります。

任意のx∊Eに対して、トレ－ス

     S(x)＝σ₁(x)＋σ₂(x)＋・・・σ_n(x) ∊E

を定義します。｛σ₁、σ₂、・・・σ_n｝は群を成しているので、任意のi＝1,2、…nに対して、

      σ_i・｛σ₁、σ₂、・・・σ_n｝＝｛σ₁、σ₂、・・・σ_n｝

です。従って

　σ_i(S(x))＝σ_iσ₁(x)＋σ_iσ₂(x)＋・・・σ_iσ_n(x)＝σ₁(x)＋σ₂(x)＋・・・σ_n(x)＝S(x)

であるから、S(x) ∊Kとなります。K係数のベクトル空間Eの次元がｎ以下であることを示すために、ベクトル空間Eのn+1個の基底｛α₁,α₂,…α_n,α_n+1｝が一次独立ではないことを示せばよいです。Gは群であるために、σ_i^-1∊Gが存在します。連立方程式

　σ₁^-1(α₁) x₁＋σ₁^-1(α₂) x₂＋・・・＋σ₁^-1(α_n) x_n＋σ₁^-1(α_n+1) x_n+1＝0

    σ₂^-1(α₁) x₁＋σ₂^-1(α₂) x₂＋・・・＋σ₂^-1(α_n) x_n＋σ₂^-1(α_n+1) x_n+1＝0

　  ・・・・・・・・・・・・・・

     σ_n^-1(α₁) x₁＋σ_n^-1(α₂) x₂＋・・・＋σ_n^-1(α_n) x_n＋σ_n^-1(α_n+1) x_n+1＝0

に関して、未知数x₁,x₂…,x_n+1の個数ｎ＋1は式の個数ｎより大きいので、x₁,x₂…,x_n+1はx₁＝x₂＝…＝x_n+1＝0の自明な解以外の少なくとも一つはゼロではない非自明解を持ちます。非自明解をx₁≠0とすると、x₁≠0で全体を割ることで、x₁＝1として良いです。i番目の方程式にσ_iを作用させると、

       σ_i (σ_i^-1(α₁) x₁) ＋σ_i (σ_i^-1(α₂) x₂)＋・・・＋σ_i(σ_i^-1(α_n+1) x_n+1)＝0

　　α_1・σ_i(x₁)＋α_2・σ_i(x₂) ＋・・・＋α_n+1・σ_i (x _n+1) ＝0

となります。これをすべての方程式について行うと

        α_1・σ₁(x₁)＋α_2・σ₁(x₂) ＋・・・＋α_n+1・σ₁(x _n+1) ＝0

        α_1・σ₂(x₁)＋α_2・σ₂(x₂) ＋・・・＋α_n+1・σ₂(x _n+1) ＝0

　　　・・・・・・・・・・・・・・　

　     α_1・σ_n(x₁)＋α_2・σ_n(x₂) ＋・・・＋α_n+1・σ_n(x _n+1) ＝0

を得ます。辺々を加えると、S(x)＝σ₁(x)＋σ₂(x)＋・・・σ_n(x) ∊Kを用いると

         S(x₁)α₁＋S(x₂)α₂ ＋・・・＋S(x _n+1)α_n+1＝0

S(x_i)∊K、つまりS(x₁)、S(x₂)、・・・S(x _n+1)はK係数であります。

｛α₁,α₂,…α_n,α_n+1｝が一次独立ならば、S(x₁)＝S(x₂)＝・・・＝S(x _n+1)＝0

です。しかし

      S(x₁)＝S(1)＝σ₁(1)＋σ₂(1)＋・・・＋σ_n(1)＝1+1+・・・+1＝n≠0

ので、ベクトル空間Eのn+1個の基底｛α₁,α₂,…α_n,α_n+1｝が一次独立ではないことが示されました。ベクトル空間Eの次元はn次元以下 [E：K]≦nが示されました。前定理[E：K]≧nと合わせて、拡大体の次数は[E：K]＝nとなります。証明終わり。

＜ガロアの基本定理＞

[1]EをKの正規拡大体、そのK自己同型群Aut_K(E)をGとする。E⊃B⊃Kなる中間体Bを不変にするGの部分群H＝｛σ∊G｜∀x∊B、σ(x)＝x｝があれば、

(1)EはBの正規拡大体である。

(2)HがBのK自己同型群である。

(3)中間体Bと群Hは一対一に対応する。

[2] HがGの正規部分群であれば、

(1)BはKの正規拡大体である。

(2) G/HがBのK自己同型群である。

(3)体Kと余剰群G/H一対一に対応する。

注意1）x∊Bにおいて、任意のσ₁,σ₂∊Hに対して、σ₁σ₂(x)＝σ₁(σ₂(x))＝σ₁(x)＝xより、σ₁σ₂∊H。またσ₁(x)＝xよりx＝σ₁^-1σ₁ (x)＝σ₁^-1 (x)なので、σ₁^-1∊Hとなります。よってHの定義からHはすでに群になっています。

注意2）EはBの正規拡大体であるとは、BがE上の自己同型写像の作る群Hの不変体になっていることです。このとき[E；B]＝＃(H)が成り立ちます。

注意3）Hが正規部分群であれば、G/Hは群になります。Hが正規部分群でなければ、G/Hは群になりません。

[1] (1) EはBの正規拡大体であることの証明）

Hの要素数を＃(H)＝rとすると、群H＝｛σ∊G｜∀x∊B、σ(x)＝x｝の定義から∀x∊Bに対して、σ₁,σ₂,…σ_r ∊H⊂G、σ₁(x)＝σ₂(x)＝…＝σ_r(x)＝xが成り立つので、定理2より[E；B]＝rが成り立ちます。次にBはHの不変体であることを示します。Hの不変体をB’＝｛x∊E｜∀σ∊H、σ(x)＝x｝とします。Bの定義から∀x∊Bに対して、∀σ∊H、σ(x)＝xなので、B’の定義からx∊B’が成り立ちます。よってB’⊃Bです。Hは群であり、B’はHの不変体なので、定理2より[E；B’]＝rが成り立ちます。[E；B]＝[E；B’]かつB’⊃Bより、B＝B’となります。つまりBがE上の自己同型写像の作る群Hの不変体になっており、[E；B]＝＃(H)が成り立つので、EはBの正規拡大体であることが示されます。証明終わり。

[1] (2) HがBのK自己同型群であることの証明）

＃(G/H)＝sとすると、ラグランジュの定理より、N＝＃(G)＝＃(H) -＃(G/H)＝r・sです。σ、σ’∊Gが同じ剰余類G/Hに属するとすると、σ^-1σ’ ∊Hとなります。H＝｛σ∊G｜∀x∊B、σ(x)＝x｝の定義より、∀x∊Bに対して、σ^-1σ’(x)＝x、すなわちσ’(x)＝σ(x)です。つまり同じ剰余類G/Hに属するσはB上で同じ同型写像を与えます。σ∊GはE上のK自己同型写像ですが、これをB上に限定すると、＃(G/H)＝sより、BからEへの相異なるs個のK同型写像が存在します。

[1] (3) 中間体Bと群Hは一対一に対応することの証明）

Hが正規部分群でなければ、G/Hは群にならないので、アルティンの定理より[B：K]≧sとなります。n＝[E：K] ＝[E：B] [B：K] ≧rs＝n、[B：K]≧sより[B：K]＝sとなります。つまりBの基底s個とB上の同型写像の個数s∊G/Hは対応しています。群Gを中間体Bで制限した群G^B＝｛σ∊G｜∀x∊B⊂E、σ(x)＝x｝をHとすることで、中間体Bが体Eを部分群Hで制限した体E^H＝｛x∊E｜∀σ∊H⊂G、σ(x)＝x｝となるので、中間体Bと部分群Hは一対一に対応します。

・HがGの正規部分群であるとき、

[2] (1)BはKの正規拡大体であることの証明）

BはKの正規拡大体であるとは、KがB上の自己同型写像の作る群G/Hの不変体になっていることです。σがB上の自己同型写像であるとは、σ(B)＝Bということです。このとき[B；K]＝＃(G/H)が成り立ちます。H＝｛σ∊G｜∀x∊B、σ(x)＝x｝と定義されています。E上の自己同型写像σ∊Gに対して、σ(B)⊂Eです。中間体σ(B)を不変にする群はσHσ^-1になっています。なぜならば、τ∊σHσ^-1⇔　σ^-1τσ∊H　であることはHの定義により任意のx∊Bにおいて、σ^-1τσ(x)＝x　　⇔　τσ(x)＝σ(x)　すなわちτ(σ(B))＝σ(B)を意味するからです。Hが正規群であれば、任意のσ∊Gに対して、σHσ^-1＝Hです。今Hが正規群なので、τ∊Hに対してτ(σ(B))＝σ(B)、すなわちσ(B)はHの不変体になっています。先ほどHの不変体はBであることを証明したので、σ(B)＝B⊂Eが示されました。中間体Bは群G/H＝σHσ^-1の不変体になっているので、BはKの正規拡大体です。逆に任意のσ∊Gに対して、σ(B)＝Bならば、τ∊σHσ^-1に対してτ(B)＝Bとなります。これはσHσ^-1＝HすなわちHはGの正規部分群であることを意味します。

[2] (2) G/HがBのK自己同型群であることの証明）

任意のx∊Bにおいて、σ(x)＝σ’(x)　⇔　σ’^-1σ(x)＝xとなり、σ’^-1σ∊Hとなります。これはσ’、σが同じG/Hの類に属していることを意味するので、Aut_K(B)＝G/Hです。証明終わり。

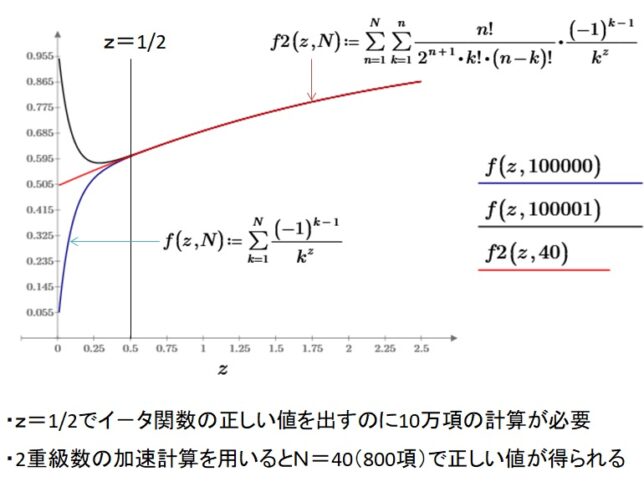
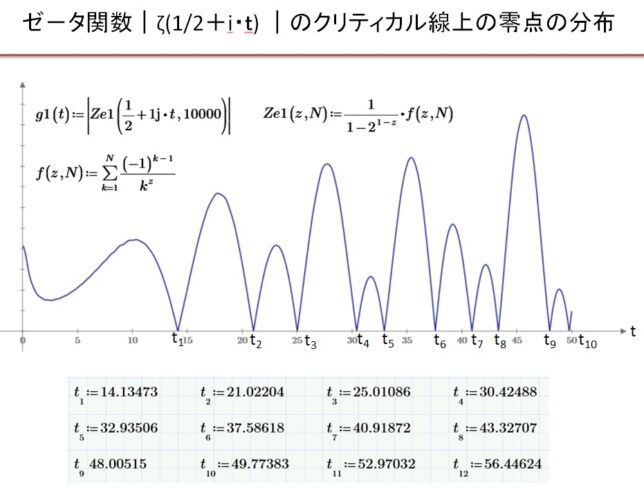
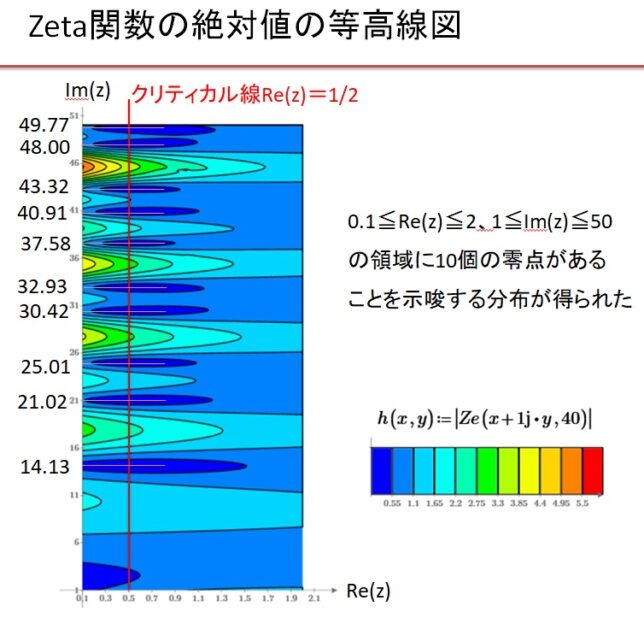
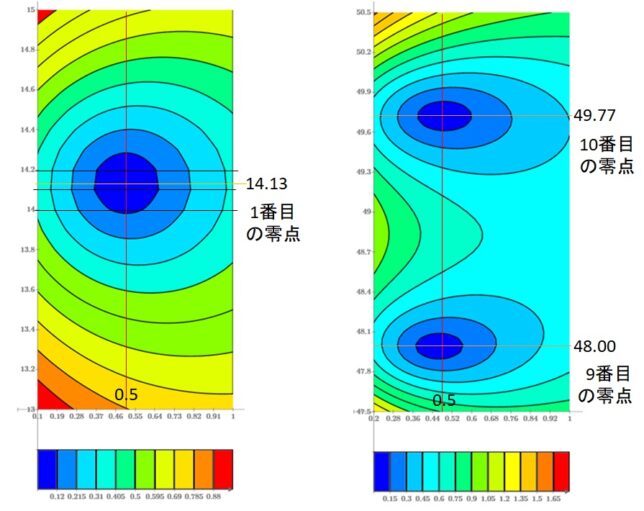
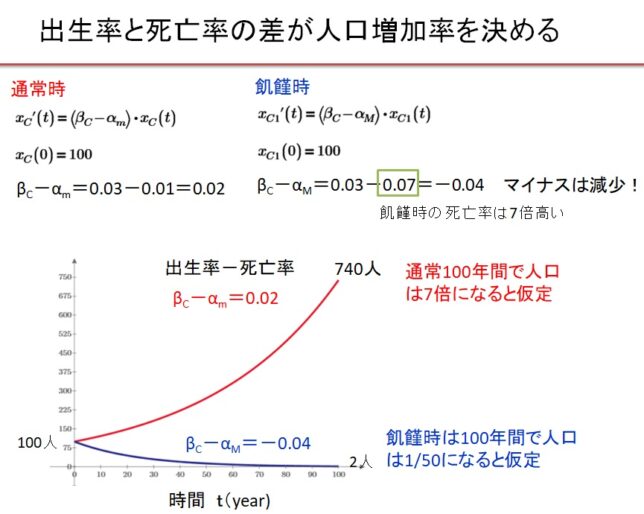
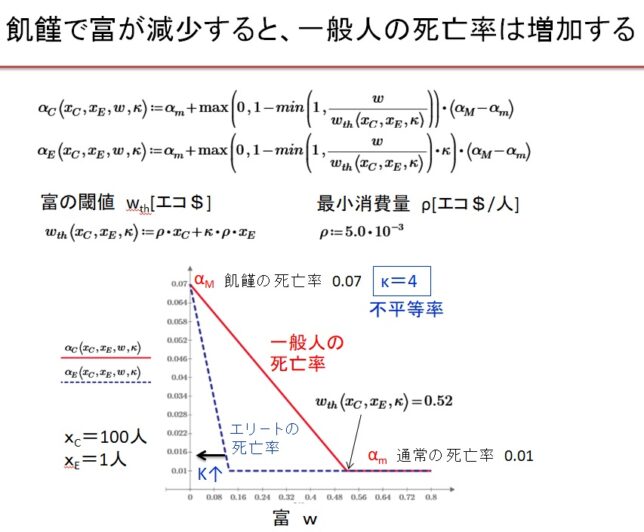
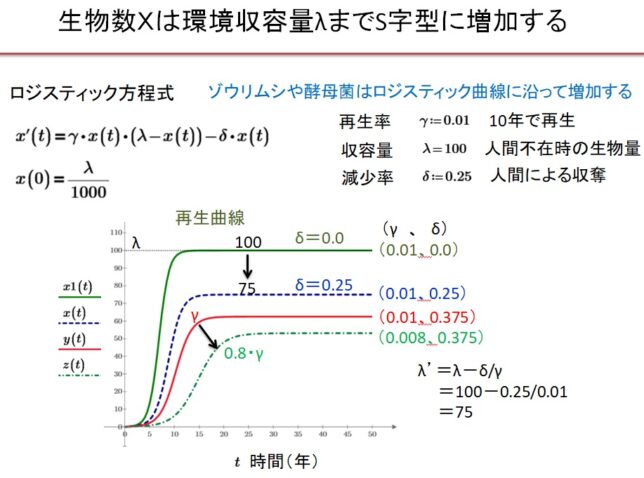
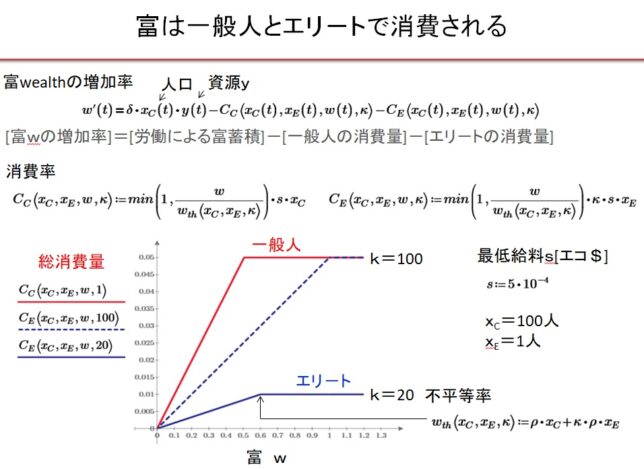
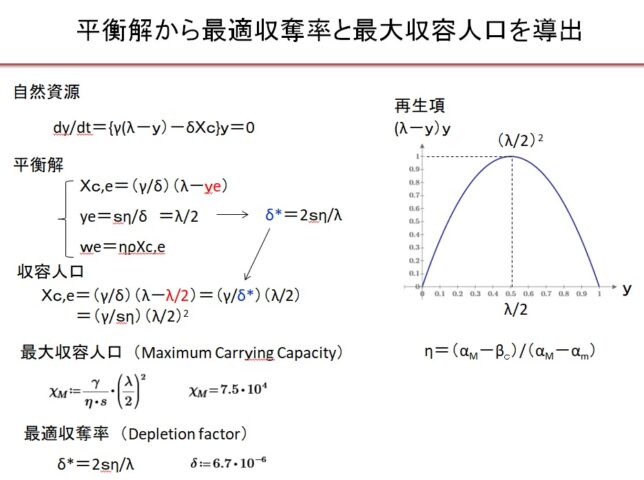
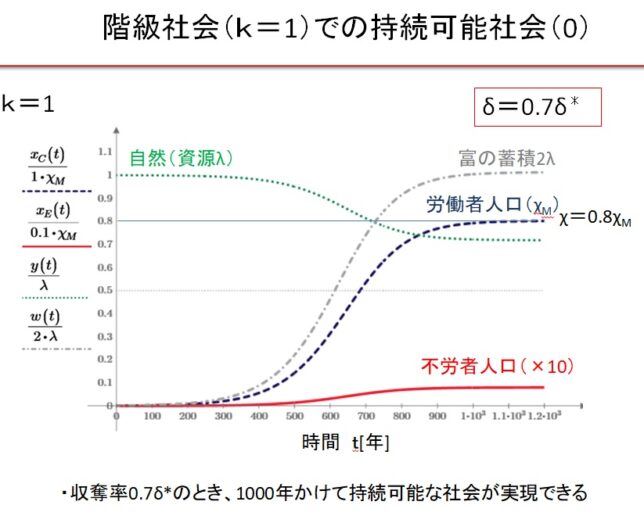
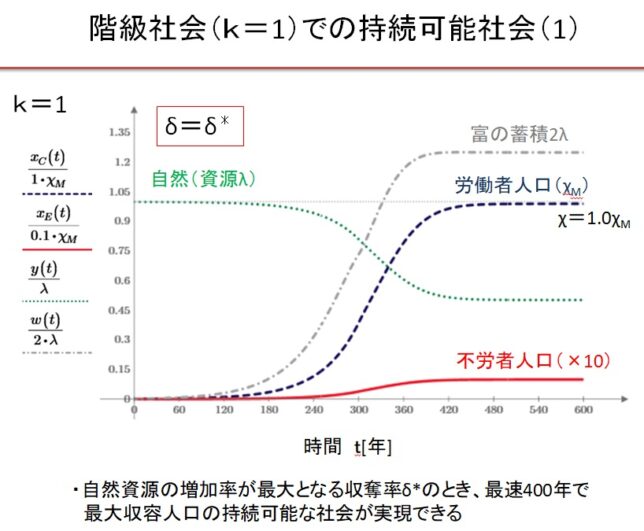
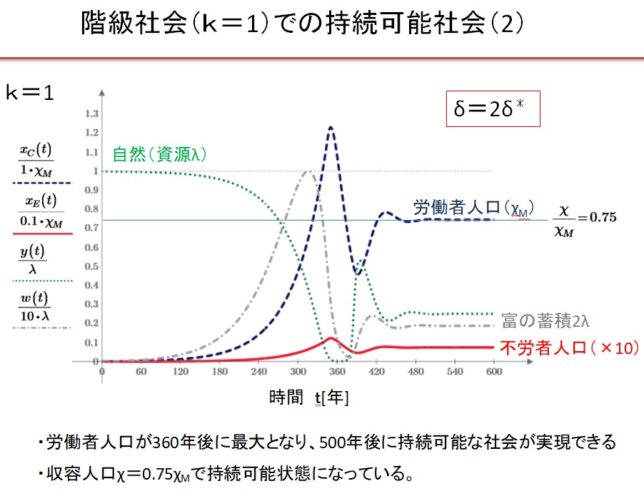
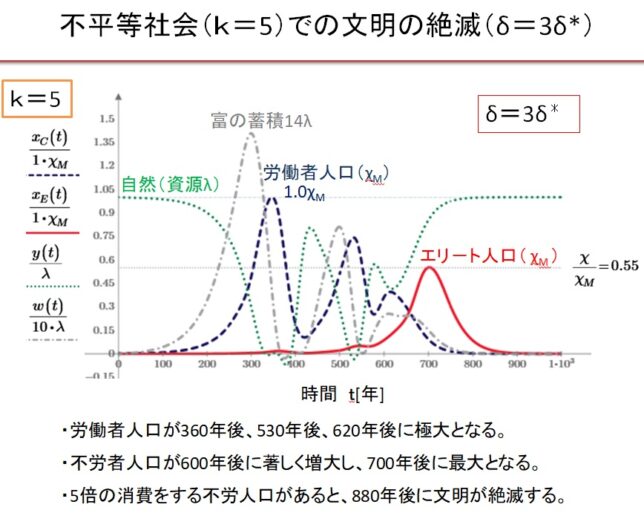
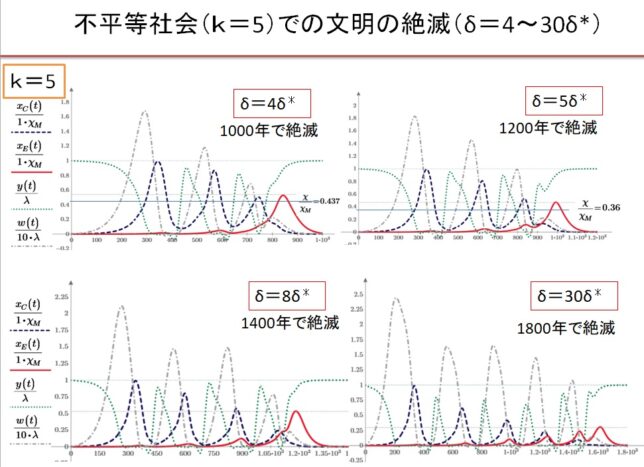
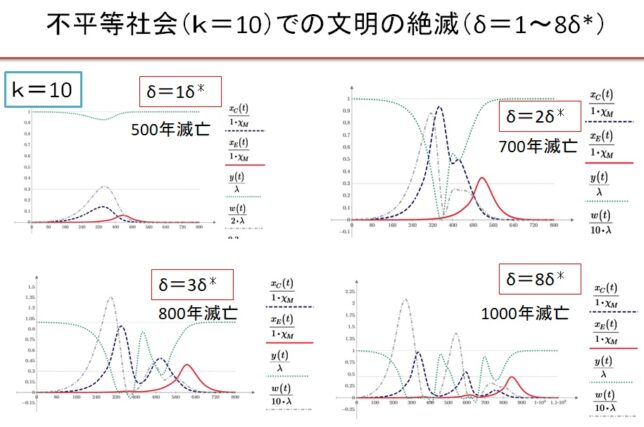
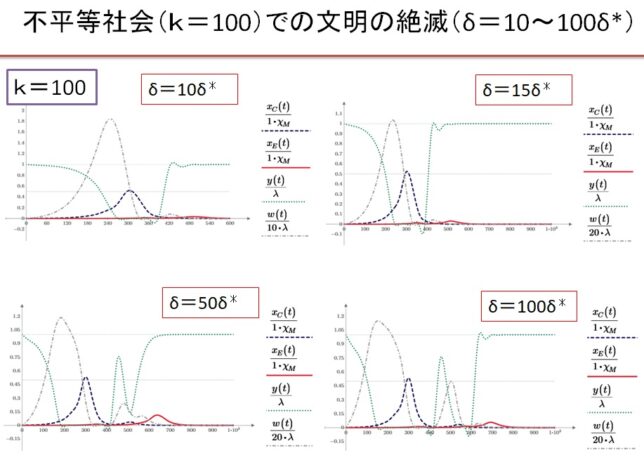
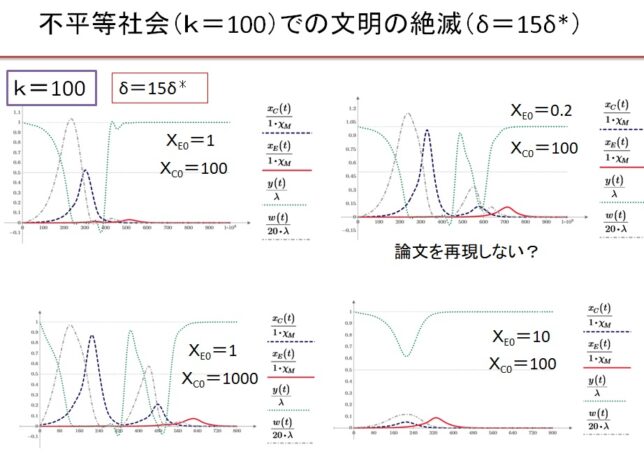
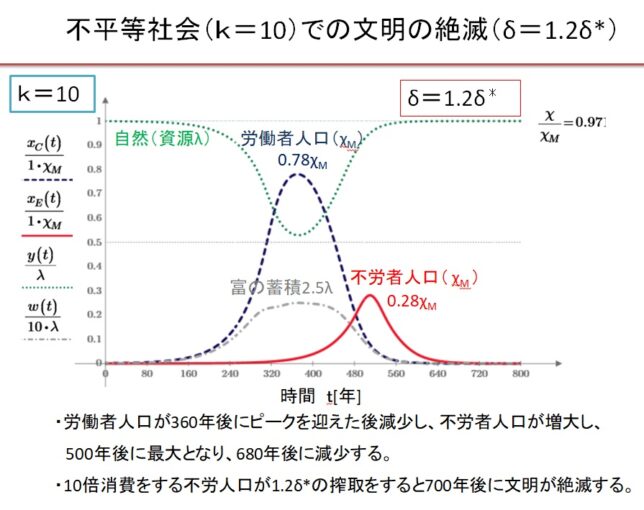
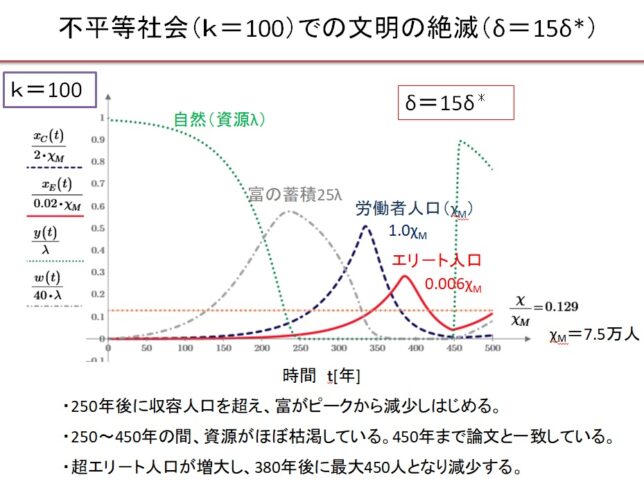
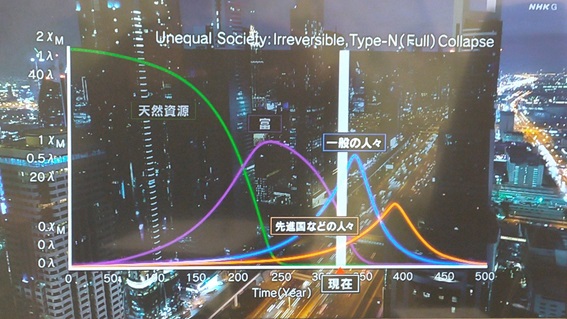
前回はf(x)＝x³－2を例に、f(x)の分解体とガロア群を求めました。今回は多項式の次数を1つ上げて、拡大体の列と対応するガロア群の列を導出します。

Ex.3　　Q多項式f(x)＝x⁴－3を例に、f(x)の分解体とガロア群を求めてみましょう。

f(x)を因数分解すると

• f(x)＝x⁴－3＝(x²－⁴√9) ( x²＋⁴√9)＝(x－⁴√3) ( x＋⁴√3) ( x－⁴√3i) ( x＋⁴√3i)、
• i²＝－1、i³＝－i、i⁴＝1

となります。f(x)＝0の4つの解は、

• α₁＝⁴√3、α₂＝－⁴√3、α₃＝⁴√3i、α₃＝－⁴√3i

となります。f(x)の分解体は4つの解をQに付け加えたものですが、⁴√3とiの2つを付け加えることに等しいので、f(x)の分解体はQ(⁴√3,i)となります。⁴√3をべき乗してゆくと、

1． ⁴√3、⁴√9、⁴√27の4つの基底が得られます。a_0、a_{1、・・・}a₇ ∊Q（有理数）を用いて、

・　Q(⁴√3、i)＝｛a₀＋a_1・⁴√3＋a_2・⁴√9＋a_3・⁴√27＋a₄i＋a_5・⁴√3i＋a_6・⁴√9i ＋a_7・⁴√27i｝

と書けます。体の拡大の次数は8となります。

• [Q(⁴√3、i)：Q]＝[Q(⁴√3、i)：Q(⁴√3)]・[Q(⁴√3)：Q]＝2・4＝8

拡大体Q(⁴√3、i)上のQ自己同型写像σ∊Aut_Q(Q(⁴√3、i))を求めます。σは同型なので

• σ(ab)＝σ(a)・σ(b)、σ(a＋b)＝σ(a)＋σ(b)　for a,b∊Q

を満たします。またσは3∊Qを不変に保つので

• 3＝σ(3)＝σ( (⁴√3)⁴) ＝σ(⁴√3) ⁴

となります。σを⁴√3にiを掛ける作用とiを不変にする作用を持つ写像

• σ(⁴√3)＝⁴√3i、σ(i)＝i

だとすると、上式を満たす4つの写像は、

σ(⁴√3)＝⁴√3i、σ²(⁴√3)＝⁴√3ii＝－⁴√3、σ³(⁴√3)＝⁴√3iii＝－⁴√3i、σ⁴(⁴√3)＝⁴√3

と表現できます。σ⁴は恒等写像です。また―1∊Qを不変に保つ写像をτとすると

• －1＝τ(－1)＝τ(ii)＝τ(i)²

なので、τはiに－1を掛ける作用と⁴√3を不変にする作用を持つ写像

• τ(i)＝－i、τ(⁴√3)＝⁴√3

だとします。τ²(i)＝iなのでτ²は恒等写像です。Q(⁴√3、i)/Q上のガロア群Gは

• G＝Gal(Q(⁴√3、i)/Q)＝｛e、σ、σ²、σ³、τ、στ、σ²τ、σ³τ｝、＃(G)＝8

となります。Gの位数は8となり、体の拡大の次数8と一致します。これらの写像は

• τσ²(⁴√3)＝τ(－⁴√3)＝－⁴√3、σ²τ(⁴√3)＝σ²(⁴√3)＝－⁴√3
• στσ(⁴√3)＝στ(⁴√3i)＝σ(－⁴√3i) ＝－⁴√3ii＝⁴√3＝τ(⁴√3)
• τστ(⁴√3)＝τσ(⁴√3) ＝τ(⁴√3i)＝－⁴√3i、σ³(⁴√3)＝⁴√3iii＝－⁴√3i

であるから、

• τσ²＝σ²τ　⇔　σ^－2(σ²τ) σ^－2＝σ²τ
• στσ＝τ、τ^－1＝τ、τστ＝σ³　⇔　(τσ)^－1＝τσ

なる性質があります。これらから

• στ・σ²τ＝στ・τσ²＝σ³
• στ・σ³τ＝στσ・σ²τ＝τσ²τ＝σ²
• τ・σ²τ＝τσ²・τ＝σ²τ・τ＝σ²
• τ・σ³τ＝τσ²・στ＝σ²τ・στ＝σ²・τστ＝σ²・σ³＝σ・σ⁴＝σ
• σ³τ・σ³τ＝σ³・σ＝e
• σ²τ・σ³τ＝σ²・σ＝σ³
• σ²τ・σ²τ＝σ²τ・τσ²＝σ
• σ²・τ＝σ・ττ・στ＝στσ³＝ττστσ³＝τσ³σ³＝τσ²
• σ²・τσ＝σ・στσ＝στ＝τστ＝τσ³
• σ²・τσ²＝τσ³σ＝τ
• σ³・τ＝στσ²＝τσ
• σ³・τσ＝τσ²

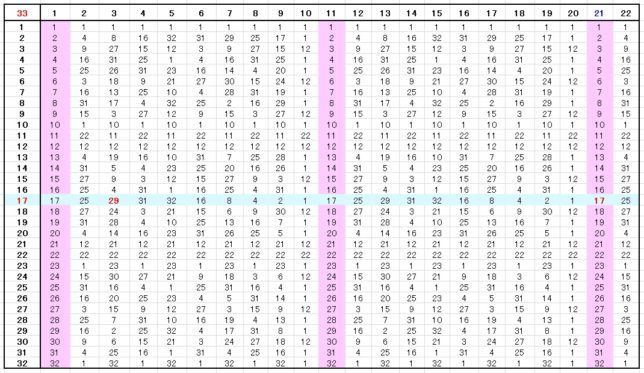
が成り立ちます。8つの元同士の演算の結果を次の演算表にまとめました。

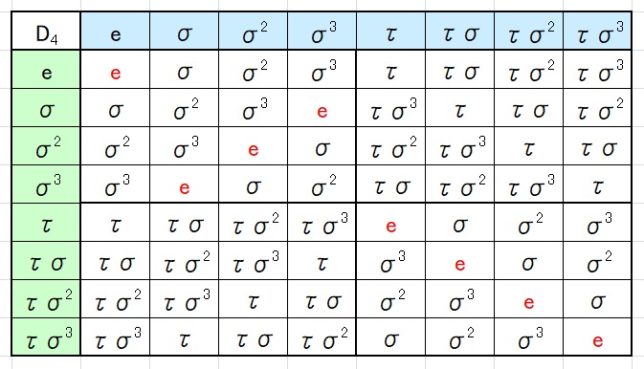
ここで

• τ（縦の元）・σ（横の元）＝τσ（表中の元）
• σ（縦の元）・τ（横の元）＝τσ³（表中の元）

に注意して下さい。τσⁿの逆元はτσⁿになっていることが分かります。8個の元同士の演算が8個の元で閉じているので、Gは群になっています。これはD₄と呼ばれ、四角板の1/4回転と反転操作のなす群に相当します。

f(x)の分解体Q(⁴√3,i)上のQ自己同型写像全体は8次のD₄群となりました。

• D₄＝｛e、σ、σ²、σ³、τ、τσ、τσ²、τσ³｝

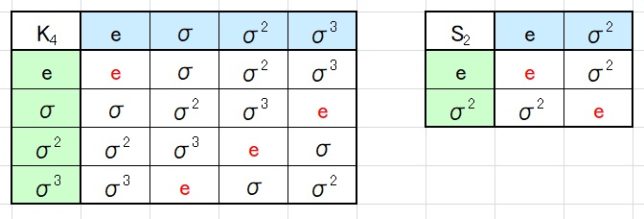
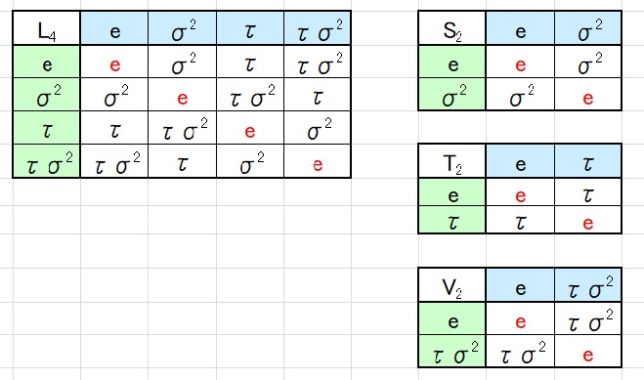
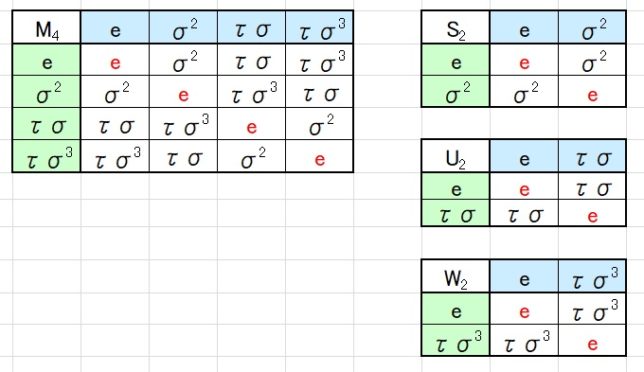
Q自己同型写像というのは、有理数体Qは不変に保つQ(⁴√3,i)からQ(⁴√3,i)への全単射写像という意味です。次にD₄の部分群を調べます。4次の部分群はK₄、L₄、M₄の3つがあります。

• K₄＝｛e、σ、σ²、σ³｝＝Z/4Z
• L₄＝｛e、σ²、τ、τσ²｝＝Z/2Z×Z/2Z
• M₄＝｛e、σ²、τσ、τσ³｝＝Z/2Z×Z/2Z

2次の部分群はS₂、T₂、U₂、V₂、W₂の5つがあります。

・　S₂＝｛e、σ²｝、T₂＝｛e、τ｝、U₂＝｛e、τσ｝、V₂＝｛e、τσ²｝、W₂＝｛e、τσ³｝

｛e、τσ^k｝（k＝0,1,2,3）は4つの2次の部分群を作ります。自明な1次の部分群

・　I＝{e}

があります。

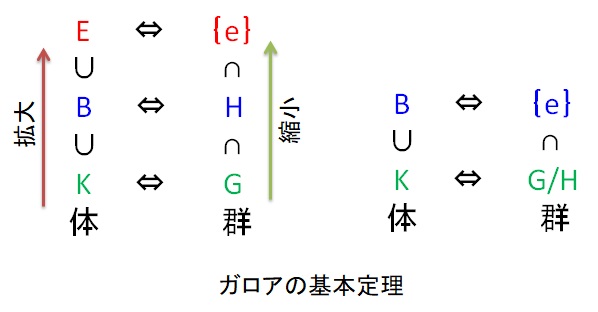
ガロア群の包含関係は7種類あります。7種類の群の系列に対応する拡大体の系列を示します。

• D₄⊃K₄⊃S₂⊃I　　

         Q⊂Q(i)⊂Q(√3,i)⊂Q(⁴√3,i)

• D₄⊃L₄⊃S₂⊃I

         Q⊂Q(√3)⊂Q(√3,i)⊂Q(⁴√3,i)

• D₄⊃L₄⊃T₂⊃I

         Q⊂Q(√3)⊂Q(⁴√3)⊂Q(⁴√3,i)

• D₄⊃L₄⊃V₂⊃I

         Q⊂Q(√3)⊂Q(⁴√3i)⊂Q(⁴√3,i)

• D₄⊃M₄⊃S₂⊃I

         Q⊂Q(√3i)⊂Q(√3,i)⊂Q(⁴√3,i)

• D₄⊃M₄⊃U₂⊃I

         Q⊂Q(√3i)⊂Q((1－i)-⁴√3)⊂Q(⁴√3,i)

• D₄⊃M₄⊃W₂⊃I

         Q⊂Q(√3i)⊂Q((1＋i)-⁴√3)⊂Q(⁴√3,i)

[1]　K₄＝Gal(Q(i)/Q)を示します。a₀,a_1、、、a₇∊Qに対して、x=⁴√3とおきます。                   _、

X＝a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ ∊Q(x,i)

σ∊K₄に対して、σ(X)＝Xとなる係数の条件を求めます。σ(x)＝ix、σ(i)＝iです。

　σ(a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ )

＝a₀+ a₁xi－a₂x²－a₃ix³+ a₄i－a₅x－a₆ix²+ a₇ x³

• a₁＝－a₅、a₂＝－a₂＝0、a₃＝a₇、a₅＝a₁、a₆＝－a₆＝0、a₇＝－a₃、

→　a₁＝a₂＝a₃＝a₅＝a₆＝a₇＝0

　　X＝a₀+ a₄i∊Q(i)

K₄＝｛e、σ、σ²、σ³｝の全ての元に対して、σ(X)＝Xが成り立つので、K₄は拡大体Q(i)/Q上のガロア群になっています。Q(i)はK₄の不変体になっています。

D₄⊃K₄⊃S₂⊃I　　⇔　　Q⊂Q(i)⊂Q(√3,i)⊂Q(⁴√3,i)

• S₂＝｛e、σ²｝＝Gal(Q(√3、i)/Q)を示します。
• σ²(a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ )

＝σ(a₀+ a₁xi－a₂x²－a₃ix³+ a₄i－a₅x－a₆ix²+ a₇ x³)

　　＝a₀－a₁x＋a₂x²－a₃x³+ a₄i－a₅ix＋a₆ix²－a₇ix³

　　a₁＝－a₁、a₃＝－a₃＝0、a₅＝－a₅、a₇＝－a₇、→　a₁＝a₃＝a₅＝a₇＝0

　　X＝a₀＋a₂x² + a₄i＋a₆ix²＝a₀＋a₂√3 + a₄i＋a₆√3 i　∊Q(√3、i)

S₂＝｛e、σ²｝の全ての元に対して、σ²(X)＝Xが成り立つので、S₂は拡大体Q(√3、i)上のガロア群になっています。K₄はD₄の正規部分群、S₂はK₄の正規部分群になっています。

Q(√3、i)は、｛1、√3、i、√3i｝の4つの基底からなる4次元ベクトル空間と同型です。

Q(i)は、｛1、i｝の2つの基底からなる2次元ベクトル空間と同型です。

• D₄⊃K₄⊃S₂⊃I　　⇔　Q⊂Q(i)⊂Q(√3,i)⊂Q(⁴√3,i)
• [Q(⁴√3、i)：Q]＝[Q(⁴√3、i)：Q(√3、i)]・[Q(√3、i)：Q(i)]・[Q(i)：Q]＝2・2・2＝8
• ＃(D₄)＝＃(K₄)・＃(S₂)・＃(I)＝4・2・1＝8

[2] L₄＝｛e、σ²、τ、τσ²｝＝Gal(Q(√3)/Q)を示します。τ(i)＝－i

σ²(X)＝Xより、X＝a₀＋a₂x² + a₄i＋a₆ix²

τ(X)＝τ(a₀＋a₂x² + a₄i＋a₆ix²)＝a₀＋a₂x² －a₄i－a₆ix²＝a₀＋a₂x² + a₄i＋a₆ix²

• －a₄＝a₄＝0、－a₆＝a₆＝0　→　X＝a₀＋a₂x² ＝a₀＋a₂√3　∊Q(√3)

従ってQ(√3)はL₄の不変体になっており、以下のガロア対応が成り立ちます。

• D₄⊃L₄⊃S₂⊃I　⇔　Q⊂Q(√3)⊂Q(√3,i)⊂Q(⁴√3,i)
• [Q(⁴√3、i)：Q]＝[Q(⁴√3、i)：Q(√3、i)]・[Q(√3、i)：Q(√3)]・[Q(√3)：Q]＝2・2・2＝8
• ＃(D₄)＝＃(L₄)・＃(S₂)・＃(I)＝4・2・1＝8

[3] T₂＝｛e、τ｝＝Gal(Q(⁴√3))

• τ(a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ )

＝a₀+ a₁x+ a₂x²+ a₃x³－a₄i－ix－ix²－ix³＝X

　　　a₄＝a₅＝a₆＝a₇＝0　

→　X＝a₀+ a₁x+ a₂x²+ a₃x³＝a₀+ a₁–⁴√3+ a_2-⁴√9+ a₃⁴√27　∊Q(⁴√3)

D₄⊃L₄⊃T₂⊃I　　⇔　Q⊂Q(√3)⊂Q(⁴√3)⊂Q(⁴√3,i)

[4] V₂＝｛e、τσ²｝＝Gal(Q(⁴√3i)/Q)を示します。

• τσ² (a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ )

＝τ(a₀－a₁x＋a₂x²－a₃x³+ a₄i－a₅ix＋a₆ix²－a₇ix³)

＝a₀－a₁x＋a₂x²－a₃x³－a₄i＋a₅ix－a₆ix²+a₇ ix³＝X

　　a₁＝a₃＝a₄＝a₆＝0

　　→　X＝a₀+ a₂x²+a₅ix+ a₇ ix³＝a₀－a₂(⁴√3i)²+a₅(⁴√3i)－a₇(⁴√3i)³ ∊Q(⁴√3i)

D₄⊃L₄⊃V₂⊃I　　⇔　Q⊂Q(√3)⊂Q(⁴√3i)⊂Q(⁴√3,i)

[5] M₄＝｛e、σ²、τσ、τσ³｝＝Gal(Q(√3i)/Q)を示します。

・　σ²(X)＝Xより、X＝a₀＋a₂x² + a₄i＋a₆ix²

　　τσ(X)＝τσ(a₀＋a₂x² + a₄i＋a₆ix²)

　　　　　＝τ(a₀－a₂x² + a₄i－a₆ix²)

　　　　　＝a₀－a₂x²－a₄i＋a₆ix²＝a₀＋a₂x² + a₄i＋a₆ix²＝X

　　　    a₂＝a₄＝0　　→　X＝a₀＋a₆ ix²＝a₀＋a₆ √3i ∊ Q(√3i)

  D₄⊃M₄⊃S₂⊃I  ⇔　Q⊂Q(√3i)⊂Q(√3,i)⊂Q(⁴√3,i)

[6] U₂＝｛e、τσ｝＝Gal(Q((1－i)-⁴√3)) を示します。

・　τσ(X)＝τσ(a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³)

　　　　　＝τ(a₀+ a₁xi－a₂x²－ia₃x³+ a₄i－a₅x－a₆ix²+ a₇ x³)

　　　　　＝a₀－a₁xi－a₂x²＋ia₃x³－a₄i－a₅x＋a₆ix²+ a₇ x³＝X

　　　　a₁＝－a₅、a₂＝a₄＝0、a₃＝a₇、

　　　　　　→　X＝a₀+ a₁x+ a₃x³－a₁ix+a₆ix²+ a₃ ix³

　　　　　　　　　＝a₀+ a₁(1－i)x+ a₃(1＋i)x³+a₆ix²

　(1－i)²＝1－1－2i＝－2i、(1－i)³＝－2i(1－i)＝－2(i＋1)

X＝a₀+ a₁(1－i)x－1/2-a₃(1－i)³-x³－1/2-a₆(1－i)²-x² ∊ Q((1－i)-⁴√3))

• 　D₄⊃M₄⊃U₂⊃I　⇔　Q⊂Q(√3i)⊂Q((1－i)-⁴√3)⊂Q(⁴√3,i)

[7] W₂＝｛e、τσ³｝＝Gal(Q((1+i)-⁴√3)) を示します。

σ(x)＝ix、τ(x)＝x、σ(i)＝i、τ(i)＝－i、x＝⁴√3に注意して

　　σ²(X)＝Xより、X＝a₀＋a₂x² + a₄i＋a₆ix²

　　τσ³(X)＝τσ(a₀＋a₂x² + a₄i＋a₆ix²)　

　　　　　　＝τ(a₀－a₂x² + a₄i－a₆ix²)　

　　　　　　＝a₀－a₂x² －a₄i＋a₆ix²＝X＝a₀＋a₂x² + a₄i＋a₆ix²

　　　　　　a₂＝a₄＝0．　X＝a₀＋a₆ix²

　　(1＋i)²＝1－1＋2i＝2i、i＝1/2-(1＋i)²

　　　X＝a₀＋1/2-a₆ (1＋i)²x² ∊ Q((1＋i)-⁴√3)

• 　D₄⊃M₄⊃W₂⊃I　⇔　Q⊂Q(√3i)⊂Q((1＋i)-⁴√3)⊂Q(⁴√3,i)

ガロア群D₄が4つの解(1234)をどのように置換するかを調べます。

• D₄＝｛e、σ、σ²、σ³、τ、τσ、τσ²、τσ³｝

　＝｛e、(1324)、(12)(34)、(1423)、(34)、(14)(23)、(12)、(13)(24)｝

と表すことができます。

• f(t)＝t⁴－3＝(t²－⁴√9) ( t²＋⁴√9)＝(t－⁴√3) ( t＋⁴√3) ( t－⁴√3i) ( t＋⁴√3i)＝0

の4つの解は、改めてx=⁴√3とおくと

• （α₁、α₂、α₃、α₄）＝(x、－x、ix、－ix)と書けます。

σ(x)＝ix、τ(x)＝x、σ(i)＝i、τ(i)＝－i、の規則で4つの解を変換すると

• σ(x、－x、ix、－ix)＝(ix、－ix、－x、x)

⇔　σ(α₁、α₂、α₃、α₄)＝(α₃、α₄、α₂、α₁)

⇔　σ＝(1→3→2→4→1)＝(1324)

すなわちσは(1324)の置換作用素となっています。同様にして

• σ²(x、－x、ix、－ix)＝σ(ix、－ix、－x、x)＝(－x、x、－ix、ix)＝(α₂,α₁,α₄,α₃)

　　σ²＝(1→2→1、3→4→3)＝(12)(34)

すなわちσ²は12の互換と34の互換の作用素となっています。また

• σ³(x、－x、ix、－ix)＝σ²(ix、－ix、－x、x)＝σ(－x、x、－ix、ix)

＝(－ix、ix、x、－x)＝(α₄,α₃,α₁,α₂)

　　σ³＝(1→4→2→3→1)＝(1423)

すなわちσ³は(1423)の置換作用素となっています。τに関しても

• τ(x、－x、ix、－ix)＝(x、－x、－ix、ix)＝(α₁,α₂,α₄,α₃) ＝(34)

すなわちτは34の互換のみの作用素です。

• τσ(x、－x、ix、－ix)＝τ(ix、－ix、－x、x) ＝(－ix、ix、－x、x)＝(α₄,α₃,α₂,α₁)

　　τ＝(1→4→1、2→3→2)＝(14)(23)

すなわちτσは14の互換と23の互換の作用素となっています。

• τσ²(x、－x、ix、－ix)＝τ(－x、x、－ix、ix)＝(－x、x、ix、－ix)＝(α₂,α₁,α₃,α₄)

　　τσ²＝(12)　となっています。

• τσ³(x、－x、ix、－ix)＝τ(－ix、ix、x、－x)＝(ix、－ix、x、－x)＝(α₃,α₄,α₁,α₂)

　　τσ³＝(1→3→1、2→4→2)＝(13)(24) となっています。

＜まとめ＞

多項式f(x)＝x⁴－3の分解体とガロア群を求め、拡大体の系列と対応するガロア群の系列を7種類導出しました。f(x)の分解体はQ(⁴√3,i)であり、その上の有理数体を不変に保つQ自己同型写像全体は8次のD₄群となることを、群の演算表を作成して示しました。D₄の部分群には3つの4次の部分群と5つの2次の部分群がありました。部分群の作用で不変となる不変体を求めました。ガロア群に対応する不変体は拡大体の系列を構成することを示しました。

(1) D₄⊃K₄⊃S₂⊃I　⇔　Q⊂Q(i)⊂Q(√3,i)⊂Q(⁴√3,i)

(2) D₄⊃L₄⊃S₂⊃I  ⇔  Q⊂Q(√3)⊂Q(√3,i)⊂Q(⁴√3,i)

(3) D₄⊃L₄⊃T₂⊃I  ⇔ Q⊂Q(√3)⊂Q(⁴√3)⊂Q(⁴√3,i)

(4) D₄⊃L₄⊃V₂⊃I  ⇔ Q⊂Q(√3)⊂Q(⁴√3i)⊂Q(⁴√3,i)

(5) D₄⊃M₄⊃S₂⊃I  ⇔ Q⊂Q(√3i)⊂Q(√3,i)⊂Q(⁴√3,i)

(6) D₄⊃M₄⊃U₂⊃I  ⇔ Q⊂Q(√3i)⊂Q((1－i)-⁴√3)⊂Q(⁴√3,i)

(7) D₄⊃M₄⊃W₂⊃I  ⇔ Q⊂Q(√3i)⊂Q((1＋i)-⁴√3)⊂Q(⁴√3,i)