リ－マンのゼータ関数ζ(s)は、

• ζ(s)＝Σ_{[n＝1～∞]} 1／n^s＝1＋1／2^s＋1／3^s＋・・・

Re(s)＞1で収束します。これをζ(s)のディリクレ級数表示ともいいます。

ｓ＞1ならば、2≦n≦Nに対して、n－1＜x＜nの時、

• 　1/n^s＜1/x^s＜1/(n－1)^s

が成り立つので、

• 1/n^s＜∫_[n－1,n]1/x^s dx ＜1/(n－1)^s
• Σ_[n=2～N] 1/n^s＜Σ_[n=2～N]∫_[n－1,n]1/x^s dx ＜Σ_[n=2～N] 1/(n－1)^s
• Σ_[n=2～N] 1/n^s＜∫_[1,N]1/x^s dx ＜Σ_[n=2～N] 1/(n－1)^s
• Σ_[n=1～N] 1/n^s－1＜∫_[1,N]1/x^s dx ＜Σ_{[n=1～N－1]} 1/n^s

ここで

• ∫_[1,N]1/x^s dx＝[x^1－S/(1－s)]x＝1,N　＝1/(s‐1)[1－N^1－s]＜1/(s‐1)

なので、

• Σ_[n=1～N] 1/n^s＜1＋1/(s‐1)　→　Σ_[n=1～∞] 1/n^sは収束する

従って

• 1/(s‐1) ≦ζ(s) ≦1＋1/(s‐1)　for s＞1

より、

• Lim_[s→+1] ζ(s)＝∞　かつ　Lim_[s→+1] (s‐1)ζ(s)＝1

が得られます。

 

s＝1のときは、ζ(s)は調和級数となり

• Σ_{[n＝1～∞]} 1／n＝1＋1／2＋1／3＋・・・＝log(∞)

対数発散をします。これは積分判定法から分かります。

積分判定法とは、正の単調減少関数f(x)によって、数列a_nを、a_n＝f(n)と定義すると、

• Σ_[n=1～∞] a_nが収束　⇔　∫_[1,∞] f(x) dxが収束

が成り立つというものです。よって

• ∫_[1,∞] 1/x dx＝log(∞)　→　Σ_{[n＝1～∞]} 1／n＝log(∞)

だと分かります。あるいは任意の正の整数ｋに対して

• Σ_[n=1～2k]1/n ＞ 1＋k/2　→　as k →∞

により示すことができます。

 

ゼータ関数ζ(s)のオイラ－積表示は

• ζ(s)＝Π_[p] [1/(1‐1/p^s)]

はディリクレ級数表示と一致するでしょうか。

s＞1のとき、有限積

• P_N(s)＝Π_[p≦N] [1/(1‐1/p^s)]

を考えます。

• 1/(1‐1/p^s)＝Σ_[k=0～∞] (p^－s)^k＝1＋1/p^s＋1/p^2s＋1/p^3s＋・・・

を代入して、P_N(s)を展開すると、素因数分解の一意性より

• Σ_[n＝1～N] 1/n^s ＜ P_N(s)＝Σ[nの各素因数≦N] 1/n^s ＜Σ_{[n＝1～∞]} 1/n^s＝ζ(s)

が成り立つので、

• Π_[p] [1/(1‐1/p^s)]＝Lim_[N→∞] P_N(s)＝ζ(s)

ゼータ関数ζ(s)はオイラ－積表示可能であることが示されました。

 

ゼータ関数ζ(s)は、s＞0（s≠1）に拡張することができます。

• ζ(s)＝L(s)／(1－2^1－s)　、L(s)＝Σ_{[n＝1～∞]}(－1)^(n－1)/n^s

右辺はs＞0（s≠1）で収束します。実際部分和L_N(s)＝Σ_[n＝1～N](－1)^(n－1)/n^sを考えると、

• 0＜1－1/2^s＝L₂＜L₄＜・・・＜L_2N＜L_2N+2＜L_2N+1＜L_2N－1＜・・・＜L₃＜L₁＝1

偶数番目の部分和L_2nは上に有界で単調増加、奇数番目の部分和L_2n-1は下に有界で単調減少なので、それぞれ収束し、s＞0のとき

• L_2N－L_2N-1＝－1/(2N)^s　→ 0 　as 　N →∞

だから、

• Lim_[N→∞] L_2N＝Lim_[N→∞]L_2N-1＝L(s)

となります。

• ζ(s)‐L(s)＝2Σ_{[n＝1～∞]}1/(2n)^s＝2^(1－s)・Σ_{[n＝1～∞]}1/n^s＝2^(1－s) ζ(s)

よって、

• ζ(s)＝L(s)／(1－2^1－s)　for　s＞0（s≠1）

が示されました。s＞0のときは、ζ(s)はL(s)/(1－2^1－s)だと再定義します。

0＜s＜1のとき、L(s)＞0で(1－2^1－s)＜0なので、ζ(s)＜0であり、

• Lim_[s→1-δ] ζ(s)＝－∞

となります。正の関数を解析接続すると負の関数になるのは驚きです。

実はガンマ関数を用いると、s＜0の領域にもζ(s)を拡張することができます。

結果だけ書くと、

• ζ(s)＝2^sπ^s‐1・sin(πs/2)・Γ(1－s)・ζ(1－s)　 s＜0（s≠1）

右辺は1－s＞1で定義されるので、左辺はｓ＜0で定義できます。

• sin(πs/2)＝0　for　s＝－2、－4、－6、・・・

なので、

• ζ(－2k)＝0　（kは正の自然数）

となります。これらの負の零点をゼータ関数の自明な零点といいます。

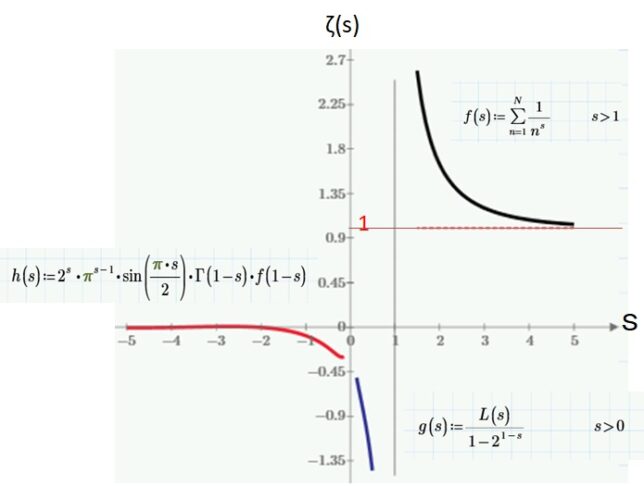
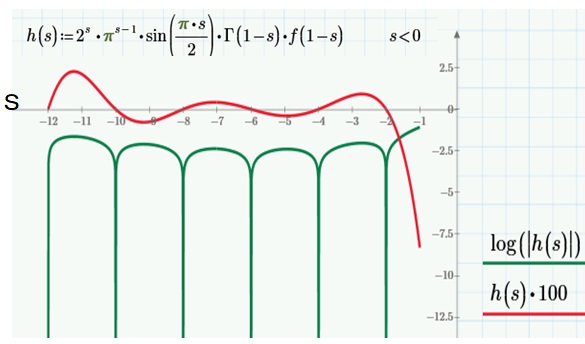
下図にゼータ関数の外形を示します。N＝10000までの和で計算表示しました。本来、赤線と青線はｓ＝0でｙ＝－1/2で接続します。ｓ＜0の部分は、振動しており、負の偶数は零点になっています。