数学というのは登山とよく似ています。知らない山に登るのは大変ですが、その分登頂の絶景には感動します。景色を忘れてしまっても、登頂の達成感は長く心に残ります。数学も同じように、知らない定理を理解するのは大変ですが、その分定理の威力に感動します。もしその定理を忘れてしまっても、理解した達成感は長く心に残ります。登山が遊びなら、数学も遊びなのです。

これまで高次方程式の解を求め、解を表示する拡大体とその上の自己同型群との対応関係を調べてきました。今日はガロアの基本定理を証明します。ガロアの定理は部分群Hが対応する拡大体Bを不変にするとき、拡大体Bは対応する部分群Hの不変体になっており、両者に対応関係があることを示しています。ガロアの定理に従って方程式の解を引き受ける拡大体上の同型写像の群を分解して解析すると、元の方程式が代数的に解けるのかどうかを確かめることができます。

そのための準備として、2つの定理を紹介します。最初の定理はアルティンの定理です。それは『体E上のn個の相異なる同型写像による不変体KからEへの体の拡大次数はn以上である』という主張です。2番目の定理は『先ほどの同型写像が群であれば、拡大次数はちょうど群の要素数に一致する』というものです。これらの定理からガロアの基本定理が証明されます。

 

＜アルティンの定理1＞

体Eから体Fへのn個の相異なる同型写像σ₁、σ₂、・・・σ_nがあるとする。これらの同型写像による不変体KからEへの体の拡大次数はn以上である。

 

同型写像　σ₁、σ₂、・・・σ_n；E　→　F

不変体　K＝｛x∊E｜σ₁(x)＝σ₂(x)＝・・・＝σ_n(x)｝

→　KからEへの体の拡大次数　[E：K]≧n

 

証明）σ₁、σ₂、・・・σ_nが体Eから体Fへのn個の相異なる同型写像であれば、

σ₁、σ₂、・・・σ_nは線形独立です。まずこの事実を証明しましょう。

例えば、n＝2のとき、σ₁≠σ₂より∃α∊E、σ₁(α)≠σ₂(α)。

　x₁σ₁＋x₂σ₂＝0　ならば、任意のx∊Eに対して、x₁σ₁(x)＋x₂σ₂(x)＝0。σ₁(α)を掛け、

   x₁σ₁(α)σ₁(x)＋x₂σ₁(α)σ₂(x)＝0

が成り立ちます。またαx∊Eに対して、x₁σ₁(αx)＋x₂σ₂(αx)＝0。つまり

   x₁σ₁(α)σ₁(x)＋x₂σ₂(α)σ₂(x)＝0

が成り立ちます。上の2式を引き算すると、任意のx∊Eに対して

    (σ₁(α) －σ₂(α))・x₂σ₂(x)＝0。

σ₁(α)≠σ₂(α)なので、x₂＝0となります。代入してx₁＝0も得られます。

   x₁σ₁＋x₂σ₂＝0　ならば、x₁＝x₂＝0

が示されたので、σ₁、σ₂は線形独立です。n＝3の場合も同様にして

　x₁σ₁＋x₂σ₂＋x₃σ₃＝0　ならば、x₁＝x₂＝x₃＝0

が成り立ちます。実際

　x₁σ₁(α)σ₁(x)＋x₂σ₁(α)σ₂(x) ＋x₃σ₁(α)σ₃(x)＝0

　x₁σ₁(α)σ₁(x)＋x₂σ₂(α)σ₂(x) ＋x₃σ₃(α)σ₃(x)＝0

両式を引き算すると、任意のx∊Eに対して、

　(σ₁(α) －σ₂(α))・x₂σ₂(x)＋(σ₁(α) －σ₃(α))・x₃σ₃(x)＝0。

σ₁(α)≠σ₂(α) 、σ₁(α)≠σ₃(α)であり、2つの元σ₂とσ₃は線形独立なので、x₂＝x₃＝0となります。x₂＝x₃＝0を代入して

　x₁σ₁(α)σ₁(x)＝0。

よってx₁＝0も得られます。このようにして、σの元の数をnまで増やすことができます。

次に[E：K]＝r ＜n と仮定すると矛盾が生じることを示します。これは体K上のベクトル空間Eに｛α₁、α₂、・・・α_r｝のr個の基底が存在することを示しています。以下の連立方程式は、

　  σ₁(α₁)x₁＋σ₂(α₁)x₂＋σ₃(α₁)x₃＋・・・＋σ_n(α₁)x_n＝0

      σ₁(α₂)x₁＋σ₂(α₂)x₂＋σ₃(α₂)x₃＋・・・＋σ_n(α₂)x_n＝0

　　・・・・・・・

      σ₁(α_r)x₁＋σ₂(α_r)x₂＋σ₃(α_r)x₃＋・・・＋σ_n(α_r)x_n＝0

方程式の数rが未知数x₁,x₂…,x_nの数nより小さいので自明でない解x₁,x₂…,x_nを持ちます。[E：K]＝rより、体K上のベクトル空間Eの任意の元α∊Eはa_1、a_{2、・・・}a_r ∊Kを用いて

     α＝a₁α₁+a₂α₂+・・・+ a_rα_r

と書けます。上記の方程式にσ₁(a₁)を掛けると

     σ₁(a₁)σ₁(α₁)x₁＋σ₁(a₁)σ₂(α₁)x₂＋・・・＋σ₁(a₁)σ_n(α₁)x_n＝0。

Kは同型写像の不変体だから、

      σ₁(a₁)＝σ₂(a₁) ＝σ₃(a₁) ＝…＝σ_ｎ(a₁)

が成り立つことを利用すると、上式は

       σ₁(a₁)σ₁(α₁)x₁＋σ₂(a₁)σ₂(α₁)x₂＋・・・＋σ_n(a₁)σ_n(α₁)x_n＝0

となります。同型写像ですから

       σ₁(a₁α₁)x₁＋σ₂(a₁α₁)x₂＋σ₃(a₁α₁)x₃・・・＋σ_n(a₁α₁)x_n＝0

が成り立ちます。他の方程式も同様に変形すると

　  σ₁(a₁α₁)x₁＋σ₂(a₁α₁)x₂＋σ₃(a₁α₁)x₃・・・＋σ_n(a₁α₁)x_n＝0

      σ₁(a₂α₂)x₁＋σ₂(a₂α₂)x₂＋σ₃(a₂α₂)x₃・・・＋σ_n(a₂α₂)x_n＝0

      ・・・・・・

       σ₁(a_rα_r)x₁＋σ₂(a_rα_r)x₂＋σ₃(a_rα_r)x₃・・・＋σ_n(a_rα_r)x_n＝0

を得ます。これらの方程式を辺々加えます。第一項の和は

      σ₁(a₁α₁)x₁＋σ₁(a₂α₂)x₁＋・・・＋σ₁(a_rα_r)x₁

   ＝{σ₁(a₁α₁)＋σ₁(a₂α₂)＋・・・＋σ₁(a_rα_r)}x₁

   ＝σ₁(a₁α₁＋a₂α₂＋・・・＋a₂α_r)x₁

   ＝σ₁(α)x₁

となるので、任意の元α∊Eに対して

     σ₁(α)x₁＋σ₂(α)x₂＋σ₃(α)x₃＋・・・＋σ_n(α)x_n＝0

が成り立ちます。σ₁、σ₂、・・・σ_nは相異なる同型写像で、σ_i(α)≠0です。またx₁,x₂…, x_nの中には0でないものが必ず一つはあります。よってσ₁、σ₂、・・・σ_nは線形独立ではありません。これはσ₁、σ₂、・・・σ_nが線形独立であることと矛盾します。つまり[E：K]＝r ＜n という仮定が誤っていたことを示しています。よって    [E：K]≧n  が示されました。証明終わり。

アルティンの定理では｛σ₁、σ₂、・・・σ_n｝が群を成すと仮定していません。実際｛σ₁、σ₂、・・・σ_n｝が群を成さないのであれば、あるσ_i^-1、かσ_iσ_jが｛σ₁、σ₂、・・・σ_n｝以外の元になります。x∊Kに対して、 (σ_iσ_j) (x)＝σ_i(σ_j (x))＝σ_i(x)＝xとなり、不変体 K＝｛x∊E｜σ₁(x)＝σ₂(x)＝・・・＝σ_n(x)＝σ_iσ_j(x)＝x ｝を構成する相異なる自己同型写像｛σ₁、σ₂、・・・σ_n、σ_iσ_j｝はn+1個になります。あるいは、x＝e(x)＝(σ_i^-1σ_i) (x)＝σ_i^-1(σ_i(x) )＝σ_i^-1(x )となり、不変体 K＝｛x∊E｜σ₁(x)＝σ₂(x)＝・・・＝σ_n(x)＝σ_i^-1(x)＝x｝を構成する相異なる自己同型写像｛σ₁、σ₂、・・σ_n、σ_i^-1｝はn+1個になります。よって[E：K]≧n+1 となります。不変体 Kを構成する自己同型写像｛σ₁、σ₂、・・・σ_n｝が群をなしていれば、演算で新しい元は生成しません。不変体 Kを構成する自己同型写像はn個に限られるので[E：K]＝nとなります。それを保証するのが次の定理です。

定理2

体E上のn個の相異なる自己同型写像σ₁、σ₂、・・・σ_nが群Gをなす場合、群Gの不変体Kから体Eへの拡大次数はnとなる。

自己同型写像　σ₁、σ₂、・・・σ_n；E　→　E

群G＝｛σ₁、σ₂、・・・σ_n｝

不変体 K＝｛x∊E｜σ₁(x)＝σ₂(x)＝・・・＝σ_n(x)｝

→　KからEへの体の拡大次数　[E：K]＝n

注意）標数0の体に限定する。標数nとは、n・1＝0を満たす数。複素数体は標数0。

証明）[E：K]≦nを示せれば、前定理[E：K]≧nと合わせて、[E：K]＝nとなります。

任意のx∊Eに対して、トレ－ス

     S(x)＝σ₁(x)＋σ₂(x)＋・・・σ_n(x) ∊E

を定義します。｛σ₁、σ₂、・・・σ_n｝は群を成しているので、任意のi＝1,2、…nに対して、

      σ_i・｛σ₁、σ₂、・・・σ_n｝＝｛σ₁、σ₂、・・・σ_n｝

です。従って

　σ_i(S(x))＝σ_iσ₁(x)＋σ_iσ₂(x)＋・・・σ_iσ_n(x)＝σ₁(x)＋σ₂(x)＋・・・σ_n(x)＝S(x)

であるから、S(x) ∊Kとなります。K係数のベクトル空間Eの次元がｎ以下であることを示すために、ベクトル空間Eのn+1個の基底｛α₁,α₂,…α_n,α_n+1｝が一次独立ではないことを示せばよいです。Gは群であるために、σ_i^-1∊Gが存在します。連立方程式

　σ₁^-1(α₁) x₁＋σ₁^-1(α₂) x₂＋・・・＋σ₁^-1(α_n) x_n＋σ₁^-1(α_n+1) x_n+1＝0

    σ₂^-1(α₁) x₁＋σ₂^-1(α₂) x₂＋・・・＋σ₂^-1(α_n) x_n＋σ₂^-1(α_n+1) x_n+1＝0

　  ・・・・・・・・・・・・・・

     σ_n^-1(α₁) x₁＋σ_n^-1(α₂) x₂＋・・・＋σ_n^-1(α_n) x_n＋σ_n^-1(α_n+1) x_n+1＝0

に関して、未知数x₁,x₂…,x_n+1の個数ｎ＋1は式の個数ｎより大きいので、x₁,x₂…,x_n+1はx₁＝x₂＝…＝x_n+1＝0の自明な解以外の少なくとも一つはゼロではない非自明解を持ちます。非自明解をx₁≠0とすると、x₁≠0で全体を割ることで、x₁＝1として良いです。i番目の方程式にσ_iを作用させると、

       σ_i (σ_i^-1(α₁) x₁) ＋σ_i (σ_i^-1(α₂) x₂)＋・・・＋σ_i(σ_i^-1(α_n+1) x_n+1)＝0

　　α_1・σ_i(x₁)＋α_2・σ_i(x₂) ＋・・・＋α_n+1・σ_i (x _n+1) ＝0

となります。これをすべての方程式について行うと

        α_1・σ₁(x₁)＋α_2・σ₁(x₂) ＋・・・＋α_n+1・σ₁(x _n+1) ＝0

        α_1・σ₂(x₁)＋α_2・σ₂(x₂) ＋・・・＋α_n+1・σ₂(x _n+1) ＝0

　　　・・・・・・・・・・・・・・　

　     α_1・σ_n(x₁)＋α_2・σ_n(x₂) ＋・・・＋α_n+1・σ_n(x _n+1) ＝0

を得ます。辺々を加えると、S(x)＝σ₁(x)＋σ₂(x)＋・・・σ_n(x) ∊Kを用いると

         S(x₁)α₁＋S(x₂)α₂ ＋・・・＋S(x _n+1)α_n+1＝0

S(x_i)∊K、つまりS(x₁)、S(x₂)、・・・S(x _n+1)はK係数であります。

｛α₁,α₂,…α_n,α_n+1｝が一次独立ならば、S(x₁)＝S(x₂)＝・・・＝S(x _n+1)＝0

です。しかし

      S(x₁)＝S(1)＝σ₁(1)＋σ₂(1)＋・・・＋σ_n(1)＝1+1+・・・+1＝n≠0

ので、ベクトル空間Eのn+1個の基底｛α₁,α₂,…α_n,α_n+1｝が一次独立ではないことが示されました。ベクトル空間Eの次元はn次元以下 [E：K]≦nが示されました。前定理[E：K]≧nと合わせて、拡大体の次数は[E：K]＝nとなります。証明終わり。

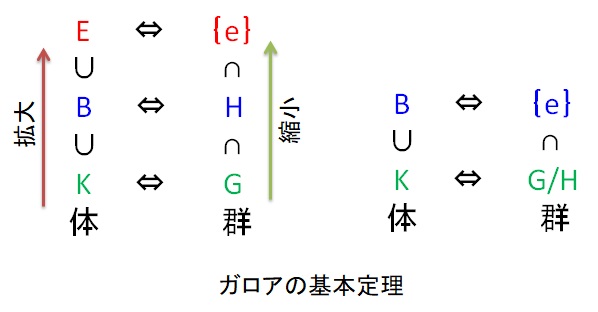
＜ガロアの基本定理＞

[1]EをKの正規拡大体、そのK自己同型群Aut_K(E)をGとする。E⊃B⊃Kなる中間体Bを不変にするGの部分群H＝｛σ∊G｜∀x∊B、σ(x)＝x｝があれば、

(1)EはBの正規拡大体である。

(2)HがBのK自己同型群である。

(3)中間体Bと群Hは一対一に対応する。

[2] HがGの正規部分群であれば、

(1)BはKの正規拡大体である。

(2) G/HがBのK自己同型群である。

(3)体Kと余剰群G/H一対一に対応する。

注意1）x∊Bにおいて、任意のσ₁,σ₂∊Hに対して、σ₁σ₂(x)＝σ₁(σ₂(x))＝σ₁(x)＝xより、σ₁σ₂∊H。またσ₁(x)＝xよりx＝σ₁^-1σ₁ (x)＝σ₁^-1 (x)なので、σ₁^-1∊Hとなります。よってHの定義からHはすでに群になっています。

注意2）EはBの正規拡大体であるとは、BがE上の自己同型写像の作る群Hの不変体になっていることです。このとき[E；B]＝＃(H)が成り立ちます。

注意3）Hが正規部分群であれば、G/Hは群になります。Hが正規部分群でなければ、G/Hは群になりません。

[1] (1) EはBの正規拡大体であることの証明）

Hの要素数を＃(H)＝rとすると、群H＝｛σ∊G｜∀x∊B、σ(x)＝x｝の定義から∀x∊Bに対して、σ₁,σ₂,…σ_r ∊H⊂G、σ₁(x)＝σ₂(x)＝…＝σ_r(x)＝xが成り立つので、定理2より[E；B]＝rが成り立ちます。次にBはHの不変体であることを示します。Hの不変体をB’＝｛x∊E｜∀σ∊H、σ(x)＝x｝とします。Bの定義から∀x∊Bに対して、∀σ∊H、σ(x)＝xなので、B’の定義からx∊B’が成り立ちます。よってB’⊃Bです。Hは群であり、B’はHの不変体なので、定理2より[E；B’]＝rが成り立ちます。[E；B]＝[E；B’]かつB’⊃Bより、B＝B’となります。つまりBがE上の自己同型写像の作る群Hの不変体になっており、[E；B]＝＃(H)が成り立つので、EはBの正規拡大体であることが示されます。証明終わり。

[1] (2) HがBのK自己同型群であることの証明）

＃(G/H)＝sとすると、ラグランジュの定理より、N＝＃(G)＝＃(H) -＃(G/H)＝r・sです。σ、σ’∊Gが同じ剰余類G/Hに属するとすると、σ^-1σ’ ∊Hとなります。H＝｛σ∊G｜∀x∊B、σ(x)＝x｝の定義より、∀x∊Bに対して、σ^-1σ’(x)＝x、すなわちσ’(x)＝σ(x)です。つまり同じ剰余類G/Hに属するσはB上で同じ同型写像を与えます。σ∊GはE上のK自己同型写像ですが、これをB上に限定すると、＃(G/H)＝sより、BからEへの相異なるs個のK同型写像が存在します。

[1] (3) 中間体Bと群Hは一対一に対応することの証明）

Hが正規部分群でなければ、G/Hは群にならないので、アルティンの定理より[B：K]≧sとなります。n＝[E：K] ＝[E：B] [B：K] ≧rs＝n、[B：K]≧sより[B：K]＝sとなります。つまりBの基底s個とB上の同型写像の個数s∊G/Hは対応しています。群Gを中間体Bで制限した群G^B＝｛σ∊G｜∀x∊B⊂E、σ(x)＝x｝をHとすることで、中間体Bが体Eを部分群Hで制限した体E^H＝｛x∊E｜∀σ∊H⊂G、σ(x)＝x｝となるので、中間体Bと部分群Hは一対一に対応します。

・HがGの正規部分群であるとき、

[2] (1)BはKの正規拡大体であることの証明）

BはKの正規拡大体であるとは、KがB上の自己同型写像の作る群G/Hの不変体になっていることです。σがB上の自己同型写像であるとは、σ(B)＝Bということです。このとき[B；K]＝＃(G/H)が成り立ちます。H＝｛σ∊G｜∀x∊B、σ(x)＝x｝と定義されています。E上の自己同型写像σ∊Gに対して、σ(B)⊂Eです。中間体σ(B)を不変にする群はσHσ^-1になっています。なぜならば、τ∊σHσ^-1⇔　σ^-1τσ∊H　であることはHの定義により任意のx∊Bにおいて、σ^-1τσ(x)＝x　　⇔　τσ(x)＝σ(x)　すなわちτ(σ(B))＝σ(B)を意味するからです。Hが正規群であれば、任意のσ∊Gに対して、σHσ^-1＝Hです。今Hが正規群なので、τ∊Hに対してτ(σ(B))＝σ(B)、すなわちσ(B)はHの不変体になっています。先ほどHの不変体はBであることを証明したので、σ(B)＝B⊂Eが示されました。中間体Bは群G/H＝σHσ^-1の不変体になっているので、BはKの正規拡大体です。逆に任意のσ∊Gに対して、σ(B)＝Bならば、τ∊σHσ^-1に対してτ(B)＝Bとなります。これはσHσ^-1＝HすなわちHはGの正規部分群であることを意味します。

[2] (2) G/HがBのK自己同型群であることの証明）

任意のx∊Bにおいて、σ(x)＝σ’(x)　⇔　σ’^-1σ(x)＝xとなり、σ’^-1σ∊Hとなります。これはσ’、σが同じG/Hの類に属していることを意味するので、Aut_K(B)＝G/Hです。証明終わり。

前回はf(x)＝x³－2を例に、f(x)の分解体とガロア群を求めました。今回は多項式の次数を1つ上げて、拡大体の列と対応するガロア群の列を導出します。

Ex.3　　Q多項式f(x)＝x⁴－3を例に、f(x)の分解体とガロア群を求めてみましょう。

f(x)を因数分解すると

• f(x)＝x⁴－3＝(x²－⁴√9) ( x²＋⁴√9)＝(x－⁴√3) ( x＋⁴√3) ( x－⁴√3i) ( x＋⁴√3i)、
• i²＝－1、i³＝－i、i⁴＝1

となります。f(x)＝0の4つの解は、

• α₁＝⁴√3、α₂＝－⁴√3、α₃＝⁴√3i、α₃＝－⁴√3i

となります。f(x)の分解体は4つの解をQに付け加えたものですが、⁴√3とiの2つを付け加えることに等しいので、f(x)の分解体はQ(⁴√3,i)となります。⁴√3をべき乗してゆくと、

1． ⁴√3、⁴√9、⁴√27の4つの基底が得られます。a_0、a_{1、・・・}a₇ ∊Q（有理数）を用いて、

・　Q(⁴√3、i)＝｛a₀＋a_1・⁴√3＋a_2・⁴√9＋a_3・⁴√27＋a₄i＋a_5・⁴√3i＋a_6・⁴√9i ＋a_7・⁴√27i｝

と書けます。体の拡大の次数は8となります。

• [Q(⁴√3、i)：Q]＝[Q(⁴√3、i)：Q(⁴√3)]・[Q(⁴√3)：Q]＝2・4＝8

拡大体Q(⁴√3、i)上のQ自己同型写像σ∊Aut_Q(Q(⁴√3、i))を求めます。σは同型なので

• σ(ab)＝σ(a)・σ(b)、σ(a＋b)＝σ(a)＋σ(b)　for a,b∊Q

を満たします。またσは3∊Qを不変に保つので

• 3＝σ(3)＝σ( (⁴√3)⁴) ＝σ(⁴√3) ⁴

となります。σを⁴√3にiを掛ける作用とiを不変にする作用を持つ写像

• σ(⁴√3)＝⁴√3i、σ(i)＝i

だとすると、上式を満たす4つの写像は、

σ(⁴√3)＝⁴√3i、σ²(⁴√3)＝⁴√3ii＝－⁴√3、σ³(⁴√3)＝⁴√3iii＝－⁴√3i、σ⁴(⁴√3)＝⁴√3

と表現できます。σ⁴は恒等写像です。また―1∊Qを不変に保つ写像をτとすると

• －1＝τ(－1)＝τ(ii)＝τ(i)²

なので、τはiに－1を掛ける作用と⁴√3を不変にする作用を持つ写像

• τ(i)＝－i、τ(⁴√3)＝⁴√3

だとします。τ²(i)＝iなのでτ²は恒等写像です。Q(⁴√3、i)/Q上のガロア群Gは

• G＝Gal(Q(⁴√3、i)/Q)＝｛e、σ、σ²、σ³、τ、στ、σ²τ、σ³τ｝、＃(G)＝8

となります。Gの位数は8となり、体の拡大の次数8と一致します。これらの写像は

• τσ²(⁴√3)＝τ(－⁴√3)＝－⁴√3、σ²τ(⁴√3)＝σ²(⁴√3)＝－⁴√3
• στσ(⁴√3)＝στ(⁴√3i)＝σ(－⁴√3i) ＝－⁴√3ii＝⁴√3＝τ(⁴√3)
• τστ(⁴√3)＝τσ(⁴√3) ＝τ(⁴√3i)＝－⁴√3i、σ³(⁴√3)＝⁴√3iii＝－⁴√3i

であるから、

• τσ²＝σ²τ　⇔　σ^－2(σ²τ) σ^－2＝σ²τ
• στσ＝τ、τ^－1＝τ、τστ＝σ³　⇔　(τσ)^－1＝τσ

なる性質があります。これらから

• στ・σ²τ＝στ・τσ²＝σ³
• στ・σ³τ＝στσ・σ²τ＝τσ²τ＝σ²
• τ・σ²τ＝τσ²・τ＝σ²τ・τ＝σ²
• τ・σ³τ＝τσ²・στ＝σ²τ・στ＝σ²・τστ＝σ²・σ³＝σ・σ⁴＝σ
• σ³τ・σ³τ＝σ³・σ＝e
• σ²τ・σ³τ＝σ²・σ＝σ³
• σ²τ・σ²τ＝σ²τ・τσ²＝σ
• σ²・τ＝σ・ττ・στ＝στσ³＝ττστσ³＝τσ³σ³＝τσ²
• σ²・τσ＝σ・στσ＝στ＝τστ＝τσ³
• σ²・τσ²＝τσ³σ＝τ
• σ³・τ＝στσ²＝τσ
• σ³・τσ＝τσ²

が成り立ちます。8つの元同士の演算の結果を次の演算表にまとめました。

ここで

• τ（縦の元）・σ（横の元）＝τσ（表中の元）
• σ（縦の元）・τ（横の元）＝τσ³（表中の元）

に注意して下さい。τσⁿの逆元はτσⁿになっていることが分かります。8個の元同士の演算が8個の元で閉じているので、Gは群になっています。これはD₄と呼ばれ、四角板の1/4回転と反転操作のなす群に相当します。

f(x)の分解体Q(⁴√3,i)上のQ自己同型写像全体は8次のD₄群となりました。

• D₄＝｛e、σ、σ²、σ³、τ、τσ、τσ²、τσ³｝

Q自己同型写像というのは、有理数体Qは不変に保つQ(⁴√3,i)からQ(⁴√3,i)への全単射写像という意味です。次にD₄の部分群を調べます。4次の部分群はK₄、L₄、M₄の3つがあります。

• K₄＝｛e、σ、σ²、σ³｝＝Z/4Z
• L₄＝｛e、σ²、τ、τσ²｝＝Z/2Z×Z/2Z
• M₄＝｛e、σ²、τσ、τσ³｝＝Z/2Z×Z/2Z

2次の部分群はS₂、T₂、U₂、V₂、W₂の5つがあります。

・　S₂＝｛e、σ²｝、T₂＝｛e、τ｝、U₂＝｛e、τσ｝、V₂＝｛e、τσ²｝、W₂＝｛e、τσ³｝

｛e、τσ^k｝（k＝0,1,2,3）は4つの2次の部分群を作ります。自明な1次の部分群

・　I＝{e}

があります。

ガロア群の包含関係は7種類あります。7種類の群の系列に対応する拡大体の系列を示します。

• D₄⊃K₄⊃S₂⊃I　　

         Q⊂Q(i)⊂Q(√3,i)⊂Q(⁴√3,i)

• D₄⊃L₄⊃S₂⊃I

         Q⊂Q(√3)⊂Q(√3,i)⊂Q(⁴√3,i)

• D₄⊃L₄⊃T₂⊃I

         Q⊂Q(√3)⊂Q(⁴√3)⊂Q(⁴√3,i)

• D₄⊃L₄⊃V₂⊃I

         Q⊂Q(√3)⊂Q(⁴√3i)⊂Q(⁴√3,i)

• D₄⊃M₄⊃S₂⊃I

         Q⊂Q(√3i)⊂Q(√3,i)⊂Q(⁴√3,i)

• D₄⊃M₄⊃U₂⊃I

         Q⊂Q(√3i)⊂Q((1－i)-⁴√3)⊂Q(⁴√3,i)

• D₄⊃M₄⊃W₂⊃I

         Q⊂Q(√3i)⊂Q((1＋i)-⁴√3)⊂Q(⁴√3,i)

[1]　K₄＝Gal(Q(i)/Q)を示します。a₀,a_1、、、a₇∊Qに対して、x=⁴√3とおきます。                   _、

X＝a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ ∊Q(x,i)

σ∊K₄に対して、σ(X)＝Xとなる係数の条件を求めます。σ(x)＝ix、σ(i)＝iです。

　σ(a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ )

＝a₀+ a₁xi－a₂x²－a₃ix³+ a₄i－a₅x－a₆ix²+ a₇ x³

• a₁＝－a₅、a₂＝－a₂＝0、a₃＝a₇、a₅＝a₁、a₆＝－a₆＝0、a₇＝－a₃、

→　a₁＝a₂＝a₃＝a₅＝a₆＝a₇＝0

　　X＝a₀+ a₄i∊Q(i)

K₄＝｛e、σ、σ²、σ³｝の全ての元に対して、σ(X)＝Xが成り立つので、K₄は拡大体Q(i)/Q上のガロア群になっています。Q(i)はK₄の不変体になっています。

D₄⊃K₄⊃S₂⊃I　　⇔　　Q⊂Q(i)⊂Q(√3,i)⊂Q(⁴√3,i)

• S₂＝｛e、σ²｝＝Gal(Q(√3、i)/Q)を示します。
• σ²(a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ )

＝σ(a₀+ a₁xi－a₂x²－a₃ix³+ a₄i－a₅x－a₆ix²+ a₇ x³)

　　＝a₀－a₁x＋a₂x²－a₃x³+ a₄i－a₅ix＋a₆ix²－a₇ix³

　　a₁＝－a₁、a₃＝－a₃＝0、a₅＝－a₅、a₇＝－a₇、→　a₁＝a₃＝a₅＝a₇＝0

　　X＝a₀＋a₂x² + a₄i＋a₆ix²＝a₀＋a₂√3 + a₄i＋a₆√3 i　∊Q(√3、i)

S₂＝｛e、σ²｝の全ての元に対して、σ²(X)＝Xが成り立つので、S₂は拡大体Q(√3、i)上のガロア群になっています。K₄はD₄の正規部分群、S₂はK₄の正規部分群になっています。

Q(√3、i)は、｛1、√3、i、√3i｝の4つの基底からなる4次元ベクトル空間と同型です。

Q(i)は、｛1、i｝の2つの基底からなる2次元ベクトル空間と同型です。

• D₄⊃K₄⊃S₂⊃I　　⇔　Q⊂Q(i)⊂Q(√3,i)⊂Q(⁴√3,i)
• [Q(⁴√3、i)：Q]＝[Q(⁴√3、i)：Q(√3、i)]・[Q(√3、i)：Q(i)]・[Q(i)：Q]＝2・2・2＝8
• ＃(D₄)＝＃(K₄)・＃(S₂)・＃(I)＝4・2・1＝8

[2] L₄＝｛e、σ²、τ、τσ²｝＝Gal(Q(√3)/Q)を示します。τ(i)＝－i

σ²(X)＝Xより、X＝a₀＋a₂x² + a₄i＋a₆ix²

τ(X)＝τ(a₀＋a₂x² + a₄i＋a₆ix²)＝a₀＋a₂x² －a₄i－a₆ix²＝a₀＋a₂x² + a₄i＋a₆ix²

• －a₄＝a₄＝0、－a₆＝a₆＝0　→　X＝a₀＋a₂x² ＝a₀＋a₂√3　∊Q(√3)

従ってQ(√3)はL₄の不変体になっており、以下のガロア対応が成り立ちます。

• D₄⊃L₄⊃S₂⊃I　⇔　Q⊂Q(√3)⊂Q(√3,i)⊂Q(⁴√3,i)
• [Q(⁴√3、i)：Q]＝[Q(⁴√3、i)：Q(√3、i)]・[Q(√3、i)：Q(√3)]・[Q(√3)：Q]＝2・2・2＝8
• ＃(D₄)＝＃(L₄)・＃(S₂)・＃(I)＝4・2・1＝8

[3] T₂＝｛e、τ｝＝Gal(Q(⁴√3))

• τ(a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ )

＝a₀+ a₁x+ a₂x²+ a₃x³－a₄i－ix－ix²－ix³＝X

　　　a₄＝a₅＝a₆＝a₇＝0　

→　X＝a₀+ a₁x+ a₂x²+ a₃x³＝a₀+ a₁–⁴√3+ a_2-⁴√9+ a₃⁴√27　∊Q(⁴√3)

D₄⊃L₄⊃T₂⊃I　　⇔　Q⊂Q(√3)⊂Q(⁴√3)⊂Q(⁴√3,i)

[4] V₂＝｛e、τσ²｝＝Gal(Q(⁴√3i)/Q)を示します。

• τσ² (a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³ )

＝τ(a₀－a₁x＋a₂x²－a₃x³+ a₄i－a₅ix＋a₆ix²－a₇ix³)

＝a₀－a₁x＋a₂x²－a₃x³－a₄i＋a₅ix－a₆ix²+a₇ ix³＝X

　　a₁＝a₃＝a₄＝a₆＝0

　　→　X＝a₀+ a₂x²+a₅ix+ a₇ ix³＝a₀－a₂(⁴√3i)²+a₅(⁴√3i)－a₇(⁴√3i)³ ∊Q(⁴√3i)

D₄⊃L₄⊃V₂⊃I　　⇔　Q⊂Q(√3)⊂Q(⁴√3i)⊂Q(⁴√3,i)

[5] M₄＝｛e、σ²、τσ、τσ³｝＝Gal(Q(√3i)/Q)を示します。

・　σ²(X)＝Xより、X＝a₀＋a₂x² + a₄i＋a₆ix²

　　τσ(X)＝τσ(a₀＋a₂x² + a₄i＋a₆ix²)

　　　　　＝τ(a₀－a₂x² + a₄i－a₆ix²)

　　　　　＝a₀－a₂x²－a₄i＋a₆ix²＝a₀＋a₂x² + a₄i＋a₆ix²＝X

　　　    a₂＝a₄＝0　　→　X＝a₀＋a₆ ix²＝a₀＋a₆ √3i ∊ Q(√3i)

  D₄⊃M₄⊃S₂⊃I  ⇔　Q⊂Q(√3i)⊂Q(√3,i)⊂Q(⁴√3,i)

[6] U₂＝｛e、τσ｝＝Gal(Q((1－i)-⁴√3)) を示します。

・　τσ(X)＝τσ(a₀+ a₁x+ a₂x²+ a₃x³+ a₄i+a₅ix+a₆ix²+ a₇ ix³)

　　　　　＝τ(a₀+ a₁xi－a₂x²－ia₃x³+ a₄i－a₅x－a₆ix²+ a₇ x³)

　　　　　＝a₀－a₁xi－a₂x²＋ia₃x³－a₄i－a₅x＋a₆ix²+ a₇ x³＝X

　　　　a₁＝－a₅、a₂＝a₄＝0、a₃＝a₇、

　　　　　　→　X＝a₀+ a₁x+ a₃x³－a₁ix+a₆ix²+ a₃ ix³

　　　　　　　　　＝a₀+ a₁(1－i)x+ a₃(1＋i)x³+a₆ix²

　(1－i)²＝1－1－2i＝－2i、(1－i)³＝－2i(1－i)＝－2(i＋1)

X＝a₀+ a₁(1－i)x－1/2-a₃(1－i)³-x³－1/2-a₆(1－i)²-x² ∊ Q((1－i)-⁴√3))

• 　D₄⊃M₄⊃U₂⊃I　⇔　Q⊂Q(√3i)⊂Q((1－i)-⁴√3)⊂Q(⁴√3,i)

[7] W₂＝｛e、τσ³｝＝Gal(Q((1+i)-⁴√3)) を示します。

σ(x)＝ix、τ(x)＝x、σ(i)＝i、τ(i)＝－i、x＝⁴√3に注意して

　　σ²(X)＝Xより、X＝a₀＋a₂x² + a₄i＋a₆ix²

　　τσ³(X)＝τσ(a₀＋a₂x² + a₄i＋a₆ix²)　

　　　　　　＝τ(a₀－a₂x² + a₄i－a₆ix²)　

　　　　　　＝a₀－a₂x² －a₄i＋a₆ix²＝X＝a₀＋a₂x² + a₄i＋a₆ix²

　　　　　　a₂＝a₄＝0．　X＝a₀＋a₆ix²

　　(1＋i)²＝1－1＋2i＝2i、i＝1/2-(1＋i)²

　　　X＝a₀＋1/2-a₆ (1＋i)²x² ∊ Q((1＋i)-⁴√3)

• 　D₄⊃M₄⊃W₂⊃I　⇔　Q⊂Q(√3i)⊂Q((1＋i)-⁴√3)⊂Q(⁴√3,i)

ガロア群D₄が4つの解(1234)をどのように置換するかを調べます。

• D₄＝｛e、σ、σ²、σ³、τ、τσ、τσ²、τσ³｝

　＝｛e、(1324)、(12)(34)、(1423)、(34)、(14)(23)、(12)、(13)(24)｝

と表すことができます。

• f(t)＝t⁴－3＝(t²－⁴√9) ( t²＋⁴√9)＝(t－⁴√3) ( t＋⁴√3) ( t－⁴√3i) ( t＋⁴√3i)＝0

の4つの解は、改めてx=⁴√3とおくと

• （α₁、α₂、α₃、α₄）＝(x、－x、ix、－ix)と書けます。

σ(x)＝ix、τ(x)＝x、σ(i)＝i、τ(i)＝－i、の規則で4つの解を変換すると

• σ(x、－x、ix、－ix)＝(ix、－ix、－x、x)

⇔　σ(α₁、α₂、α₃、α₄)＝(α₃、α₄、α₂、α₁)

⇔　σ＝(1→3→2→4→1)＝(1324)

すなわちσは(1324)の置換作用素となっています。同様にして

• σ²(x、－x、ix、－ix)＝σ(ix、－ix、－x、x)＝(－x、x、－ix、ix)＝(α₂,α₁,α₄,α₃)

　　σ²＝(1→2→1、3→4→3)＝(12)(34)

すなわちσ²は12の互換と34の互換の作用素となっています。また

• σ³(x、－x、ix、－ix)＝σ²(ix、－ix、－x、x)＝σ(－x、x、－ix、ix)

＝(－ix、ix、x、－x)＝(α₄,α₃,α₁,α₂)

　　σ³＝(1→4→2→3→1)＝(1423)

すなわちσ³は(1423)の置換作用素となっています。τに関しても

• τ(x、－x、ix、－ix)＝(x、－x、－ix、ix)＝(α₁,α₂,α₄,α₃) ＝(34)

すなわちτは34の互換のみの作用素です。

• τσ(x、－x、ix、－ix)＝τ(ix、－ix、－x、x) ＝(－ix、ix、－x、x)＝(α₄,α₃,α₂,α₁)

　　τ＝(1→4→1、2→3→2)＝(14)(23)

すなわちτσは14の互換と23の互換の作用素となっています。

• τσ²(x、－x、ix、－ix)＝τ(－x、x、－ix、ix)＝(－x、x、ix、－ix)＝(α₂,α₁,α₃,α₄)

　　τσ²＝(12)　となっています。

• τσ³(x、－x、ix、－ix)＝τ(－ix、ix、x、－x)＝(ix、－ix、x、－x)＝(α₃,α₄,α₁,α₂)

　　τσ³＝(1→3→1、2→4→2)＝(13)(24) となっています。

＜まとめ＞

多項式f(x)＝x⁴－3の分解体とガロア群を求め、拡大体の系列と対応するガロア群の系列を7種類導出しました。f(x)の分解体はQ(⁴√3,i)であり、その上の有理数体を不変に保つQ自己同型写像全体は8次のD₄群となることを、群の演算表を作成して示しました。D₄の部分群には3つの4次の部分群と5つの2次の部分群がありました。部分群の作用で不変となる不変体を求めました。ガロア群に対応する不変体は拡大体の系列を構成することを示しました。

(1) D₄⊃K₄⊃S₂⊃I　⇔　Q⊂Q(i)⊂Q(√3,i)⊂Q(⁴√3,i)

(2) D₄⊃L₄⊃S₂⊃I  ⇔  Q⊂Q(√3)⊂Q(√3,i)⊂Q(⁴√3,i)

(3) D₄⊃L₄⊃T₂⊃I  ⇔ Q⊂Q(√3)⊂Q(⁴√3)⊂Q(⁴√3,i)

(4) D₄⊃L₄⊃V₂⊃I  ⇔ Q⊂Q(√3)⊂Q(⁴√3i)⊂Q(⁴√3,i)

(5) D₄⊃M₄⊃S₂⊃I  ⇔ Q⊂Q(√3i)⊂Q(√3,i)⊂Q(⁴√3,i)

(6) D₄⊃M₄⊃U₂⊃I  ⇔ Q⊂Q(√3i)⊂Q((1－i)-⁴√3)⊂Q(⁴√3,i)

(7) D₄⊃M₄⊃W₂⊃I  ⇔ Q⊂Q(√3i)⊂Q((1＋i)-⁴√3)⊂Q(⁴√3,i)

これまで多項式f(x) ＝x²－2とf(x)＝x⁴－4x²+16を例にとり、解を有理数体Qに加えて体を拡大し、拡大した体の上のQ同型写像と拡大体上の群を導く方法を説明しました。今回、ガロアの基本定理について述べ、Q多項式f(x)＝x³－2を例にとり、f(x)の分解体Q(³√2,ω)とガロア群S₃を求め、その中間体Q(ω)と部分群A₃がガロア対応していることを説明します。分かりやすい例を用いて、ガロアの基本定理を理解しましょう。

＜ガロアの基本定理＞

ガロアの基本定理とは、G＝Gal(L/Q)の部分群Hの個数とガロア拡大体L⊃K⊃Qなる中間体Kの個数は一致し、両者の間に全単射

• Φ：｛H｜{e}⊂H⊂G、Hは群｝　⇔　｛K｜L⊃K⊃Q、Kは体｝

が存在する。また＃(G)＝[L：Q]が成り立つ、というものです。例えば

• {e}⊂H₃⊂H₂⊂H₁⊂G　　⇔　L⊃K₃⊃K₂⊃K₁⊃Q

のように群H_iが体K_iに対応します。具体的には、Φ(H_i)＝K_iなる対応

• Φ(H)＝｛x｜x∊L、∀σ∊H、σ(x)＝x｝＝（群Hで動かない体Lの元の集合）＝L^H
• Φ^-1(K)＝｛σ｜σ∊G、∀x∊K、σ(x)＝x｝＝Kの元を動かさない群Gの元の集合＝G^K

を考えます。このような対応をガロア対応と言います。また

• HがGの正規部分群　⇔　KはQのガロア拡大体
• Gal(K/Q)＝G/H（剰余群）

が成り立っています。Qの拡大体K上のガロア群Gal(K/Q)は、Gの正規部分群HによるGの剰余群G/Hになっています。

• Gal(K₁/Q)＝G/H_1、Gal(K₂/K₁)＝H₁/ H_2、Gal(K₃/K₂)＝H₂/ H₃

が成り立っています。

• Φ({e})＝｛x｜x∊L、e (x)＝x｝＝L
• Φ(G)＝｛x｜x∊L、∀σ∊G、σ(x)＝x｝＝Q

が成り立ちます。正規部分群が単位群まで縮小したときに、最大の拡大体Lとなります。また最大群Gは拡大前の有理数体Qです。

Ex.2　　Q多項式f(x)＝x³－2を例に、f(x)の分解体とガロア群を求めてみましょう。

f(x)を因数分解すると

• f(x)＝x³－2＝(x－³√2)( x－³√2ω)( x－³√2ω²)、ω²＋ω＋1＝0、ω³＝1

となります。3つの解を、α₁＝³√2、α₂＝³√2ω、α₃＝³√2ω²、とします。

f(x)の分解体はQ(³√2,ω)となります。a_1、a_{2、・・・}a₆ ∊Q（有理数）を用いて

• Q(³√2,ω)＝｛a₁＋a₂³√2＋a₃³√4＋a₄ω＋a₅³√2ω＋a₆³√4ω｜a_i∊Q｝

と書けます。というのは、

• (³√2)²＝³√4、(³√2)³＝2、ω²＝－ω－1

なので、独立な基底は｛1. ³√2, ³√4, ω, ³√2ω, ³√4ω｝の6個になるからです。つまり

• [Q(³√2,ω)：Q]＝6

体の拡大次数は6となります。

• ω＝³√2ω/³√2＝­α₂/α₁＝­α₁²α₂/2、³√2ω＝α₂
• ³√4ω＝³√2³√2ω＝α₁α₂、³√4＝α₁²

ですから、

• Q(³√2,ω)＝｛a₁＋a₂α₁＋a₃α₁²＋a₄α₁²α₂/2＋a₅α₂＋a₆α₁α₂｜a_i∊Q｝＝Q(α₁,α₂)

と書くこともできます。Q(³√2,ω)上のQを不変にする自己同型写像σを考えます。

• 2＝σ(2)＝σ((³√2)³)＝σ(³√2)³→　σ(³√2)＝³√2、³√2ω、³√2ω²
• 0＝σ(0)＝σ(ω²＋ω＋1)＝σ(ω)²＋σ(ω)＋1　→　σ(ω)＝ω、ω²

ですから、自己同型写像σは

• σ₀：(³√2,ω)→(³√2,ω)
• σ₁：(³√2,ω)→(³√2ω,ω)
• σ₂：(³√2,ω)→(³√2ω²,ω)
• σ₃：(³√2,ω)→(³√2,ω²)
• σ₄：(³√2,ω)→(³√2ω,ω²)
• σ₅：(³√2,ω)→(³√2ω²,ω²)

の6つとなります。σ₀は恒等写像です。これらの写像を(α₁、α₂、α₃)に作用させると

• σ₁(α₁)＝σ₁(³√2)＝³√2ω＝α₂
• σ₁(α₂)＝σ₁(³√2ω)＝σ₁(³√2)σ₁ (ω)＝³√2ω・ω＝α₃
• σ₁(α₃)＝σ₁(³√2ω²)＝σ₁(³√2)σ₁ (ω²)＝³√2ω・ω²＝³√2＝α₁

よって、

• σ₁(α₁、α₂、α₃)＝(α₂、α₃、α₁)＝(1→2→3→1)＝(123)

なる解の置換を引き起こします。同様にして、

• σ₂(α₁)＝σ₂(³√2)＝³√2ω²＝α₃
• σ₂(α₂)＝σ₂(³√2ω)＝σ₂(³√2)σ₂ (ω)＝³√2ω²・ω＝α₁
• σ₂(α₃)＝σ₂(³√2ω²)＝σ₂(³√2)σ₂ (ω²)＝³√2ω²・ω²＝³√2ω＝α₂

よって、

• σ₂(α₁、α₂、α₃)＝(α₃、α₁、α₂)＝(3→2→1→3)＝(321)

なる解の置換を引き起こします。同様にして、

• σ₃(α₁)＝σ₃(³√2)＝³√2＝α₁
• σ₃(α₂)＝σ₃(³√2ω)＝σ₃(³√2)σ₃(ω)＝³√2・ω²＝α₃
• σ₃(α₃)＝σ₃(³√2ω²)＝σ₃(³√2)σ₃(ω²)＝³√2・ω⁴＝³√2ω＝α₂

よって、

• σ₂(α₁、α₂、α₃)＝(α₁、α₃、α₂)＝(2⇔3)＝(23)
• なる解α₂とα₃の互換を引き起こします。同様にして、σ₄：(³√2,ω)→(³√2ω,ω²)
• σ₄(α₁)＝σ₄(³√2)＝³√2ω＝α₂
• σ₄(α₂)＝σ₄(³√2ω)＝σ₄(³√2)σ₄(ω)＝³√2ω・ω²＝α₁
• σ₄(α₃)＝σ₄(³√2ω²)＝σ₄(³√2)σ₄(ω²)＝³√2ω・ω⁴＝³√2ω²＝α₃

よって、

• σ₄(α₁、α₂、α₃)＝(α₂、α₁、α₃)＝(1⇔2)＝(12)

なる解α₁とα₂の互換を引き起こします。同様にして、σ₅：(³√2,ω)→(³√2ω²,ω²)

• σ₅(α₁)＝σ₅(³√2)＝³√2ω²＝α₃
• σ₅(α₂)＝σ₅(³√2ω)＝σ₅(³√2)σ₅(ω)＝³√2ω²・ω²＝³√2ω＝α₂
• σ₅(α₃)＝σ₅(³√2ω²)＝σ₅(³√2)σ₅(ω²)＝³√2ω²・ω⁴＝³√2＝α₁

よって、

• σ₅(α₁、α₂、α₃)＝(α₃、α₂、α₁)＝(1⇔3)＝(13)

なる解α₁とα₃の互換を引き起こします。以上をまとめると

• G＝｛e、σ₁、σ₂、σ₃、σ₄、σ₅｝＝｛e、(123)、(321)、(23)、(12)、(13)｝＝S₃

Q(³√2,ω)上のQを不変にする自己同型写像は合成写像を演算として3次の対称群S₃をなすことが分かります。群Gの位数は6です。これは拡大体Q(³√2,ω)が6次元であることに対応しています。Gの部分群は、自明な{e}とS₃を除くと、A₃、B₂、C₂、D₂の4つです。

• A₃＝｛e、σ₁、σ₂｝＝｛e、(123)、(321)｝　⇔　A₃ はQ (ω)を不変にする群
• B₂＝｛e、σ₃｝＝｛e、(23) ｝　⇔　B₂はQ(α₁) を不変にする群
• C₂＝｛e、σ₄｝＝｛e、(12) ｝　⇔　C₂はQ(α₃) を不変にする群
• D₂＝｛e、σ₅｝＝｛e、(13) ｝　⇔　D₂はQ(α₂) を不変にする群

となります。A₃は正規部分群ですが、B₂は正規部分群ではありません。ガロア対応は

• Φ(S₃)＝Q、Φ(A₃)＝Q(ω)、Φ({e})＝Q(³√2,ω)

となっています。

σ₄＝(12)はα₁とα₂の互換を引き起こすので、Q(α₃)を不変にします。実際

• Q(³√2,ω)＝｛a₁＋a₂α₁＋a₃α₁²＋a₄α₁²α₂/2＋a₅α₂＋a₆α₁α₂｜a_i∊Q｝＝Q(α₁,α₂)
• σ₄(a₁＋a₂α₁＋a₃α₁²＋a₄α₁²α₂/2＋a₅α₂＋a₆α₁α₂)

＝a₁＋a₂α₂＋a₃α₂²＋a₄α₂²α₁/2＋a₅α₁＋a₆α₂α₁

a₂＝a_5、a₃＝a₄＝0であればσ₄の作用で不変になります。

σ₄(x)＝xの場合、x=a₁＋a₂(α₁＋α₂)＋a₆α₁α₂

となります。解と係数の関係

• α₁＋α₂＋α₃＝³√2(1+ω+ω²)＝0　→　α₁＋α₂＝－α₃
• α₁α₂α₃＝³√2・³√2ω・³√2ω²)­＝2　→　α₁α₂＝2/α₃

を代入すると、xはα₃だけに依存することを示すことができます

• x＝a₁＋a₂(α₁＋α₂)＋a₆α₁α₂＝a₁－a₂α₃＋2a₆/α₃∊ Q(α₃)

つまり、｛e,σ₄｝＝｛e,(12)｝はQ(α₃)を不変にします。σ₄＝(12)はα₁とα₂の互換を引き起こすので、Q(α₃)を不変にするのは明らかです。

次にA₃ はQ (ω)を不変にすることを示します。

σ₁＝(123)、σ₁：(³√2,ω)→(³√2ω,ω) 、ω²＝－(1+ω)

に注意すると

σ₁(a₁＋a₂³√2＋a₃³√4＋a₄ω＋a₅³√2ω＋a₆³√4ω)

＝a₁＋a₂³√2ω＋a₃³√4ω²＋a₄ω＋a₅³√2ω²＋a₆³√4ω²ω

＝a₁＋a₄ω＋a_2・³√2ω＋a_6・³√4－a_3・³√4(1+ω)－a_5・³√2(1+ω)

＝a₁＋a₄ω－a₅³√2＋(a₆－a₃)-³√4＋(a₂－a₅)-³√2ω－a_3・³√4ω

もとの元と係数を比較すると

• a₂＝－a₅、a₅＝a₂－a₅→　a₂＝a₅＝0
• a₃＝a₆－a₃、a₆＝－a₃→　a₃＝a₆＝0

よって

• σ₁(a₁＋a₄ω)＝a₁＋a₄ω ∊ Q(ω)

が示されました。同様に、σ₂：(³√2,ω)→(³√2ω²,ω)、ω²＝－(1+ω)に注意すると

σ₂(a₁＋a₂³√2＋a₃³√4＋a₄ω＋a₅³√2ω＋a₆³√4ω)

＝a₁＋a₂³√2ω²＋a₃³√4ω⁴＋a₄ω＋a₅³√2ω²ω＋a₆³√4ω⁴ω

＝a₁＋a₂³√2ω²＋a₃³√4ω＋a₄ω＋a₅³√2＋a₆³√4ω²

＝a₁－a₂³√2(1+ω)＋a₃³√4ω＋a₄ω＋a₅³√2－a₆³√4(1+ω)

＝a₁ ＋(a₅－a₂)-³√2－a_6・³√4＋a₄ω－a_2・³√2ω＋(a₃－a₆)-³√4ω

σ₂ (　)内と係数を比較すると

・a₂＝a₅－a_2、a₅＝－a₂→　a₂＝a₅＝0

・a₃＝－a_6、a₆＝a₃－a₆→　a₃＝a₆＝0

よって

• σ₂(a₁＋a₄ω)＝a₁＋a₄ω ∊ Q(ω)

が示されました。つまり、

A₃＝｛e、σ₁、σ₂｝はQ(ω)を不変にする群である

ことが分かりました。以上をまとめます。

• S₃＝{e,σ₁,σ₂,σ₃,σ₄,σ₅}⊃ A₃＝{e,σ₁,σ₂} ⊃ {e}：ガロア群の縮小列
• Q　⊂　Q(ω)　⊂　Q(³√2,ω) ；体のガロア拡大
• Φ(S₃)＝Q、Φ(A₃)＝Q(ω)、Φ({e})＝Q(³√2,ω)：ガロア対応
• [Q(ω)：Q]＝2、[Q(³√2,ω)：Q(ω)]＝3、体の拡大次元
• [Q(³√2,ω)：Q]＝[Q(³√2,ω)：Q(ω)]・[Q(ω)：Q]＝3・2＝6
• S₃/ A₃＝{I A₃,J A₃} 、A₃/ {e}＝{e E,σ₁E,σ₂E }：2つの剰余群
• ＃(S₃)＝＃(S₃/ A₃)・＃(A₃/{e})＝3・2＝6　：剰余群の位数の積は対称群の位数に等しい

ここではガロア理論を理解するための基本事項について解説します。まず多項式x²－2の根√2を用いて有理数体QをQ(√2)に拡大し、Q(√2)上の同型写像が満たすべき条件について調べます。Q(√2)は基底｛1、√2｝を有する2次元の拡大体であり、Q(√2)上のQ同型写像は2次の巡回群｛e、σ₁｝を成します。併せてQ(³√2)が体であることを確認する方法を示します。代数方程式の解による拡大体とその上の同型写像が作る群には密接な関係があり、拡大体の次元と群の位数は一致します。次に多項式分解体によるガロア拡大とその上の同型写像によるガロア群について説明し、簡単な例を示します。Q上の4次の規約多項式f(x)＝x⁴－4x²+16の分解体Q(√3、i)を求め、Q(√3、i)が4次の拡大体であり、その上のQ同型写像からなるガロア群が4元の互換変換群であることを確認します。

＜体の拡大とその上の同型写像について＞

有理数の全体をQとします。Qに√2を添加した体を

• Q(√2)＝｛a+b√2｜a,b∊Q｝⊃Q

と書きます。Q(√2)は四則演算で

• (a+b√2)+(c+d√2)＝a+c+(b+d)√2 ∊ Q(√2)
• (a+b√2)・(c+d√2)＝ac－2bd+(ad+bc)√2 ∊ Q(√2)
• 1/(a+b√2)＝(a－b√2)/(a+b√2) (a－b√2)＝(a－b√2)/(a²－2b²) ∊ Q(√2)

閉じているのでQの拡大体となっています。

√2の最小多項式はx²－2です。√2はx²－2＝0の解なので、2次の代数的数と呼びます。a,b∊Qに対して、1a+b√2＝0ならばa=b=0となるので、1と√2はQ(√2)の独立な基底となっています。つまりQ(√2)は2次元のベクトル空間と同型です。QからQ(√2)への拡大の次数を[Q(√2)：Q]と表すと、[Q(√2)：Q]＝2となります。

拡大体Q(√2)上のQ自己同型写像σについて考えます。Q自己同型写像σは任意のQの元xを不変に保つQ(√2)からQ(√2)への全単射写像です。

• σ：Q(√2) → Q(√2)、σ(x)＝x for ∀x ∊ Q

また同型写像は和と積の演算を保存します。

• σ(x+y)＝σ(x)+σ(y)、σ(xy)＝σ(x)σ(y)　 for ∀x ∊ Q(√2)

従って

• σ(1)＝1、σ(0)＝0、σ(n)＝n、σ(－n)＝－n、σ(q/p)＝q/p

が成り立ちます。つまり有理数xに対して

• σ(x)＝x for ∀x ∊ Q

が成り立っています。以下にそれを示しましょう。例えば

• σ(1)＝σ(1・1)＝σ(1)σ(1) → σ(1)(σ(1)－1)＝0 → σ(1)＝0またはσ(1)＝1

もしσ(1)＝0とすると、任意のx ∊ Q(√2)に対して、

• σ(x)＝σ(x・1)＝σ(x)σ(1)＝0　

となり、σが全単射写像であることに矛盾します。従って

• σ(1)＝1

となります。また

• σ(0)＝σ(0+0)＝σ(0)+σ(0)　→　σ(0)＝0

です。ｎ＝1+1+1+・・・+1（ｎ個の1の和）を代入すると

• σ(n)＝σ(1+1+・・+1)＝σ(1)＋σ(1)+・・+σ(1)＝1+1+・・+1＝n

です。

• 0＝σ(0)＝σ(n－n) ＝σ(n)+σ(－n)　→　σ(－n)＝－n
• q=σ(pq/p)＝σ(p) σ(q/p)＝pσ(q/p) →　σ(q/p)＝q/p

となっています。

それではQ上で同型を保つようにσの√2に対する作用を考えてみましょう。

• 2＝σ(2)＝σ(√2・√2)＝σ(√2)σ(√2) →　σ(√2)＝√2、－√2

となります。∀a,b∊ Qに対して

• σ₀(√2)＝√2の場合、σ₀(a+b√2)＝σ₀(a)+σ₀(b)σ₀(√2)＝a+b√2

なので、σ₀は恒等写像eです。

• σ₁(√2)＝－√2の場合、σ₁(a+b√2)＝σ₁(a)+σ₁(b)σ₁(√2)＝a－b√2

となります。拡大体Q(√2)上のQ同型写像は｛e、σ₁｝となります。

• σ_1・σ₁(√2)＝σ₁(－√2)＝－(－√2)＝√2＝e (√2)　→　σ_1・σ₁＝e

となるので｛e、σ₁｝は合成写像の二項演算に関して2次の巡回群をなします。

Q上の代数方程式x²－2=0の解√2を用いて有理数体QをQ(√2)に拡大しました。Q(√2)は基底｛1、√2｝を有する2次元の拡大体であり、Q(√2)上のQ同型写像は2次の巡回群｛e、σ₁｝を成すことが分かりました。代数方程式の解による拡大体とその上の同型写像が作る群には密接な関係があり、拡大体の次元と群の位数は一致します。

次に有理数Qに三乗根³√2を添加した拡大体を考えます。

• (³√2)²＝³√4∉Q、(³√2)³＝2∊Q

なので、³√4が³√2と同時に付加され、

• Q(³√2)＝｛a+b³√2+c³√4｜a,b｝⊃Q

となります。Q(³√2)は加減乗除について閉じているので体となります。

• a+b³√2+c³√4＋a’+b’³√2+c’³√4＝(a+a’)+(b+b’)³√2+(c+c’)³√4 ∊ Q(³√2)
• (a+b³√2+c³√4)(a’+b’³√2+c’³√4)=(aa’+2bc’ +2b’c)+(ab’+a’b+2cc’) ³√2+(ac’+a’c+2bb’) ³√4 ∊ Q(³√2)

Q(³√2)が割り算について閉じていることを示すのには少し計算が必要です。

• 1/(a+b³√2+c³√4)＝a’+b’³√2+c’³√4　∊ Q(³√2)を示します。

　　1/(a+b³√2+c³√4)＝1/c・1/[³√4+(b/c)³√2+(a/c)]

α＝³√2とおきます。改めてb/cをb、a/cをcとおいて

• 1/(α²+bα+c)＝αの2次式 ∊ Q(³√2)

になることを示せばよいことが分かります。

∃a_1、a_2、k、r ∊Q　なる有理数が存在して

• x³－2＝(x－a₁)(x²+bx+c)+k(x－a₂)
• (x²+bx+c)＝(x－a₂) (x－a₃)+r

が成立します。よって、2式から(x－a₃)を消去すると

• (x²+bx+c)＝(x－a₂) [x³－2－(x－a₁)(x²+bx+c)]/k+r
• [1+(x－a₂) (x－a₁)/k] (x²+bx+c)＝(x－a₂)(x³－2)/k＋r

となります。上式にαを代入すると、α³－2＝0より、右辺はｒのみになるので、

• 1/(α²+bα+c)＝[1+(α－a₂) (α－a₁)/k]/r＝(1/rk)[α²－(a₁＋a₂)α+ a₁a₂+k] ∊ Q(³√2)

が示されます。つまりQ(³√2)は割り算について閉じていることが分かります。

＜多項式分解体とガロア群について＞

数αを根とする最小次数のモニック多項式を最小多項式といいます。例えば√2の最小多項式はｘ²－2です。モニック多項式とはｘ²+2ｘ+3の様に最大次数の項の係数が1である多項式のことです。

KがQの有限次数の拡大体とします。Kの任意の元αの最小多項式の全ての解がKの元であるとき、KをQのガロア拡大体あるいは正規拡大体K/Qと言います。

Q(有理数)係数のｎ次多項式f(x)の全ての根α₁,α₂,α₃,…α_nを加えた拡大体Q(α₁,α₂,α₃,…α_n)をf(x)の多項式分解体と言います。実は、ここでは証明しませんが、KがQ係数の多項式分解体であることはKがQの正規拡大体であることと同値になっています。

今KがQの正規拡大体とします。K上のQ自己同型な写像Aut(K)をKのガロア群といい、Gal(K/Q)と書きます。同じことですが、KがQ係数多項式f(x)の分解体のとき、Aut(K)をf(x)のガロア群といい、Gal(f)と書きます。任意のQの元xに対して、σ∊Gal(f)はσ(x)＝xである自己同型写像なので、f(x)＝0の解α₁,α₂,α₃,…α_nに関して

• f(σ(α_i))＝σ(f(α_i))＝σ(0)＝0　for i=1,2,…n

が成り立ちます。σ(α₁),σ(α₁)・・σ(α_n)はf(x)＝0の解になっています。つまり

• σ(α₁),σ(α₁)・・σ(α_n)　⇔　α_σ(1),α_σ(2) ,α_σ(3) …,α_σ(n)

と同一視すると、σで解を変換することは、解の順番を入れ替えることに相当します。

Ex1.　Q多項式f(x)＝x⁴－4x²+16を例に、f(x)の分解体とガロア群を求めてみましょう。

f(x)＝x⁴－4x²+16はQ上ではこれ以上因数分解できない規約多項式です。f(x)の分解体とはf(x)＝0の解をQに付け加えてできた拡張体のことでした。f(x)を因数分解すると

• f(x)＝x⁴－4x²+16＝(x²＋4)²－(2√3x)²＝(x²＋2√3x＋4)( x²－2√3x＋4)
• 　　＝(x－α₁) (x－α₂) (x－α₃) (x－α₄)
• α₁＝√3＋i、α₂＝√3－i、α₃＝－√3＋i、α₄＝－√3－i

となります。解をQに付加すると

• Q(√3＋i、√3－i、－√3＋i、－√3－i)＝Q(√3,i)

すなわちf(x)の分解体はQ(√3,i)になります。

ちなみにQ(√3,i)＝Q(√3＋i)も成立します。

• t＝√3＋iとおくと、t²＝2＋2√3i、t³＝(2＋2√3i)( √3＋i)＝8i

　　　→　i= t³/8、√3＝t－i＝t－t³/8

より、√3とiは√3＋iで表すことができるからです。

結局Q(√3,i)は4つの基底[1,i,√3,√3i]をもつ4次元ベクトル空間と同型でした。Q(√3,i)上の同型写像σは、Qの元は不変に保ち、iと√3は符号を変える変換を含みます。つまり

• －1＝σ(－1)＝σ(ii)＝σ(i)σ(i)　→　σ(i)＝±i
• 3＝σ(3)＝σ(√3√3)＝σ(√3)σ(√3)　 →　σ(√3)＝±√3

でした。よってQ(√3,i)の元

• a+bi+c√3+d√3i　∊Q(3,i)　for a,b,c,d∊Q

に対するQ同型写像σとして

• σ₁(a+bi+c√3+d√3i)＝a＋bi＋c√3＋d√3i：恒等写像e
• σ₂(a+bi+c√3+d√3i)＝a－bi＋c√3－d√3i：(i,√3)→(－i,＋√3)
• σ₃(a+bi+c√3+d√3i)＝a＋bi－c√3－d√3i：(i,√3)→(＋i,－√3)
• σ₄(a+bi+c√3+d√3i)＝a－bi－c√3＋d√3i：(i,√3)→(－i,－√3)

の4種類のQ同型写像が考えられます。今

• σ_iσ_j＝σ_jσ_ifor i,j=1,2,3,4
• σ_iσ_i＝e、σ₁σ_i＝σ_i for i=1,2,3,4
• σ₁σ₂＝σ₃、σ₁σ₃＝σ₂、σ₂σ₃＝σ₁

が成り立つので｛e＝σ₁,σ₂,σ₃,σ₄｝はクラインの4元群(Z/2Z×Z/2Z)になります。

具体的にσの解に対する作用を調べてみましょう。

• σ₂(α₁)＝σ₂(√3＋i)＝√3－i＝α₂
• σ₂(α₂)＝σ₂(√3－i)＝√3＋i＝α₁
• σ₂(α₃)＝σ₂(－√3＋i)＝－√3－i＝α₄
• σ₂(α₄)＝σ₂(－√3－i)＝－√3＋i＝α₃

つまり、σ₂は

• σ₂(α_1、α_2、α_3、α₄)＝(α_2、α_1、α_4、α₃)＝（12）（34）

1と2、3と4の互換変換となります。同様に

• σ₃(α₁)＝σ₃(√3＋i)＝－√3＋i＝α₃
• σ₃(α₂)＝σ₃(√3－i)＝－√3－i＝α₄
• σ₃(α₃)＝σ₃(－√3＋i)＝√3＋i＝α₁
• σ₃(α₄)＝σ₃(－√3－i)＝√3－i＝α₂

つまり、

• σ₃(α_1、α_2、α_3、α₄)＝(α_3、α_4、α_1、α₂)＝（13）（24）

1と3、2と4の互換変換となります。同様に

• σ₄(α₁)＝σ₄(√3＋i)＝－√3－i＝α₄
• σ₄(α₂)＝σ₄(√3－i)＝－√3＋i＝α₃
• σ₄(α₃)＝σ₄(－√3＋i)＝√3－i＝α₂
• σ₄(α₄)＝σ₄(－√3－i)＝√3＋i＝α₁

つまり、

• σ₄(α_1、α_2、α_3、α₄)＝(α_4、α_3、α_2、α₁)＝（14）（23）

1と4、2と3の互換変換となります。

結局、f(x)＝x⁴－4x²+16のガロア群Gは

• G＝｛e,σ₂,σ₃,σ₄｝＝｛e,(12)(34),(13) (24),(14)(23)｝

なる互換変換の群であることが分かりました。また

• ＃G＝4（群の個数）　⇔　[Q(√3、i)：Q]＝4（拡大次数）

が成り立っていることが確認できました。Q上の4次の規約多項式f(x)＝x⁴－4x²+16の分解体Q(√3、i)を求め、Q(√3、i)が4次の拡大体であり、その上のQ同型写像からなるガロア群が4元の互換変換群であることを確認しました。

今日は5次以上の方程式は代数的に解けないことを示します。ガロア理論によれば、方程式が代数的に解けるということは、方程式のガロア群が可解群であるということでした。従ってｎ≧5のとき、S_n⊃A_n⊃N⊃・・・⊃Eなる正規群Nが存在するかを調べます。

対称群S_nは（1,2,3、・・・n）の全ての解の置換の集合です。A_nは偶置換群ですから、S_n⊃A_nは常に成り立ちます。A_n⊃Nなる正規群Nが存在すると仮定して、Nはどんな性質をもっているかを調べます。正規群Nの共役元はNに属します。つまり任意の

• t∊N、a∊A_nに対して、ata^-1∊N

でした。Nは群ですから、ata^-1t^-1∊Nも成り立ちます。ata^-1t^-1を交換子といいます。交代群A_nに含まれる循環置換のタイプは以下の4種類です。

(1)4次以上の巡回置換を含む置換　

　　t＝(0123…)……

(2) 3次の巡回置換を含む置換　

　　t＝(012)(34…)…

(3) 3次の巡回置換

　　t＝(012)

(4)2つの互換を含む置換

　　t＝(01)(23)…

互換は奇置換なので2つないと偶置換になりません。Nはこの中のどれかの循環置換タイプだと考えられます。最も単純な循環置換a＝(123)、(124)・・∊A_nによって、t∊Nの交換子ata^-1t^-1∊Nがどのような循環タイプに属するかを調べます。

a=(124)＝(1→2→4→1)、t＝(01)＝(0→1→0)の意味であることに注意して下さい。初期の順列01234…がata^-1t^-1の作用で変化する様子を調べます。

[1] t＝(012)(34…)…∊N、a＝(124) ∊A_nのとき

　　　　　　　　   　　　　    01234…（初期順列）

　a=(1→2→4)　    　　　　     02431…（aの作用後の順列）

　t=(0→1→2)(3→4→p…)…　10p42…（tの作用後の順列）

　a^-1=(1←2←4)　　　　　　  40p21…（a^-1の作用後の順列）

   t^-1=(0←1←2)(3←4←p…)…  32410…（t^-1の作用後の順列）

ata^-1t^-1によって、初期の順列が01234…から32410…に変化したので、

• ata^-1t^-1＝(0→3→1→2→4)＝(03124) ：5次の巡回置換

と書けます。Nに3次の巡回置換を含む置換が含まれている場合、必ずNに5次の巡回置換が含まれていることが分かりました。これは4次以上の巡回置換を含む置換に含まれます。それでは4次以上の巡回置換は交換子でどのように変換されるでしょうか？

[2] t＝(0123…)…∊N、a＝(123) ∊A_nのとき

　　　　　　　　   　　　　    01234…（初期順列）

   a=(1→2→3)　    　　　　      02314…（aの作用後の順列）

　t=(0→1→2→3→4→p…)…    1342p…（tの作用後の順列）

　a^-1=(1←2←3)　　　　　　    3241p…（a^-1の作用後の順列）

   t^-1=(0←1←2←3←4←p…)…    21304…（t^-1の作用後の順列）

よって、

• ata^-1t^-1＝(0→2→3→0→2)＝(023) ：3次の巡回置換

Nに4次以上の巡回置換を含む置換が含まれている場合、Nには必ず3次の巡回置換が含まれることが分かりました。3次の巡回置換は交換子でどのように変換されるでしょうか？

[3] t＝(012)∊N、a＝(123) ∊A_nのとき

　　　　　　　　   　　  01234…（初期順列）

    a=(1→2→3)　    　　   02314…（aの作用後の順列）

　t=(0→1→2)　　　　　10324…（tの作用後の順列）

　a^-1=(1←2←3)　　　　 30214…（a^-1の作用後の順列）

   t^-1=(0←1←2)　   　　　32104…（t^-1の作用後の順列）

よって、

• ata^-1t^-1＝(0→3→0)(1→2→1)＝(03)(12) ：2つの独立な互換の積

Nに3次の巡回置換が含まれている場合、Nには必ず2つの独立な互換の積があることが分かりました。それでは独立な互換の積は交換子でどのように変換されるでしょうか？

[4] t＝(01)(23)∊N、a＝(123) ∊A_nのとき

　　　　　　　　   　　   0123…（初期順列）

    a=(1→2→3)　    　　    0231…（aの作用後の順列）

　t=(0→1)(2→3)…　　　 1320…（tの作用後の順列）

　a^-1=(1←2←3)　　　　  3210…（a^-1の作用後の順列）

   t^-1=(0←1)(2←3)…　　　2301…（t^-1の作用後の順列）

よって、

• ata^-1t^-1＝(0→2→0)(1→3→1)＝(02)(13) ：2つの独立な互換の積

Nに独立な互換の積が含まれている場合、必ず2つの独立な互換の積がNに含まれることが分かりました。[1]～[4]の結果、Nには、少なくとも1つの独立な互換の積が含まれていることを示しています。

[5]任意の独立な互換積(jk)(mn)は正規群Nに含まれていることを示します。

Nに含まれている1つの独立な互換の積を(12)(34)とします。1234以外の数から任意の数jkmnを選び、偶置換aをつくります。

    a＝(jkmn/1234/pqrs)＝(j→1→p、k→2→q、m→3→r、n→4→s)∊A_n

　t＝(12)(34)＝(1→2→1)(3→4→3)∊N

  a^-1＝(pqrs/1234/jkmn)＝(j←1←p、k←2←q、m←3←r、n←4←s)∊A_n

NはA_nの正規部分群なのでata^-1∊Nです。

　　　　　　　　   　　     1234jkmn…（初期順列）

   a=(jkmn/1234/pqrs)        pqrs1234…（aの作用後の順列）

　t=(1→2)(3→4)　　　　   pqrs2143…（tの作用後の順列）

　a^-1=(pqrs/1234/jkmn)　 1234kjnm…（a^-1の作用後の順列）

よって

　ata^-1＝(1234jkmn/1234kjnm)＝(jkmn/kjnm) ＝(jk)(mn)∊N

Nには少なくとも1つの独立な互換の積があるので、Nには任意の独立な互換の積が含まれることが示されました。

[6]独立でない互換の積もNに含まれることを示します。

独立でない互換の積として(12)(13)があります。これは1がどちらにも入っているので独立ではありません。これも偶置換なのでA_nに含まれています。(12)(13)はNに含まれているでしょか？　5次以上の置換群には、123の3解以外にも2解があります。それを45として、置換(45)を考えます。正規群Nには任意の独立な互換が含まれているので

• (12)(45)、 (45) (13)∊N　→　(12)(45)・(45)(13)＝(12)(13)∊N

が成り立ちます。つまり正規群Nはすべての独立でない互換の積も含みます。交代群A_nは全ての互換の積の集合ですから、結局ｎ≧5のときA_nの正規部分群Nは交代群A_n自身に他なりません。5次以上の交代群は正規の真部分群を含んでいないので、ガロア系列に分解できる可解群ではないことが示されました。ガロアが方程式の解という無限アナログの世界を解の群という有限デジタルの世界に引き戻したことで、高次方程式の解の公式を求める無駄な努力を省くことに成功しました。今日ガロアが編み出した群は様々な分野に応用されています。

ガロアは小学校に馴染めず、ずっとお母さんに勉強を教わっていました。15歳で数学と出会い、17歳で方程式論の論文を科学アカデミ－に提出しますが、コ－シ－に紛失され、再度書き改めた論文を受けたフ－リエが急逝してしまいます。受験に2度失敗して、街の名士であるお父さんが自殺して、絶望したガロアは革命運動に関わり、投獄されます。20歳の時に療養所で出会ったステファニ－という女性と出会いますが、他の男に決闘を申し込まれて、負傷したまま見捨てられ死んでしまいます。ガロアは自分の成果を称賛されたことは一度もありませんでした。天才はどんな境遇でも成果を残しますが、その生涯は本当に可哀そうです。

4次方程式を題材にしてガロア理論を紹介します。

＜フェラ－リの4次方程式の解法＞

4次方程式は、平行移動で3次の項を消去できるので、一般にp,q,r∊Q[有理数]を用いて

• x⁴+px²+qx+r＝0　　・・・（A1）

と書き表せます。両辺に2kx²+k²を付け加え、4次の項を平方完成させると

• x⁴+2kx²+k²＝(2k－p)x²－qx
• (x²＋k) ²＝(2k－p)(x－q/2(2k－p))²＋k²－r－q²/ 4(2k－p)
• (x²＋k) ²＝(2k－p)(x－q/2(2k－p))²＋D(k)/4(2k－p)

となります。ここで判別式を

• D(k)＝(k²－r) (2k－p) －q²＝2k³－pk²－2rk＋pr＝0　　・・・（A1）

としました。この3次方程式を解いて、解kを代入すると

・(x²＋k) ²＝(2k－p)(x－q/2(2k－p))²

を得ます。ここで

• m＝√(2k－p)、n＝－q/[2√(2k－p)]　

とおくと上式は

• (x²＋k) ²－(mx+n) ²＝0
• (x²＋mx＋k＋n) (x²－mx＋k－n) ＝0

より

• x²＋mx＋k＋n＝0
• x²－mx＋k－n＝0

と書けます。この2次方程式の判別式は、それぞれ

　D₁＝m²－4k－4n

　D₂＝m²－4k＋4n

です。2つの2次方程式を解くと、結局4次方程式（A1）の解は

• x₁＝[－m＋√(m²－4k－4n)]/2＝[－m＋√D₁]/2
• x₂＝[＋m－√(m²－4k＋4n)]/2＝[＋m－√D₂]/2
• x₃＝[－m－√(m²－4k－4n)]/2＝[－m－√D₁]/2
• x₄＝[＋m＋√(m²－4k＋4n)]/2＝[＋m＋√D₂]/2

となります。ここで、k＝k(p,r)は3次方程式

• 2k³－pk²－2rk＋pr＝0　　・・・（A2）

の解であり、

　k－p/6＝u(p,r)+v(p,r)、ωu +ω²v 、ω²u+ωv

m、nは

• m＝√(2k(p,r)－p)、n＝－q/[2√(2k(p,r)－p)]、

であります。

＜4次方程式のガロア群＞

3次方程式の解をu³,v³とすると、3次方程式の場合と同様に、有理数に1の三乗根を付加した固定体Qωを

• Qω⊂Qω[u]⊂Qω[u, u³]

と拡大することで3次方程式の解が得られます。さらに2つの判別式の項を加えて

• Qω⊂Qω[u³]⊂Qω[u, u³] ⊂Qω[u, u³, √D₁]⊂Qω[u, u³, √D₁, √D₂]

と拡大することで、4つの4次方程式の解が得られます。Qω[u, u³, √D₁, √D₂]は固定体Qωのガロア拡大体です。5つの拡大体列に対応する5つのガロア群の縮小正規列は

・S₄（対称群）⊃A₄（交代群）⊃ B₄⊃ C₂ ⊃ E＝｛I｝

となります。A₄はQω[u³]のガロア群、B₄はQω[u,u³]のガロア群、C₂はQω[u, u³, √D₁] のガロア群です。それぞれの体と群の対応をガロア対応といいます。

n次方程式の解が四則演算と冪乗根で表せるガロア拡大体の数であるためには、ガロア拡大体に対応するガロア群の縮小列があって、全ての剰余群が巡回群でなければなりません。4次方程式の場合には上のようなガロア対応が成り立っており、全ての剰余群が巡回群なので、代数的に解くことができます。ガロア群の縮小列が形成できなければ、代数的に解くことはできません。

＜4次方程式のガロア群の生成元＞

解の入れ替えに関する写像は以下のI,J,K,L,Mの5通りです。J,K,L,Mは4次方程式のガロア群を生成する元です。

I：恒等写像　                 ：(1234/1234)

J：u → v → u　             ：(1234/2134)＝(12)

K：u+v →ωu +ω²v →ω²u+ωv：(1234/2314)＝(123)

L：(x_1, x_2, x_3, x₄)→(x_4, x_3, x_2, x₁)　：(1234/4321)＝(14)(23)　；(n,m)→(－n,－m) →(n,m)

M：(x_1, x_2, x_3, x₄)→(x_3, x_4, x_1, x₂)　：(1234/3412)＝(13)(24)　：　√　→ －√　→ √

• x₁＝[－m＋√(m²－4k－4n)]/2＝[－m＋√D₁]/2
• x₂＝[＋m－√(m²－4k＋4n)]/2＝[＋m－√D₂]/2
• x₃＝[－m－√(m²－4k－4n)]/2＝[－m－√D₁]/2
• x₄＝[＋m＋√(m²－4k＋4n)]/2＝[＋m＋√D₂]/2

4次方程式の4つの解の入れ替え写像は、2つの解の入れ替え写像の合成演算により、対称群S₄をなします。4元の入れ替えは4！＝24通りあります。まずはL、Mの演算について調べてみましょう。

LM＝(1234/4321) (1234/3412)＝(1234/4321)(4312/2143) ＝(1234/2143)＝(12)(34)

つまり、LMは1⇔2、3⇔4の交換を行います。(x_1, x_2, x_3, x₄)の2組の互換は、M、L、LMの3つしかありません。

ML＝(1234/3412) (1234/4321)＝(1234/3412) (3412/2143)＝(1234/2143)＝(12)(34)＝ML

MM＝(1234/3412) (1234/3412)＝ (1234/3412) (3412/1234)＝(1234/1234)＝I

LL= (1234/4321) (1234/4321)＝(1234/4321) (4321/1234)＝(1234/1234)＝I

なので

• B₄＝｛I、M、L、LM｝

は群をなします。ML=LMなので、B₄は可換群です。B₄はJ,Kとは可換なので、S₃の正規部分群になっています。またB₄の全ての元は遇置換です。B₄はQω[u, u³]のガロア群です。Qω[u, u³]によってkの値が固定されても、(x_1, x_2, x_3, x₄)は影響を受けません。B4の部分群について調べてみましょう。

• E＝｛I｝⊂　C₂＝｛I、M｝⊂B₄

C₂はS₃の正規部分群になっています。

LL＝Iなので、剰余類B₄/ C₂は巡回群です。√D1の最小多項式の次数は2です。

• B₄/ C₂＝｛I C₂、L C₂｝

MM＝Iなので、剰余類C₂/Eは巡回群です。√D2の最小多項式の次数は2です。

• C₂/E＝｛EI、EM]｝

対称群S₄は、4！＝24個の元からなり、

• S₄＝JA₄∪I A₄
• A₄＝｛I、K、K²｝・｛I、M、L、LM｝＝｛I、K、K²｝・B₄
• B₄＝｛I、L｝・｛I、M｝＝｛I、L｝・C₂

の様に分解できます。A₄は12個の元からなる交代群（遇置換群）です。JA₄は群ではありません。

A₄＝｛I、M、L、LM、、KI、KM、KL、KLM、、K²I、K²M、K²L、K²LM｝

JA₄＝｛J、JM、JL、JLM、、JKI、JKM、JKL、JKLM、、JK²I、JK²M、JK²L、JK²LM｝

剰余類S₄/ A₄は巡回群になっています。

• S₄/ A₄＝｛I A₄、JA₄｝

剰余類の要素の数を位数といいます。S₄/ A₄の位数は2です。剰余類の位数は、対応する代数体に加えた数の最小多項式の次数と一致します。補助方程式を解くためにu³（＝√）をQωに加えたのですが、u³の最小多項式は2次なので、位数2と一致しています。

剰余類A₄/ B₄は、K B₄＝B₄ Kなので、巡回群になっています。

• A₄/ B₄＝｛I B₄、K B₄、K² B₄｝

A₄はQω[u,u³]のガロア群です。u³、v³からu、vを出すためにuを加えました。Uの最小多項式は3次なので、剰余類A₄/ B₄の位数3に対応しています。

以上、4次方程式を解いて、そのガロア群について調べてみました。4次方程式の解の入れ替えに関して縮小するガロア群の列が形成でき、その剰余類が一つの元から生成せれる巡回群だったので、4次方程式の場合はガロア拡大体に解を見出すことができることが確かめられました。

エバリスト・ガロアはフランスの天才数学者です。20歳の死の直前に書かれた1832年の書簡で、5次以上の方程式は代数的に解くことができないことを群論を用いて示しました。ガロアの理論は難解ですぐには理解されませんでしたが、後世の数学に大きな影響を与えました。ガロア理論とはどのようなものなのでしょうか？

＜3次の対称群S₃＞

ガロア理論では代数方程式の解を並び替える写像を考えます。三次方程式の3つの解を(123)とすると、（123）を並び替える写像は3！＝6個あります。2つの並び替えを連続して行った結果は1つの並び替えになるので、その合成写像は群の演算となります。(123)の6つの並び替え写像を要素とする集合は3次の対称群S₃になります。

ここでは1→2、2→3、3→1に並び替える巡回写像Kを（123／231）と表記します。同様に1→2、2→1、3→3に並び替える互換写像Jを（123／213）と定義します。恒等写像はI＝(123／123)です。すなわち

・　I＝(123／123)、K＝（123／231）＝（231）、J＝（123／213）＝（12）

この表示法を用いると、合成写像は

KJ＝（123／231）（123／213）＝（123／231）（231／132）＝（123／132）＝（23）

と計算できます。ここで（123／213）＝（231／132）と書き換えました。つまりこの合成写像の演算は（123）→（231）→（132）の並び替えであり、結局2と3の入れ替えになります。一方

• JK＝(123／213)(123／231)＝(123／213)( 213／321)＝(123／321)＝(13)

となります。JK≠KJ、つまりJとKは可換ではありません。

もっと簡略化した表記では、K＝(231)、J＝(12)と書きます。これは(231)が(2→3→1→2)なる並び替え、(12)は1と2の交換を表しています。簡略表記では

• KJ＝(231)(12)＝(23)

と書けますが簡略表記で演算計算をしない方がいいでしょう。同様に他の演算は

• K²＝ (123／231)(123／231)＝(123／231) (231／312)＝(123／312)＝(312)
• K³＝(123／312) (123／231)＝(123／312) (312／123)＝(123／123)＝I
• JK²＝(123／213)(123／312)＝(123／213)( 213／132)＝(123／132)＝(23)

となります。つまり、JKは互換(13)、JK²は互換(23)となります。互換は奇数置換です。奇置換同士の合成演算は奇置換となるので閉じています。巡回KやK²は偶数置換です。遇置換も合成演算に関して閉じています。結局S₃の部分群は

• E＝｛I｝
• C₂＝｛I、J｝＝｛I、(12)｝
• A₃＝｛I、K、K²｝＝｛I、(231)、(312)｝

の3つです。A₃は遇置換の部分集合で、交代群と呼ばれています。C₂もA₃も1つの元で作られる巡回群です。

＜正規部分群＞

群Gの部分群HがGの任意の元aに対して、

• 　aHa^-1＝H

が成り立つとき、部分群HをGの正規部分群と言います。これは集合として

• ｛aha^-1｜h∊H｝＝{ ah₁a^-1, ah₂a^-1,ah₃a^-1,・・・ ah_na^-1}＝｛h₁,h₂,h₃,・・・h_n｝

等しいことを意味しているのであって、すべての元で

• ah_ka^-1＝h_k

が成り立つわけではありません。実際I、K、K²∊A₃⊂S₃に対して

JIJ^-1＝I

JKJ^-1＝(123/213)(123/231) (123/213)＝(123/321) (321/312) ＝( 123／312)＝K²

JK²J^-1＝(123/213)(123/312) (123/213)＝(123/132) (132/231) ＝( 123／231)＝K

が成り立つので、A₃はS₃の正規部分群です。しかしJ∊C₂に対して

• KJK^-1＝ (123/231) (123/213) (123/312)＝(123/132) (132/321)＝(123/321)＝(13)∉C₂

なので、C₂はS₃の正規部分群ではありません。

＜剰余群S₃/ A₃＞

対称群S₃＝｛I、K、K²、J、JK、JK²｝は、2つの集合

• I A₃＝｛I、K、K²｝（遇置換）、J A₃＝｛J、JK、JK²｝（奇置換）

に分割できます。

• S₃ ＝I A₃∪J A₃、かつI A₃∩J A₃＝空集合

A₃は正規部分群なので、A₃による剰余群

• S₃/ A₃＝｛I A₃、J A₃｝

が定義できます。剰余群の要素I A₃、J A₃を剰余類と呼びます。JA₃は群ではありません。

・JK・JK＝JKJ^-1・K＝K²K＝I ∉JA₃

任意のa,b∊S₃に対して、A₃b＝b A₃が成り立つので、

• aA₃・bA₃＝a・A₃b・A₃＝a・b A₃・A₃＝ab A₃

より、正規部分群による商は群になります。実際

• I A₃・J A₃＝J A₃、J A₃・J A₃＝I A₃

なので、剰余群S₃/ A₃は群になっています。JA₃が生成元になって剰余群のすべての要素が作られるので、剰余群S₃/ A₃は巡回群になっています。

また同様に剰余群A₃/E＝｛IE、KE、K²E｝も、KEが生成元になって剰余群のすべての要素が作られるので、巡回群になっています。実は剰余群がｎ次の巡回群であることは、n次方程式が

• zⁿ＝1
• z_k＝cos(2πk/n)+i・sin(2πk/n) k=0,1,2,・・・n-1

という形で解けることを意味しています。

3次方程式の解の対称群S₃の正規部分群A₃とEからなる全ての剰余群S₃/ A₃とA₃/Eが巡回群なので、解を表現する代数体を拡大することで、3次方程式

• x³＋px＋q＝0

は代数的に解けることになります。

＜三次方程式と巡回群＞

前回、3次方程式には、x＝u+vなる解があり、u³とv³が2次方程式

• t²＋qt－(p/3)³＝0

の解になっていることから、

• u³＝－q/2＋√D、v³＝－q/2－√D
• D＝(q/2)²＋(p/3)³

と表せることを示しました。有理数Qにω³＝1の根ωを付け加えた代数体Qωを考えます。さらに√Dを付け加えた拡大体をとQω(u³)します。u³とv³を入れ替えることは、√Dの係数1を-1に入れ替えることに相当します。1と-1は1の2乗根であり、x²－1＝(x－1)(x＋1)＝0の2解になっています。剰余群S₃/ A₃＝｛I A₃、J A₃｝は√Dの係数1を-1に巡回させる変換に対応付けられます。解を構成する代数体をQωからQω(u³)に拡大すると、解が受ける群はS₃からA₃に縮小されます。さらにuを付け加えると拡大体Qω(u,u³)が得られます。Qω(u,u³)上の3つの解は、

• α＝u+v、β＝ωu+ω²v、γ＝ω²u+ωv

です。前回示したように変換K

• K(u)＝ωu、K(v)＝ω²v

を用いると、3つの解は

• K(α)＝β、K(β)＝γ、K(γ)＝α

と巡回変換されます。解を入れ替えることは、u、vの係数を1、ω、ω²と変化させることに対応します。これらは1の3乗根であり、x³－1＝(x－1)(x－ω)(x－ω²)＝0の3解になっています。剰余群A₃/E＝｛IE、KE、K²E｝は、3つの解を巡回させる変換Kが作る巡回群に対応付けられます。解を構成する代数体をQω(u³)からQω(u,u³)に拡大すると、解が受ける群はA₃からEに縮小します。方程式を代数的に解く工程は、解の受ける対称群を巡回群に分解することに相当します。対称群を巡回群に分解できなければ、方程式を代数的に解くことはできません。

　エバリスト・ガロアは、一般の5次方程式では、解の遇置換である交代群A₅に正規部分群が存在しないので、巡回群が形成できず、代数体の拡大によって、5次方程式を代数的に解くことができないことを示しました。

剰余類の最も身近な例は偶数と奇数です。整数Zは遇数と奇数に分けられます。偶数と奇数は、整数Zの正規部分群であり、

• Z＝2Z∪(2Z+1)、2Z∩(2Z+1) ＝空集合

ですから、剰余群Z/2Zの剰余類です。

• Z/2Z＝｛2Z、2Z+1｝

と表せます。

＜代数学の基本定理とは＞

1799年にフリ－ドリヒ・ガウスは学位論文の中でn次の複素多項式

• F(z)＝zⁿ+a_n-1 z^n-1 + a_n-2 z^n-2+・・・+a₁z+a₀＝0

は、n個の複素解を持つことを証明しました。これは代数学の基本定理と呼ばれています。この定理の証明には実解析的な証明あるいはリウヴィルの定理やルーシェの定理（1862年）を用いた複素関数論的な証明があります。

リウヴィルの定理によると全複素平面において有界かつ解析的な複素関数は定数でなければなりません。任意の z ∈C に対し、F(z)≠0 とすると、G(z) = 1/F(z) は有界な整関数となり、リウヴィルの定理により、F(z) は定数関数となり、仮定に矛盾します。だからF(z)＝0となるz∈Cが存在するというものです。

ルーシェの定理によると複素関数f(z)とg(z)が領域Dの境界で｜f(z)｜＞｜g(z)｜であるなら、D内でf(z)+g(z)とf(z)の零点の個数は一致しなければなりません。ここで

• f(z)＝zⁿ
• g(z)＝a_n-1 z^n-1 + a_n-2 z^n-2+・・・+a₁z+a₀

とすると、半径Rの円領域Dの境界では、｜f(z)｜＞｜g(z)｜となり、ルーシェの定理により、D内でのF(z)＝f(z)+g(z)＝0の零点の個数は、zⁿ＝0の零点の個数nに一致します。複素関数論的な証明は簡潔ですが、複素関数論に馴染みがないと、代数学の基本定理を納得するのは容易ではありません。

ガウスはどのように代数学の基本定理を証明したのでしょうか？　今回、ｎ次方程式の実部と虚部を描画して解となる交点の個数を調べてみました。Re(F(x,y))＝0とIm(F(x,y))＝0のグラフがｎ個の交点をもつことから、ｎ次の代数方程式F(z)＝0にｎ個の複素数解が存在することが直感的に分かりました。

＜ガウスの証明方法＞

• F(z)＝zⁿ+a_n-1 z^n-1 + a_n-2 z^n-2+・・・+a₁z+a₀＝0

に対して

• z＝r(cos(nφ)+i・sin(nφ))、r>0
• a_n-1＝A(cosα＋i・sinα)、A>0
• a_n-2＝B(cosβ＋i・sinβ、B>0
• a₀＝L(cosλ＋i・sinλ)、L>0

とおいて代入すると、実部と虚部は

Re(F(z))＝rⁿ cos(nφ)+A r^n-1 cos[(n-1)φ+α]+ B r^n-2 cos[(n-2)φ+β]+・・+Lcosλ

Im(F(z))＝rⁿ sin(nφ)+A r^n-1 sin[(n-1)φ+α]+ B r^n-2 sin[(n-2)φ+β]+・・+Lsinλ

となります。

[補題]　このとき十分大きなRを取ると、

• rⁿ－√2（A r^n-1＋B r^n-2＋・・+L）＞0　for r＞R

が成り立つ。

[証明]　rⁿで割ると

• 1－√2・（A/r＋B/r²＋・・・+L/ rⁿ）＞0
• 1－√2・M（1/r＋1/r²＋・・・+1/ rⁿ）＞0　、M＝max｛A,B,・・・L｝

を示せばよいことになります。今、半径R=1+√2・Mとおくと、r＞Rより

• r＞1+√2・M　→　r－1＞√2・M　→　1－√2・M/(r-1)＞0
• 1/r＋1/r²＋・・・+1/ rⁿ　＜　(1/r)/(1-1/r)＝1/(r-1)
• 1－√2・M（1/r＋1/r²＋・・・+1/ rⁿ）＞1－√2・M/(r-1)＞0

が示されます。

[1] Re(F(z))＝0の線は、複素平面の半径ｒ＞R＝1+√2・max｛A,B,・・・L｝の円を2n個の円弧に分割し、Re(F(z))は円弧上で交互に正負の値を取る。

[証明1]

半径ｒ＞Rの円上に偏角φ＝2π/4nで4n個の点P₀、P₁、・・P_2ｋ-1、P_2ｋ、P_2ｋ+1・・P_4ｎ-1を取ります。最初の点P₀の偏角はπ/4nとし、P₁（3π/4n）、P₂（5π/4n）とします。（πは円周率パイのこと）

P_2ｋの偏角φ_2k＝π/4n＋2π/4n・2k＝(kπ+π/4)/nであるから、Re(F(z))の第一項の cos(nφ)の値は、cos(nφ)＝cos(kπ+π/4)＝cos(kπ) cos(π/4)＝(－1)^k/√2　となります。

同様にP_2ｋ+1の偏角φ_2k+1＝π/4n＋2π/4n・(2k+1)＝(kπ+3π/4)/nであるから、cos(nφ)＝cos(kπ+3π/4)＝cos(kπ) cos(3π/4)＝－(－1)^k/√2　となります。点P_2ｋと点P_2ｋ+1では、rⁿ cos(nφ)の符号が異なります。補題より

• rⁿ/√2＞ A r^n-1＋B r^n-2＋・・+L

ｋが偶数のとき

Re(F(z=P_2ｋ))＞rⁿ cos(nφ_2ｋ)－(A r^n-1＋B r^n-2＋・・+L）＞rⁿ/√2－rⁿ/√2＝0

Re(F(z=P_2ｋ+1))＜rⁿ cos(nφ_2ｋ+1)＋(A r^n-1＋B r^n-2＋・・+L)＜－rⁿ・/√2＋rⁿ/√2＝0

ｋが奇数の時

Re(F(z=P_2ｋ))＜rⁿ cos(nφ_2ｋ)+A r^n-1＋B r^n-2＋・・+L＜－rⁿ/√2＋rⁿ/√2＝0

Re(F(z=P_2ｋ+1))＞rⁿ cos(nφ_2ｋ+1)－(A r^n-1＋B r^n-2＋・・+L)＞rⁿ/√2－rⁿ/√2＝0

つまり、半径r＞Rの円の2n個の円弧上でRe(F(z))は交互に正負の値をとります。

[2] Im(F(z))＝0の線は、複素平面の半径ｒ＞R＝1+√2・max｛A,B,・・・L｝の円を2n個の円弧に分割し、Im(F(z))は円弧上で交互に正負の値を取る。

[証明2]

P_2ｋの偏角φ_2k＝π/4n＋2π/4n・2k＝(kπ+π/4)/nだから、Im(F(z))の第一項の sin(nφ_2k)の値は、sin(nφ_2k)＝sin(kπ+π/4)＝cos(kπ) sin(π/4)＝(－1)^k/√2　　となります。

同様にP_2ｋ－1の偏角φ_2k-1＝π/4n＋2π/4n・(2k－1)＝(kπ－π/4)/nだから、sin(nφ_2k-1)＝sin(kπ－π/4)＝－cos(kπ) sin(π/4)＝－(－1)^k/√2　　　　　　　となります。点P_2ｋと点P_2ｋ-1では、rⁿ sin(nφ)の符号が異なります。補題より

• rⁿ/√2＞ A r^n-1＋B r^n-2＋・・+L

ｋが偶数の時

Im(F(z=P_2ｋ))＞rⁿ sin(nφ_2ｋ)－(A r^n-1＋B r^n-2＋・・+L)＞rⁿ/√2－rⁿ/√2＝0

Im(F(z=P_2ｋ-1))＜rⁿ sin(nφ_2ｋ-1)＋A r^n-1＋B r^n-2＋・・+L＜－rⁿ/√2＋rⁿ/√2＝0

ｋが奇数の時

Im(F(z=P_2ｋ))＜rⁿ sin(nφ_2ｋ)+A r^n-1＋B r^n-2＋・・+L　＜－rⁿ/√2＋rⁿ/√2＝0

Im(F(z=P_2ｋ-1))＞rⁿ sin(nφ_2ｋ-1)－(A r^n-1＋B r^n-2+・・+L)＞rⁿ/√2－rⁿ/√2＝0

つまり、半径r＞Rの円の2n個の円弧上でIm(F(z))は交互に正負の値をとります。

[3]  Re(F(z))は円弧上で交互に正負の値を取るため、中間値の定理より、Re(F(z))＝0の線は、複素平面の半径ｒ＞Rの円と2n個の点で交差します。Im(F(z))は円弧上で交互に正負の値を取るため、中間値の定理より、Im(F(z))＝0の線は、複素平面の半径ｒ＞Rの円と2n個の点で交差します。円の内部に入り込んだRe(F(z))＝0の線とIm(F(z))＝0の線はｎ個の交点z_k (k=1,2,…,n) をもちます。ｎ個の交点z_kではF(z_k)＝Re(F(z_k))＋i・Im(F(z_k))＝0となるので、z_k (k=1,2,…,n)はｎ次方程式の解になっています。

[3]の証明は難しいので、いくつかｎ次方程式の例を用いて、Re(F(z))＝0の線とIm(F(z))＝0の線がｎ個の交点z_k (k=1,2,…,n) をもつことを確かめることにしましょう。

＜10次の方程式の例＞

• F(z)＝z¹⁰+z⁹+ z⁸+ z⁷+ z⁶+z⁵+ z⁴+ z³+ z²+z＝0

について考えます。この方程式はz=0,－1なる実解を持ちます。

• F(z)＝z(z⁹+ z⁸+ z⁷+ z⁶+z⁵+ z⁴+ z³+ z²+z+1)＝0
• z¹⁰－1＝(z－1)( z⁹+ z⁸+ z⁷+ z⁶+z⁵+ z⁴+ z³+ z²+z+1)＝0
• z₀=0、z_k＝cos(kπ/5)+i・sin(kπ/5) （k=1,2,3,4,5,6,7,8,9）、z₅＝－1

他の8個の解はｒ＝1の円上にある偏角kπ/5（k=1,2,3,4,6,7,8,9）の複素解です。

図1に複素平面上にRe(F(z))＝0の黒線とIm(F(z))＝0の赤線を示します。緑色の放射状の領域はRe(F(z))＞0の領域で、青緑色の領域はRe(F(z))＜0の領域を示しています。黄緑色の放射状の領域はIm(F(z))＞0の領域で、緑色の領域はIm(F(z))＜0の領域を示しています。これらの2つのグラフを重ね合わせます。

図2にｒ＝3（＞1+√2・1）の円を4n＝40分割した図を示します。Re(F(z=P_2k))＞0、Re(F(z=P_2k+1))＜0となっており、P_2kとP_2k+1の間にRe(F(z_2k))＝0となる点があり、Re(F(z))＝0の線はz_2kを通過しています。同様にIm(F(z=P_2k))＜0、Im(F(z=P_2k-1))＞0となっており、P_2kとP_2k-1の間にRe(F(z_2k-1))＝0となる点があり、Re(F(z))＝0の線はz_2k-1を通過しています。Re(F(z))＝0の線とIm(F(z))＝0の線は円の内部で10個の交点z_k (k=1,2,…,10) をもつことが確かめられます。

＜5次方程式の例1＞

• F(z)＝z⁵+ z³+z＝z(z⁴+ z²+1)＝0

を考えます。ｚ＝0を解に持ちます。

• z⁶－1＝(z²－1)( z⁴+ z²+1)＝0

が成り立つので、

z⁴+ z²+1＝0　の解は、z⁶－1＝0の6個の解の内ｚ＝1,－1を除いた4個の解です。

　z_k＝cos(kπ/3)+i・sin(kπ/3)　（k＝1,2,4,5）

　　＝(1+√3i)/2、(－1+√3i)/2、(－1－√3i)/2、(1－√3i)/2

図3で赤線はIm(F(x,y))＝0の線、黒線はRe(F(x,y))=0の線を表しています。赤線と黒線の交点がF(x,y)＝0の解となります。Re(F(x,y))≅rⁿcos(nφ)、Im(F(x,y)) ≅rⁿsin(nφ)なので、位相がπ/2回転しています。

＜5次方程式の例2＞

• F(z)＝z⁵+ z³+2z²+1＝0

を考えます。5次方程式なので実数解を持ちます。図4に5つの解の位置を示します。赤線と黒線の交点がF(x,y)＝0の解となります。2次の係数が2なので、解はｒ＝1の円上に並んでいません。5次方程式にはRe(F(x,y)) とIm(F(x,y))が正となる領域が5つ放射状に広がっています。Re(F(x,y))の正領域とIm(F(x,y))の正領域がπ/2回転してずれているので、Re(F(x,y))＝0の黒線とIm(F(x,y))＝0の赤線が5つの交点を持ちます。

Re(F(x,y))＝0とIm(F(x,y))＝0のグラフがｎ個の交点をもつことから、ｎ次の代数方程式F(z)＝0にｎ個の複素数解が存在することが直感的に分かります。

中学生になると無理数を学びます。無理数は英語で「不合理な数（irrational number）」といいます。1：1：√2の直角三角形の斜辺の長さは無理数です。無理数を発見したのはピタゴラス教団の一人です。ピタゴラスは数の調和を崇拝していたので、分数で書き表せない数を認めませんでした。ピタゴラスは神聖な数を冒涜した罪で無理数を発見した仲間を死刑にしてしまいます。

2乗して2になる性質をもつことは、√2が存在することを保証しません。√2＝1.414213562・・・と無限に続きます。√2は、

　{1.4、1.41、1.414、1.4142、1.41421、・・・}

と無限に続く（極限で収束する）有理数の数列と同一視されます。つまり無理数は無限の有理数の集合と同一視して創られた数なのです。

数は簡単に作ることができます。例えば整数を3で割った余りが0になる整数の集合を[0]と書くと、整数を{[0]、[1] 、[2]}の3つの集合に分けることができます。これを新たな3つの数と見なし、加減乗除を定義することができます。この場合も数は無限の要素を持つ集合と同一視して創られます。

現代数学では多項式をも数と見なします。整数の世界で成り立つ様々な定理は、多項式の世界の定理として成り立ちます。数学者は真偽が分からない定理（予想）の場合、先に多項式世界で真偽を確かめようとします。

多項式が数になるとはどういうことでしょうか？　例えば多項式をｘ²－2で割った余りで分類してみましょう。例えばｘ⁴＋ｘ－4の場合は

• ｘ⁴＋ｘ－4＝（ｘ²＋2）・（ｘ²－2）＋ｘ
• ｘ⁴－2＝（ｘ²＋2）・（ｘ²－2）＋2

となります。多項式の割り算など何の役に役に立つのか分かりませんでしたが、実は重要な役割を果たしているのです。ここで

• Rx＝{ｘ²－2で割った余りがｘになるすべての多項式}
• R2＝{ｘ²－2で割った余りが2になるすべての多項式}

なる集合を考えます。ｘ⁴＋ｘ－4はRxに含まれる多項式、ｘ⁴－2はR2に含まれる多項式の一つであることが分かります。ｘ²をｘ²－2で割った余りは2だから

• ｘ²＝1・（ｘ²－2）＋2
• Rx・Rx＝R2　⇔　ｘ・ｘ＝2

が成り立ちます。大胆に集合R2を数2だと見なすと、多項式ｘ²－2を法とする世界では、（無限の多項式からなる集合）Rxは√2に相当する数になるのです。

現代数学では、頑張って方程式を解くのではなく、方程式を使って数を創造することで、方程式と解を同時に求めてしまいます。頭の固い人には、神聖なる数を冒涜しているように映るかもしれません。私たちは、柔軟な考えに興味を示すように、子どもたちを育てていかなければなりません。