<代数学の基本定理とは>
1799年にフリ-ドリヒ・ガウスは学位論文の中でn次の複素多項式
- F(z)=zn+an-1 zn-1 + an-2 zn-2+・・・+a1z+a0=0
は、n個の複素解を持つことを証明しました。これは代数学の基本定理と呼ばれています。この定理の証明には実解析的な証明あるいはリウヴィルの定理やルーシェの定理(1862年)を用いた複素関数論的な証明があります。
リウヴィルの定理によると全複素平面において有界かつ解析的な複素関数は定数でなければなりません。任意の z ∈C に対し、F(z)≠0 とすると、G(z) = 1/F(z) は有界な整関数となり、リウヴィルの定理により、F(z) は定数関数となり、仮定に矛盾します。だからF(z)=0となるz∈Cが存在するというものです。
ルーシェの定理によると複素関数f(z)とg(z)が領域Dの境界で|f(z)|>|g(z)|であるなら、D内でf(z)+g(z)とf(z)の零点の個数は一致しなければなりません。ここで
- f(z)=zn
- g(z)=an-1 zn-1 + an-2 zn-2+・・・+a1z+a0
とすると、半径Rの円領域Dの境界では、|f(z)|>|g(z)|となり、ルーシェの定理により、D内でのF(z)=f(z)+g(z)=0の零点の個数は、zn=0の零点の個数nに一致します。複素関数論的な証明は簡潔ですが、複素関数論に馴染みがないと、代数学の基本定理を納得するのは容易ではありません。
ガウスはどのように代数学の基本定理を証明したのでしょうか? 今回、n次方程式の実部と虚部を描画して解となる交点の個数を調べてみました。Re(F(x,y))=0とIm(F(x,y))=0のグラフがn個の交点をもつことから、n次の代数方程式F(z)=0にn個の複素数解が存在することが直感的に分かりました。
<ガウスの証明方法>
- F(z)=zn+an-1 zn-1 + an-2 zn-2+・・・+a1z+a0=0
に対して
- z=r(cos(nφ)+i・sin(nφ))、r>0
- an-1=A(cosα+i・sinα)、A>0
- an-2=B(cosβ+i・sinβ、B>0
- a0=L(cosλ+i・sinλ)、L>0
とおいて代入すると、実部と虚部は
Re(F(z))=rn cos(nφ)+A rn-1 cos[(n-1)φ+α]+ B rn-2 cos[(n-2)φ+β]+・・+Lcosλ
Im(F(z))=rn sin(nφ)+A rn-1 sin[(n-1)φ+α]+ B rn-2 sin[(n-2)φ+β]+・・+Lsinλ
となります。
[補題] このとき十分大きなRを取ると、
- rn-√2(A rn-1+B rn-2+・・+L)>0 for r>R
が成り立つ。
[証明] rnで割ると
- 1-√2・(A/r+B/r2+・・・+L/ rn)>0
- 1-√2・M(1/r+1/r2+・・・+1/ rn)>0 、M=max{A,B,・・・L}
を示せばよいことになります。今、半径R=1+√2・Mとおくと、r>Rより
- r>1+√2・M → r-1>√2・M → 1-√2・M/(r-1)>0
- 1/r+1/r2+・・・+1/ rn < (1/r)/(1-1/r)=1/(r-1)
- 1-√2・M(1/r+1/r2+・・・+1/ rn)>1-√2・M/(r-1)>0
が示されます。
[1] Re(F(z))=0の線は、複素平面の半径r>R=1+√2・max{A,B,・・・L}の円を2n個の円弧に分割し、Re(F(z))は円弧上で交互に正負の値を取る。
[証明1]
半径r>Rの円上に偏角φ=2π/4nで4n個の点P0、P1、・・P2k-1、P2k、P2k+1・・P4n-1を取ります。最初の点P0の偏角はπ/4nとし、P1(3π/4n)、P2(5π/4n)とします。(πは円周率パイのこと)
P2kの偏角φ2k=π/4n+2π/4n・2k=(kπ+π/4)/nであるから、Re(F(z))の第一項の cos(nφ)の値は、cos(nφ)=cos(kπ+π/4)=cos(kπ) cos(π/4)=(-1)k/√2 となります。
同様にP2k+1の偏角φ2k+1=π/4n+2π/4n・(2k+1)=(kπ+3π/4)/nであるから、cos(nφ)=cos(kπ+3π/4)=cos(kπ) cos(3π/4)=-(-1)k/√2 となります。点P2kと点P2k+1では、rn cos(nφ)の符号が異なります。補題より
- rn/√2> A rn-1+B rn-2+・・+L
kが偶数のとき
Re(F(z=P2k))>rn cos(nφ2k)-(A rn-1+B rn-2+・・+L)>rn/√2-rn/√2=0
Re(F(z=P2k+1))<rn cos(nφ2k+1)+(A rn-1+B rn-2+・・+L)<-rn・/√2+rn/√2=0
kが奇数の時
Re(F(z=P2k))<rn cos(nφ2k)+A rn-1+B rn-2+・・+L<-rn/√2+rn/√2=0
Re(F(z=P2k+1))>rn cos(nφ2k+1)-(A rn-1+B rn-2+・・+L)>rn/√2-rn/√2=0
つまり、半径r>Rの円の2n個の円弧上でRe(F(z))は交互に正負の値をとります。
[2] Im(F(z))=0の線は、複素平面の半径r>R=1+√2・max{A,B,・・・L}の円を2n個の円弧に分割し、Im(F(z))は円弧上で交互に正負の値を取る。
[証明2]
P2kの偏角φ2k=π/4n+2π/4n・2k=(kπ+π/4)/nだから、Im(F(z))の第一項の sin(nφ2k)の値は、sin(nφ2k)=sin(kπ+π/4)=cos(kπ) sin(π/4)=(-1)k/√2 となります。
同様にP2k-1の偏角φ2k-1=π/4n+2π/4n・(2k-1)=(kπ-π/4)/nだから、sin(nφ2k-1)=sin(kπ-π/4)=-cos(kπ) sin(π/4)=-(-1)k/√2 となります。点P2kと点P2k-1では、rn sin(nφ)の符号が異なります。補題より
- rn/√2> A rn-1+B rn-2+・・+L
kが偶数の時
Im(F(z=P2k))>rn sin(nφ2k)-(A rn-1+B rn-2+・・+L)>rn/√2-rn/√2=0
Im(F(z=P2k-1))<rn sin(nφ2k-1)+A rn-1+B rn-2+・・+L<-rn/√2+rn/√2=0
kが奇数の時
Im(F(z=P2k))<rn sin(nφ2k)+A rn-1+B rn-2+・・+L <-rn/√2+rn/√2=0
Im(F(z=P2k-1))>rn sin(nφ2k-1)-(A rn-1+B rn-2+・・+L)>rn/√2-rn/√2=0
つまり、半径r>Rの円の2n個の円弧上でIm(F(z))は交互に正負の値をとります。
[3] Re(F(z))は円弧上で交互に正負の値を取るため、中間値の定理より、Re(F(z))=0の線は、複素平面の半径r>Rの円と2n個の点で交差します。Im(F(z))は円弧上で交互に正負の値を取るため、中間値の定理より、Im(F(z))=0の線は、複素平面の半径r>Rの円と2n個の点で交差します。円の内部に入り込んだRe(F(z))=0の線とIm(F(z))=0の線はn個の交点zk (k=1,2,…,n) をもちます。n個の交点zkではF(zk)=Re(F(zk))+i・Im(F(zk))=0となるので、zk (k=1,2,…,n)はn次方程式の解になっています。
[3]の証明は難しいので、いくつかn次方程式の例を用いて、Re(F(z))=0の線とIm(F(z))=0の線がn個の交点zk (k=1,2,…,n) をもつことを確かめることにしましょう。
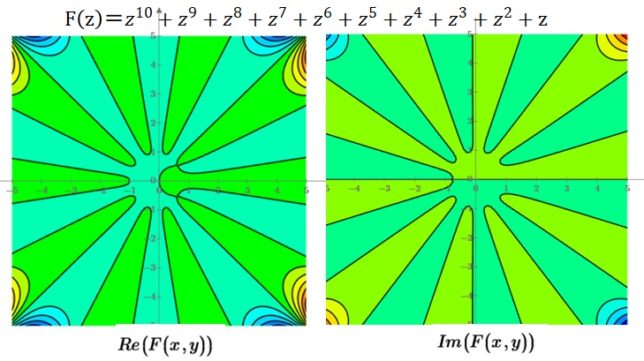
<10次の方程式の例>
- F(z)=z10+z9+ z8+ z7+ z6+z5+ z4+ z3+ z2+z=0
について考えます。この方程式はz=0,-1なる実解を持ちます。
- F(z)=z(z9+ z8+ z7+ z6+z5+ z4+ z3+ z2+z+1)=0
- z10-1=(z-1)( z9+ z8+ z7+ z6+z5+ z4+ z3+ z2+z+1)=0
- z0=0、zk=cos(kπ/5)+i・sin(kπ/5) (k=1,2,3,4,5,6,7,8,9)、z5=-1
他の8個の解はr=1の円上にある偏角kπ/5(k=1,2,3,4,6,7,8,9)の複素解です。
図1に複素平面上にRe(F(z))=0の黒線とIm(F(z))=0の赤線を示します。緑色の放射状の領域はRe(F(z))>0の領域で、青緑色の領域はRe(F(z))<0の領域を示しています。黄緑色の放射状の領域はIm(F(z))>0の領域で、緑色の領域はIm(F(z))<0の領域を示しています。これらの2つのグラフを重ね合わせます。
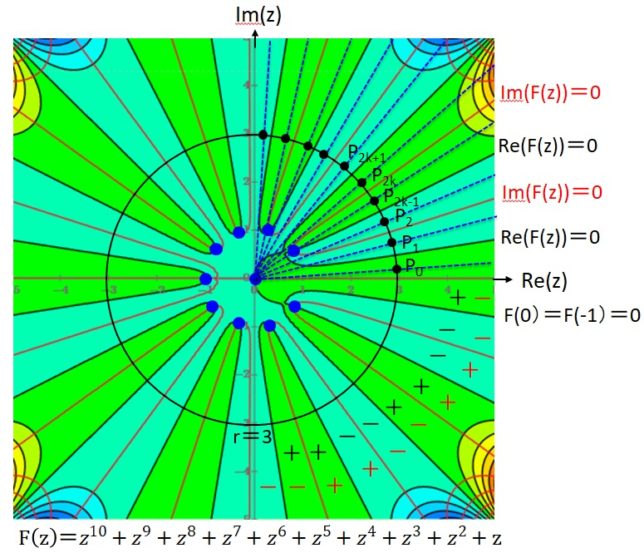
図2にr=3(>1+√2・1)の円を4n=40分割した図を示します。Re(F(z=P2k))>0、Re(F(z=P2k+1))<0となっており、P2kとP2k+1の間にRe(F(z2k))=0となる点があり、Re(F(z))=0の線はz2kを通過しています。同様にIm(F(z=P2k))<0、Im(F(z=P2k-1))>0となっており、P2kとP2k-1の間にRe(F(z2k-1))=0となる点があり、Re(F(z))=0の線はz2k-1を通過しています。Re(F(z))=0の線とIm(F(z))=0の線は円の内部で10個の交点zk (k=1,2,…,10) をもつことが確かめられます。
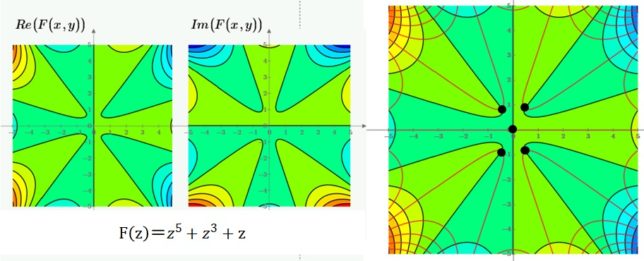
<5次方程式の例1>
- F(z)=z5+ z3+z=z(z4+ z2+1)=0
を考えます。z=0を解に持ちます。
- z6-1=(z2-1)( z4+ z2+1)=0
が成り立つので、
z4+ z2+1=0 の解は、z6-1=0の6個の解の内z=1,-1を除いた4個の解です。
zk=cos(kπ/3)+i・sin(kπ/3) (k=1,2,4,5)
=(1+√3i)/2、(-1+√3i)/2、(-1-√3i)/2、(1-√3i)/2
図3で赤線はIm(F(x,y))=0の線、黒線はRe(F(x,y))=0の線を表しています。赤線と黒線の交点がF(x,y)=0の解となります。Re(F(x,y))≅rncos(nφ)、Im(F(x,y)) ≅rnsin(nφ)なので、位相がπ/2回転しています。
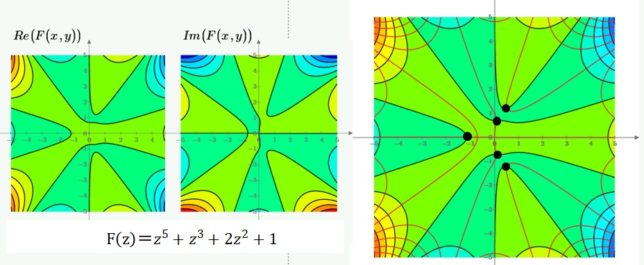
<5次方程式の例2>
- F(z)=z5+ z3+2z2+1=0
を考えます。5次方程式なので実数解を持ちます。図4に5つの解の位置を示します。赤線と黒線の交点がF(x,y)=0の解となります。2次の係数が2なので、解はr=1の円上に並んでいません。5次方程式にはRe(F(x,y)) とIm(F(x,y))が正となる領域が5つ放射状に広がっています。Re(F(x,y))の正領域とIm(F(x,y))の正領域がπ/2回転してずれているので、Re(F(x,y))=0の黒線とIm(F(x,y))=0の赤線が5つの交点を持ちます。
Re(F(x,y))=0とIm(F(x,y))=0のグラフがn個の交点をもつことから、n次の代数方程式F(z)=0にn個の複素数解が存在することが直感的に分かります。