＜マンゴルトの明示公式＞

前回チェビシェブ関数の積分表示

   Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} ζ'(s)/ζ(s)・x^s/s ds

を求めました。今回は積分を実行し、マンゴルトの明示公式を導出します。

　f_x(s)＝ζ'(s)/ζ(s)・x^s/s

とおくと

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds＝－1/2πi・∫_C1 f_x(s)ds

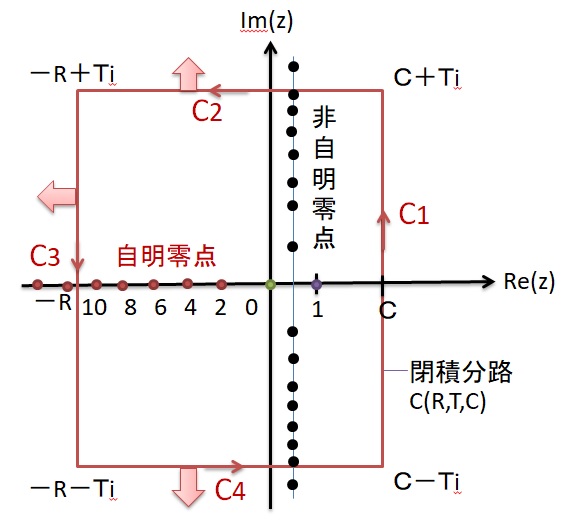
となります。この複素積分を閉曲線C(c,T,R）

　C(c,T,R)＝C_{1[c－Ti、c＋Ti]}＋C_{2[c+Ti、－R＋Ti]}＋C_{3[－R＋Ti、－R －Ti]}＋C_{4[－R－Ti、c－Ti]}

に拡張すると、

　lim_[R,T→∞]∫_C2 f_x(s)ds＝lim_[R,T→∞]∫_C3 f_x(s)ds＝lim_[R,T→∞]∫_C4 f_x(s)ds＝0

となるので、

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds

　　　　＝－1/2πi・lim_[R,T→∞]∫_C(c,T,R）f_x(s)ds

となります。閉曲線内に含まれるf_x(s)の極の留数を計算すれば、Ψ^*(x)を求めることができます。

＜マンゴルトの明示公式＞

チェビシェフの素数pの階段関数

　Ψ^*(x)＝Σ[n≦x]Λ(n)＝Σ[p^m≦x] log(p)

に関して

　Ψ^*(x)＝x－1/2・log(1－x^－2)－log 2π－Σ’_ρ∊Z0x^ρ/ρ

がなりたつ。ここでZ₀＝｛ｓ｜ζ(s)＝0なる非自明な零点｝である。マンゴルトの明示公式は、素数の分布を表す階段関数Ψ^*(x)がゼ－タ関数の非自明な零点の和を含むｘの解析関数によって書かれているという不思議な公式です。

閉曲線内の

　f_x(s)＝ζ'(s)/ζ(s)・x^s/s

の零点は、ρ＝1、－2n、0、ρ_iの4種類あります。

まずζ'(s)/ζ(s)の留数を考えます。

　ζ(s)～1/(s－1)+・・

　ζ'(s)～－1/(s－1)²+・・

　ζ'(s)/ζ(s)～－1/(s－1)+・・

なので、極をρとすると、位数Ord(ζ,ρ)について

　Res(ζ’/ζ,ρ)＝Ord(ζ,ρ)

が成り立ちます。偏角の原理より、留数は

　Res(ζ'(s)/ζ(s)・x^s/s,ρ)＝Ord(ζ,ρ) x^ρ/ρ

となります。

1）s＝1の留数

　Ord(ζ,1)＝－1となります。

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝1)＝Ord(ζ,1) x¹/1＝－x

2）s＝－2nの留数

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝－2n)＝Ord(ζ,1) x^－2n/(－2n)

R→∞でN→∞となるので

　－lim_[N→∞]Σ_n＝1～N x^－2n/(－2n)＝1/2・log(1－x^－2)

3）s＝0の留数

　　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝0)＝ζ'(0)/ζ(0)＝log(2π)

　　ζ(0)＝－1/2、ζ’(0)＝－1/2・log(2π)

4）ｓの非自明な零点ρ_iの留数

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝ρ_i)＝Ord(ζ,ρ_i) x^ρi /ρ_i

T→∞でN→∞となるので

　lim_[N→∞]Σ_i＝1～N Ord(ζ,ρ_i) x^ρi /ρ_i＝Σ’_ρ∊Z0 x^ρ /ρ

Σ’_ρ∊Z0は非自明な零点ρでの位数がｍの場合ｍ回和をとると言う意味です。

以上から、マンゴルトの明示公式

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds

　　　　＝－1/2πi・lim_[R,T→∞]∫_C(c,T,R）f_x(s)ds

　　　　＝－1/2πi・2πi・（－x＋1/2・log(1－x^－2)＋log 2π＋Σ’_ρ∊Z0 x^ρ /ρ）

　　　＝x－1/2・log(1－x^－2)－log 2π－Σ’_ρ∊Z0 x^ρ /ρ

が成り立ちます。

偏角原理とは、z=z₀でm位の特異点をもちそれ以外で正則な関数f(z)に関して

　Res(f’/f,z₀)＝Ord(f,z₀)＝m

が成り立つ定理です。f(z)は、z=z₀で特異点をもたない正則関数g(z)を用いて

　f(z)＝(z－z₀)^m・g(z)

と書けます。このとき、

　f'(z) /f(z)＝[m(z－z₀)^m－1・g(z)＋(z－z₀)^m・g'(z)]/ (z－z₀)^m・g(z)

　　　　　＝m/(z－z₀)＋g'(z)/ g(z)

なので、f'(z) /f(z)はz＝z₀で1位の極を持つことがわかり

　Res(f’/f,z₀) ＝m＝Ord(f,z₀)

が成り立ちます。