1749年にオイラ－は

• Z＝1＋1＋1＋1＋1＋・・・＝－1/2

という不思議な級数の値を求めました。時々皆さんも目にすることがあると思います。今日はこの式の意味する所を考えてみます。

まず関数

• f₀(x)＝1/(1＋x)、f₀(1)＝1/2

を考えます。この関数を展開すると

• f(x)＝1－x＋x²－x³＋x⁴－x⁵＋・・・　for　｜x｜＜1

と表すことができます。但しこの関数はｘ＝1では定義されていません。

形式的にｘ＝1を代入し、その値をYとします。

• f(1)＝1－1＋1－1＋1－1＋・・・＝Y

となります。元の関数をｘのｎ次までの展開した関数を

　　f_n(x)=Σ_ｋ＝0～n (－x)^k→　1/(1＋x)　x≠1　as  n→∞

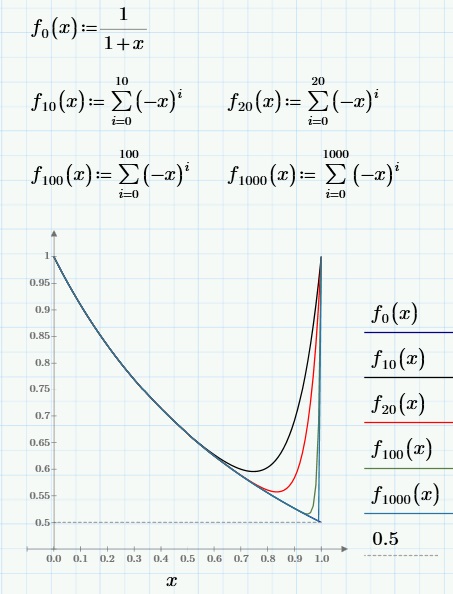
と定義します。グラフにｎ＝10，20、100、1000の場合の関数形を表示します。

nが無限大の極限で、関数f_n(x)はｘ＜1で関数1/(1＋x)に一致することが分かります。つまりｘ→1の片側極限で

• lim x→1 f(x)＝1/2

が成り立っています。そこで

• f(1)＝1/2

と定義すれば、関数f(x)は0≦ｘ≦1で1/(1+x)に一致します。これは

• 　Y＝1－1＋1－1＋1－1＋・・・＝1/2

を示しています。ZもYと同じような意味で値を持つと考えます。そうすると

　2Z＝   2＋   2＋   2＋　 2＋・・・

　 Z＝1＋1＋1＋1＋1＋1＋1＋1＋・・・

を辺々引くと

　Z＝2Z－Z＝－1＋1－1＋1－1＋1－1＋・・・

が得られます。両辺に1を加えて

　1＋Z＝1－1＋1－1＋1－1＋1－1＋・・・＝Y＝1/2

なので、関数の極限の意味で

　Z＝1/2－1＝－1/2

となっている可能性があります。

実はこの話はゼ－タ関数

　ζ(s)＝1＋1/2^s＋1/3^s＋1/4^s＋1/5^s＋・・・

のs→0での極限値が－1/2であることにつながっています。s＝0での値を

　ζ(0)＝－1/2

と定義すると、ゼ－タ関数はs＝0で滑らかな関数になります。これは

　Z＝1＋1＋1＋1＋1＋・・・＝－1/2

を表しています。