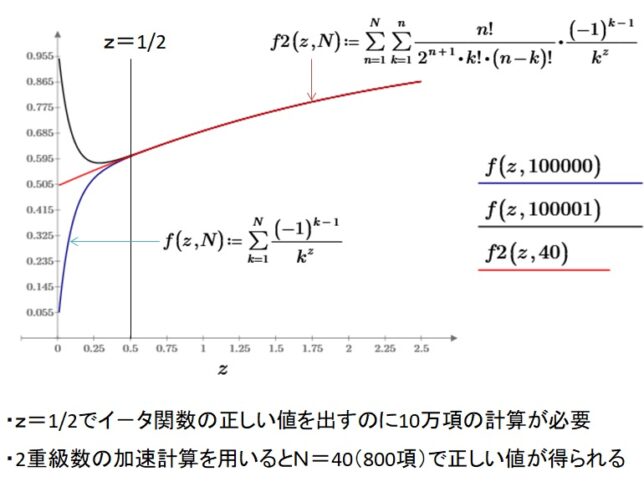
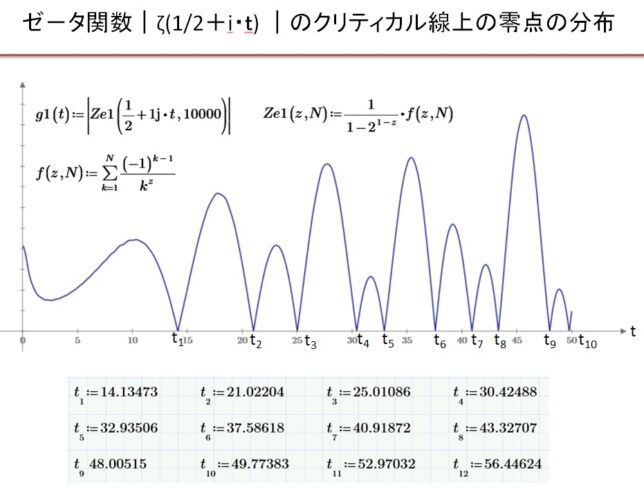
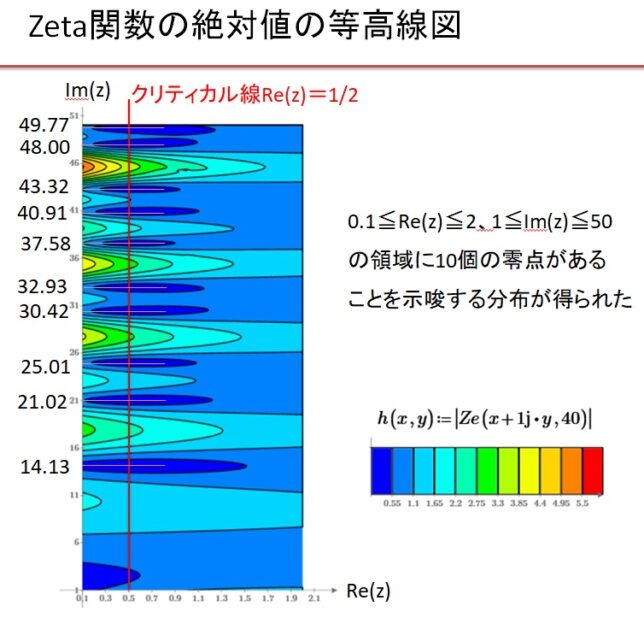
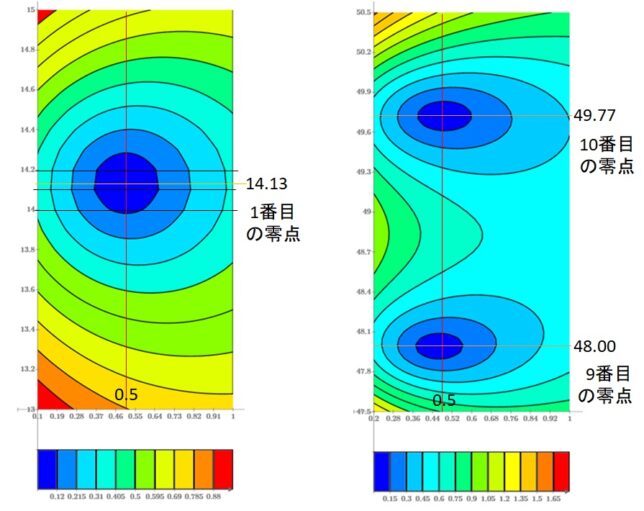
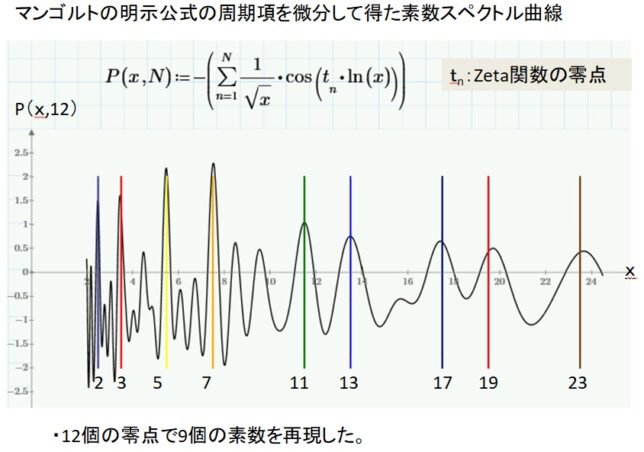
＜テータ関数の変換公式＞

ｓ＞0のとき

　θ(s)＝Σ_{n＝－∞～∞}exp(－πsn²)

に対して、

　θ(1/s)＝√s・θ(s)

が成り立つ。

[証明]　関数f(t)を

　f(t)＝exp(－πst²)

とおくと、

　θ(n)＝Σ_{n＝－∞～∞}f(n)

である。f(t)のフーリエ変換をF(m)とすると

　F(m)＝∫_{[－∞、∞]} exp(－πst²)e^－i2πmt dt

である。これをｍで一回微分すると

　d F(m)/dm＝∫_{[－∞、∞]} exp(－πst²) (－i2πt)e^－i2πmt dt

　　　　　  ＝i/s・∫_{[－∞、∞]} (－2πst)exp(－πst²) e^－i2πmt dt

                    ＝i/s・∫_{[－∞、∞]} (d/dt)exp(－πst²) e^－i2πmt dt

                  ＝i/s・[exp(－πst²) e^－i2πmt]t=_－∞、∞－i/s∫_{[－∞、∞]} exp(－πst²) (－i2πm) e^－i2πmt dt

　　　　   ＝－2πm/s・∫_{[－∞、∞]} exp(－πst²) e^－i2πmt dt

　　　　   ＝－2πm/s・F(m)

となる。微分方程式を解くと

　[logF(m)]’＝F’(m)/ F(m)＝－2πm/s
    logF(m)＝－πm²/s

を解いて、
   F(m)＝F(0)exp(－πm²/s)

が得られる。

　F(0)＝∫_{[－∞、∞]} exp(－πst²) dt

ここで、u＝√(πs)・t　と置くと

　F(0)＝1/√(πs)∫_{[－∞、∞]} exp(－u²) du

　　　＝1/√(πs)・√π　＝1/√s

従って、フ－リエ変換後の関数は

　　F(m)＝1/√s ・exp(－πm²/s)

となる。ここで

f(t)＝exp(－πst²)　は[－∞、∞]区間上の連続関数であるから、Poissonの和公式より

　Σ_n f(n)＝Σ_n F(n)

すなわち

　Σ_n exp(－πsn²)＝Σ_n 1/√s ・exp(－πn²/s)

が成り立つ。いま、θ(s)＝Σ_{n＝－∞～∞}exp(－πsn²)　より

　θ(s)＝1/√s ・θ(1/s)

が成り立つことが示された。

 

[補題]　正の実数xに対して、

　Σ_n exp[－π(n＋α)²/x]＝√x Σ_n exp[－πn²x＋ i2πnα]

が成り立つ。

・α＝0を代入すると、θ(1/x)＝√x ・θ(x)　が成り立つ。

[証明]　

  f_αx(y)＝exp[－π(y＋α)²/x]

とおいて、

  Σ_n f_αx(y)＝√x Σ_n exp[－πn²x＋ i2πnα]

を示す。Poissonの和公式より

　Σ_n f_αx(n)＝Σ_n∫_{[－∞、∞]} f_αx(y) e^－i2πny dy

＝Σ_n ∫_{[－∞、∞]} exp[－π(y＋α)²/x] e^－i2πny dy

ここで、y+α＝xuとおくと、

  Σ_n f_αx(n)＝Σ_n∫_{[－∞、∞]} exp[－πxu²] e^{－i2πn(xu－α)} dy

                 ＝Σ_n e^i2πnα∫_{[－∞、∞]} exp[－πxu²] e^－i2πnxu xdu

ここで

    －πxu²－i2πnxu＝－πx(u²＋i2nu)＝－πx(u＋in) ²－πxn ²

であるから、

     Σ_nf_αx(n)＝xΣ_ne^i2πnαexp[－πxn ²]∫_{[－∞、∞]} exp[－πx(u＋in)²] du　　

　　　　　  ＝xΣ_ne^i2πnαexp[－πxn ²]・lim_N→∞ I(N)

ここで
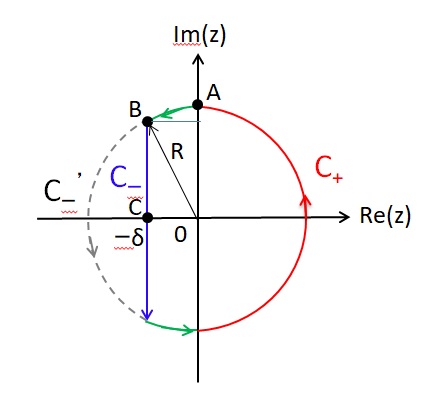
    I(N)＝∫_[－N、N] exp[－πx(u＋in)²] du＝∫_Aexp[－πx(u＋in)²] du　　

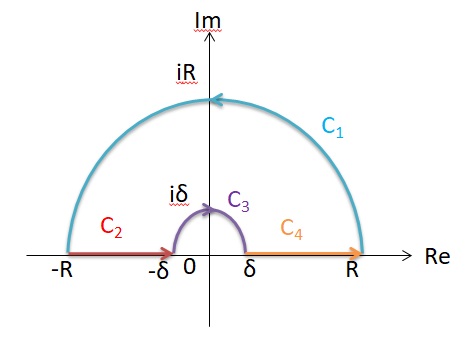
とした。この積分の経路は複素平面で、

  A：z＝u＋in（－N≦u≦N）

である。コーシ－の定理より、非積分関数は正則関数なので、経路A上の複素積分を以下のB→C→Dに変えることができる。

   I(N)＝∫_B→C→D exp[－πx(z)²] dz　　

において

　B：z＝－N+it、0≦t≦n

　C：z＝t、－N≦t≦N

　D：z＝N+it、0≦t≦n

経路Bでの積分は

　I_B(N)＝∫_[n、0] exp[－πx(－N＋it)²] dt　　

          ＝－exp[－πxN²]∫_[0、n] exp[(1－it/N)²] dt　

ここでt’＝t/N　とおくと、

  I_B(N)＝∫_[0、n] exp[(1－it/N)²] dt

       ＝1/N・∫_[0、n/N] exp[(1－it’)²] dt’　→ 0　as　N→∞

となり、N→∞での積分値はゼロになる。

同様に経路Dでの積分は

   I_D(N)＝∫_[0、N] exp[－πx(N＋it)²] dt

          ＝1/N・∫_[0、n/N] exp[(1＋it’)²] dt’　→ 0　as　N→∞

となり、N→∞での積分値はゼロになる。経路Cでの積分は

   I_C(N)＝∫_[－N、N] exp[－πxt²] dt　　

　　　＝1/√(πx) ・∫_[－N、N] exp[－t²] dt　→　√π/√(πx)＝1/√x　as　N→∞

となり、N→∞での積分値は1/√xとなる。

従って

　lim_N→∞ I(N)＝lim_N→∞｛I_B(N)＋I_C(N)＋I_D(N)｝＝1/√x　

を得る。結局

  Σ_n f_αx(n)＝x Σ_ne^i2πnαexp[－πxn ²]・lim_N→∞ I(N)

　　　　＝x Σ_ne^i2πnαexp[－πxn ²] 1/√x
              ＝√x・Σ_nexp[－πxn ²＋i2πnα]

が成り立つことが示された。

＜Poissonの和公式＞

[－∞、∞]区間上の任意の連続関数f(x)とそれをフーリエ変換した関数

　F(n)＝∫_{[－∞、∞]} f(t)e^－i2πnt dt

に対して、

　Σ_{n＝－∞～∞} f(n)＝Σ_{n＝－∞～∞} F(n)

が成り立つ。

[証明]　 連続関数f(t)に対して

　g(t)＝Σ_{n＝－∞～∞}f(n+t)

を定義する。

　g(0)＝Σ_{n＝－∞～∞}f(n)

であり、g(t)は

　g(t+1)＝g(t)

なる周期性を持つので、フ－リエ級数展開

　g(t)＝Σ_{n＝－∞～∞}c_n e^i2πnt

ができる。t=0のとき

　g(0)＝Σ_{n＝－∞～∞}c_n

が成り立つ。一方、

　F(m)＝Σ_{n＝－∞～∞}∫_[n、n+1] f(t)e^－i2πmt dt

　　　＝Σ_{n＝－∞～∞}∫_[0、1] f(t+n)e^{－i2πm(t+n)} dt

　　　＝∫_[0、1] [Σ_{n＝－∞～∞}f(t+n)] e^－i2πmt dt

　　　＝∫_[0、1] g(t) e^－i2πmt dt

　　　＝∫_[0、1] [Σ_{n＝－∞～∞}c_n e^i2πnt] e^－i2πmt dt

　　　＝Σ_{n＝－∞～∞}c_n・[∫_[0、1] e^i2π(n－m)t dt]

　　　＝Σ_{n＝－∞～∞}c_n・δ_nm

　　　＝c_m

従って

　g(0)＝Σ_{n＝－∞～∞}f(n)＝Σ_{n＝－∞～∞} F(m)

が成り立つ。

 

ディリクレ積分

　∫_[0,∞] sin(x) /x dx＝π/2　

を複素積分

　∫_C e^iz /z dz＝0

で求めます。

閉積分経路Cを

　C＝C₁＋C₂＋C₃＋C₄

に分けます。ここで

　C₁：z＝Re^iθ0≦θ≦π

　C₂：z＝x　–R≦x≦－δ

　C₃：z＝δe^iθ0≦θ≦π

　C₄：z＝x　δ≦x≦R

とします。閉積分経路C内にz=0の極は含まれないので、Cでの積分はコーシ－の定理よりゼロになります。

（1）C₁の積分

　0≦sinθ≦1　かつ　2θ/π≦sinθ（0≦θ≦π）、

ですから、

　｜exp(iRe^iθ)｜＝｜exp{iR(cosθ+ i sinθ)}｜

　　　　　　　＝｜exp{iRcosθ}・exp{－R sinθ)}]｜

　　　　　　　＝e^{－R sinθ}

　　　　　　　≦e^－R2θ/π

従って

　｜∫_C1 e^iz /z dz｜＝｜∫_[0，π]  exp(iRe^iθ) /Re^iθ ・iRe^iθdθ｜

　　　　　　　　 ≦∫_[0，π] e^－R2θ/πdθ

　　　　　　　　 ＝－π/2R・[e^－R2θ/π] _θ＝0，π

＝π/2R・(1－e^－2R)　→　0　as　R→∞

C₁の積分はRが無限大になるとゼロになります。

（2）C₂の積分

ここで　x’＝‐xに置き換えると

　∫_C2 e^iz /z dz＝∫_[R，δ] e^‐ix’ /x’ dx’＝－∫_[δ、R] e^‐ix’ /x’ dx’

となります。

（3）C₃の積分

　　∫_C3 e^iz /z dz＝∫_[π，0]  exp(iδe^iθ) /δe^iθ ・iδe^iθdθ

　＝i∫_[π，0]  {1+(iδe^iθ)+O(δ²)｝dθ

　→　i∫_[π，0] dθ＝－iπ　as　δ→0

（4）C₄の積分

　∫_C3 e^iz /z dz＝∫_[δ、R] e^ix /x dx

となります。以上より

0＝∫_C1 e^iz /z dz＋∫_C2 e^iz /z dz＋∫_C3 e^iz /z dz＋∫_C4 e^iz /z dz

　　＝∫_CRe^iz /z dz－∫_[δ、R] e‐^ix /x dx＋∫_[δ、R] e^ix /x dx－iπ

　　＝∫_CRe^iz /z dz ＋∫_[δ、R](e^ix－e^‐ix) /x dx－iπ

　　＝∫_CRe^iz /z dz ＋2i∫_[δ、R]sin(x) /x dx－iπ

ここで　δ→0かつR→∞　とすると

　2i∫_[0、∞]sin(x) /x dx－iπ＝0

すなわち

　∫_[0、∞]sin(x) /x dx＝π/2

が得られます。複素積分を用いると簡単にディリクレ積分の値が求められました。

ペーター・グスタフ・ディリクレ（Peter Gustav Dirichlet, 1805年～1859年）はフランス生まれのドイツ人数学者です。ディリクレは現代的な関数概念（写像）を与えたことで知られています。家族の名前Dirichletは祖父がベルギ-のリシュレの街の出身だったことに由来しています。ペータ－はガウスの「整数論」を持ってフランスへ行き、パリ大学などで、フ－リエ（指導教官）、ラプラス、ルジャンドルらから数論と解析学を学びます。ペータ－は22歳の時にドイツに戻り、10年間ベルリン大学に滞在し、レベッカ・メンデルスゾーンと結婚します。妻のお兄さんは有名な作曲家で、彼の家は絶えず賑やかだったそうです。ディリクレは1855年からガウスの後継として、ゲッティンゲン大学で教授を務めます。友達の数学者にカ－ル・グスタフ・ヤコビがいます。彼の教え子たちにはアイゼンシュタイン、リーマン、クロネッカー、リプシッツがいます。友人の数学者リヒャルト・デ‐デキントが彼の研究結果をまとめて『整数論講義』を出版しました。ディリクレの名前が付けられた定理は、数論や解析学で数多く出てきます。ディリクレの積分定理は師匠のフーリエ変換の数学的基礎づけを行うためのものです。

＜ディリクレの積分定理＞

区分的に滑らかな関数f(x)に関して

　Lim _λ→∞∫_[－a,－a] f(x)sin(λx)／x dx＝π/2・[f(+0)＋f(－0)]

が成り立つ。ここで

　f(+0)＝Lim _x→0 f(x)  for　x＞0

　f(－0)＝Lim _x→0 f(x)  for　x＜0

のことです。f(x)がx＝0で連続ならば、

　Lim _λ→∞∫_[－a,－a] f(x)sin(λx)／x dx＝π・f(0)

となります。「区分的に滑らか」とは積分区間で有限個の有限な不連続点があり、その間は1回微分可能であることを意味しています。

[証明]

I(λ)＝∫_[b,ｃ] f(x)sin(λx) dx

とおくと、

　Lim _λ→∞ I(λ)＝0　　・・・（1）

が成り立ちます。（1）式は後で証明します。一方

　∫_[0,∞] sin(λx) /x dx＝π/2　（λ＞0）　・・・（2）

が成り立ちます。この積分をディリクレ積分と呼びます。ディリクレ積分は収束しますが、絶対収束しない積分として有名です。（2）式も後で証明します。

I(λ)において、f(x)→{f(x)－f(+0)}／x と置き換えると、

　　f’(0)＝Lim _x→0{f(x)－f(+0)}／x

は存在しているので、

　∫_[0,a] {f(x)－f(+0)}／x ・sin(λx) dx＋∫_[－a,0] {f(x)－f(+0)}／x ・sin(λx) dx　→0　λ→∞

が成り立ちます。すなわち

　∫_[－a,a] f(x) sin(λx)／x dx＝f(+0)∫_[0,a] sin(λx)／x dx＋f(－0)∫_[－a,0] sin(λx)／x dx

x’＝－x　とおくと

　∫_[－a,0] sin(λx)／x dx＝－∫_[＋a,0] sin(λx’)／x’ dx’＝∫_[0,a] sin(λx)／x dx

であるから、

　∫_[－a,a] f(x) sin(λx)／x dx＝[f(+0)＋f(－0)]・∫_[0,a] sin(λx)／x dx

となります。a→∞をとると、（2）式より

　∫_[－∞,∞] f(x) sin(λx)／x dx＝[f(+0)＋f(－0)]・π/2

が得られます。

f(x)＝1のとき、x’＝λxとおくと

　∫_[－∞,∞] sin(λx)／x dx＝∫_[－∞,∞] sin(x’)／x’ dx’＝π/2

が成り立ちます。

次に（1）式の証明を行います。x＝y＋π/λ　とします。

　　Sin(λ(y＋π/λ))＝sin(λy＋π)＝－sin(λy)

　I(λ)＝－∫_{[b－π/λ、c－π/λ]} f(y＋π/λ) sin(λy)dy・・・（3）

となります。

　I(λ)＝∫_[b,c] f(x)sin(λx) dx・・・（4）

(3)＋(4)を行うと、積分区間を

　　[b －π/λ、c]＝[b－π/λ、b]＋[b、c－π/λ]＋[c－π/λ、c]

に分割できるので、

　2 I(λ)＝－∫_{[b－π/λ、b]} f(x＋π/λ)sin(λx) dx＋∫_{[b、c－π/λ]} [ f(x)－f(x＋π/λ)]sin(λx) dx

　　　　　＋∫_{[c－π/λ、c]} f(x)sin(λx) dx

となります。ワイエルシュトラスの最大値定理より、閉区間[b、c]において、最大値M＞0が存在して

　｜f(x) sin(λx)｜≦｜f(x)｜≦M　となるので、

　2｜I(λ)｜≦2Mπ/λ＋∫_{[b、c－π/λ]} ｜f(x)－f(x＋π/λ)｜dx　＜2ε

となります。任意のε＞0に対して、λ＞0が存在して、

　　2Mπ/λ＜ε　　かつ　　｜f(x)－f(x＋π/λ)｜＜ε/(c－b)

が成り立ちます。従って

　　lim_λ→∞｜I(λ)｜＝0　

が示されました。

＜フーリエの積分定理＞

区分的に滑らかな関数f(t)に対して

　　F(ω)＝∫_{[－∞、∞]}f(t)e^－iωtdt

が存在し、

　　1/2π・∫_{[－∞、∞]} F(ω) e^－iωtdω＝1/2・[f(t＋0)＋f(t－0)]

が成り立つ。

証明)　ディリクレの積分定理より、区分的に滑らかな関数f(x)に関して

　Lim_λ→∞∫_[－a,－a] f(τ)sin(λτ)／τ dτ＝π/2・[f(+0)＋f(－0)]

が成り立ちます。いま、f(τ)をf(τ+t)と置き換え、a→∞とすると

　Lim_λ→∞∫_{[－∞,－∞]} f(τ+ｔ)sin(λτ)／τ dτ＝π/2・[f(t+0)＋f(t－0)]

t’＝τ+ｔと変数変換すると

　左辺＝Lim_λ→∞∫_{[－∞,－∞]} f(t’)sin(λ(t’－t))／(t’－t) dt’

となります。

　∫_[0,λ] cosω (t’－t)dω＝[sin(ω(t’－t))／(t’－t)]_ω＝0、λ＝sin(λ(t’－t))／(t’－t)

ですから、これを代入すると

　左辺＝Lim_λ→∞∫_{[－∞,－∞]} f(t’) [∫_[0,λ] cosω (t’－t)dω] dt’

となる。ここで

　cosω (t’－t)＝1/2(e^{iω (t’－t)}＋e ^{－iω (t’－t)})

です。ω’＝－ωと置くと

　∫_[0,∞] e^{iω (t’－t)} dω＝－∫_[0,－∞] e^{－iω’ (t’－t)} dω’＝ ∫_[－∞,0] e^{－iω (t’－t)} dω

となります。

左辺＝1/2∫_{[－∞,－∞]} f(t’) [∫_[0,∞] e^{iω (t’－t)}dω＋∫_[－∞,0] e^{－iω (t’－t)}dω] dt’

　　＝1/2∫_{[－∞,－∞]} f(t’) [∫_[－∞,∞] e^{－iω (t’－t)}dω] dt’

　　＝1/2∫_{[－∞,－∞]} [∫_[－∞,∞] f(t’) e^－iωt’ dt’ ] e^iωt dω

が得られます。よって

　F(ω)＝∫_[－∞,∞] f(t) e^－iωt dt

とおくと、

　1/2π・∫_{[－∞,－∞]} F(ω)e^iωt dω ＝1/2・[f(t+0)＋f(t－0)]

が示されました。

ディリクレ積分

　　∫_[0,∞] sin(λx) /x dx＝π/2　（λ＞0）　・・・（2）

は収束しますが、

　∫_[0,∞] ｜sin(x) /x｜dx＝Σ_k=1～∞∫_{[(k－1)π、kπ]} ｜sin(x)｜/x dx

　　　　　　　　　　　≧Σ_k=1～∞∫_{[(k－1)π、kπ]} ｜sin(x)｜/kπ dx

　　　　　　　　　　　＝1/π・Σ_k=1～∞1/k∫_[0、π] sin(x)dx

　　　　　　　　　　　＝2/π・Σ_k=1～∞1/k　＝∞

によって絶対収束しません。

命題1　

　∫_[0、∞] e^－axsin(x) /x dx＝π/2－tan^－1(a)　a＞0

が成り立つ。

部分積分をすると、

I(a)＝∫_[0、∞] e^－axsin(x) dx＝－[e^－axcos(x)]_x＝0～∞＋∫_[0、∞] (－a)e^－axcos(x) dx＝

　　　＝1－a｛[e^－axsin(x)] _x＝0～∞－(－a)∫_[0、∞] e^－axsin(x) dx｝

　　　＝1－a²I(a)

　I(a)＝1/(1＋a²)

となります。

　　∫_[∞、a’] I(a)da＝∫_[∞、a’]∫_[0、∞] e^－axsin(x) dx da

　＝∫_[0、∞] [∫_[∞、a’] e^－ax da] e^－ax da sin(x) dx

ここで

　　∫_[∞、a’] e^－ax da＝－1/x・[e^－ax]_{a＝∞～a’}＝ －1/x・e^－a’x

であるから、

　∫_[0、a’] I(a)da＝－∫_[0、∞] e^－a’x sin(x)/x dx

一方、

∫_[∞、a’] I(a)da＝∫_[∞、a’] 1/(1＋a²)da

a=tanθ-とおくと、1/(1+tan²θ)=cos²θ、da=1/ cos²θdθ

a：∞→a’、 θ：π/2→tan^－1(a’) より

∫_[∞、a’] I(a)da＝∫_{[π/2、tan－1(a’)]} 1da＝tan^－1(a’)－π/2＝－∫_[0、∞] e^－a’x sin(x)/x dx

である。従って

　∫_[0、∞] e^－ax sin(x)/x dx＝π/2－tan^－1(a)

が示された。

上式でa=0のとき

　I(0)＝∫_[0,∞] sin(x) /x dx＝π/2　

が成り立ちます。上式は複素積分で示すこともできます。

ゼ－タ関数は

　ζ(z)＝∑_k=1～∞1/k^z＝1＋1/2^z＋1/3^z＋1/4^z＋・・・　　　Re(z)＞1

という複素関数です。ゼ－タ関数の零点とは、ζ(z)＝0となるｚのことです。今回はゼ－タ関数の零点を計算してみました。前回、ゼ－タ関数は

　ζ(z)＝∏_p(1/[1－1/p^z])＝1／[1－1/2^z]・[1－1/3^z]・[1－1/5^z]・[1－1/7^z]・・・

のように素数の積で表示できることを示しました。このことが示唆するように、ゼ－タ関数の零点と素数には密接な関係があることが知られています。

前回、イ－タ関数η(z)　（前回はη(z)をL(z)と書きました。）

　η(z)＝∑_k=1～∞(－1)^k－1/k^z＝1－1/2^z＋1/3^z－1/4^z＋1/5^z－1/7^z＋・・・          Re(z)＞0

を使うと、ゼ－タ関数

　ζ(z)＝η(z)/(1－2^1－z)　　Re(z)＞0　ｚ≠1

の定義域は、Re(z)＞0に拡大できることを示しました。ゼ－タ関数は、ガンマ関数を用いて表示することでRe(z)＜0にも拡大できます。ゼ－タ関数の零点には、ｚ＝－2、－4、－6・・・・に自明な零点があることが分かっています。1859年にリ－マンはゼ－タ関数の非自明な零点はRe(z)＝1/2の線上に分布すると予想しました。今回は

　ζ(z)＝η(z)/(1－2^1－z)＝0

を満たす非自明な零点の分布を調べて見ました。問題は、無限和を有限和で置き換えると、級数の収束が遅いので、誤差が大きくなってしまうことです。私のパソコンでは、10万項の級数を計算しても、Re(z)＝1/2の線上の零点の虚数座標を有効数字4桁の精度（t₁＝14.13）でしか求められませんでした。そこでクノップ変換を行い級数の収束性を高めました。　N＝40（40×40/2＝800項）の計算で零点を有効数字7桁の精度（t₁＝14.13473）で求めることができました。マンゴルトの明示公式の周期項を微分して得た素数スペクトル曲線に12個の零点を入れて9個の素数を再現しました。

クノップ変換では。収束が遅い級数に「1に収束する級数」を挿入して和の順番を変えることで、級数の収束性を高めます。パラメータｑの値を変えることで、収束速度と収束領域が変わります。

関数b(k,N)はNが無限大になると1になりますが、Nが有限だと、ｋがN/2より大きい所では1より小さくなります。　コンラッド・クノップ(1882～1957)は無限級数の収束を研究したドイツ人の数学者です。

 

[12]素数定理の証明手順のまとめ

[０]関数の定義　P；素数の集合

・リーマンのゼ－タ－関数：ζ(s)＝Σ_{[n＝1～∞]} 1/n^s、Re(s)＞1

　（nに関する無限級数）

・ファイ関数：Φ(s)＝Σ_[p∊P] log(p)／p^s、Re(s)＞1

　（すべての素数に関する和をとる）

・チェビシェフのシータ関数：θ(x)＝Σ_[p≦x] log(p)

  （X以下の素数pに関する和をとる）

・素数の個数関数：π(x)＝Σ_[p≦x]1

[Ⅰ]命題1　Re(s)＞1、ζ(s)＝Π_[p∊P] [1／(1－1/p^s)]　オイラ－積表示の存在

（1）Re(s)＞1でζ(s)のディリクレ級数表示は収束する。

（2）ζ(s)のディリクレ級数表示はオイラ－積表示に一致する。

（3）Re(s)＞1でζ(s)のオイラ－積表示は収束する。

（4）ζ(s)は、s＞0（s≠1）に拡張することができる。

[Ⅱ] 命題2　ζ(s)－1/(ｓ－1)はRe(s)＞0で正則である。

（1）∫_[1,∞]1/x^s dx＝1/(s‐1)　for　s＞1

（2）s∫_[n,x] 1/t^s+1 dt＝1/n^s－1/x^s

（3）｜t^s+1｜＝t^Re(s)+1

（4）ζ(s)－1/(ｓ－1)≦｜s｜ζ( Re(s)+1) for　s＞1　

[Ⅲ] 命題3　Φ(s)－1/(ｓ－1)はRe(s)≧1で正則である。

（1）ζ’(s)/ζ(s) ＋1/(s－1)　はRe(s)≧1で正則である。

（2）Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)＋1/(s‐1)]－Σ[p] log(p)／p^s(p^s‐1) 　を示す。

（3）右辺2項目Σ[p] log(p)／p^s(p^s‐1)はRe(s)＞1/2で正則である。

（4）Re(s)＝1でζ(s)＝0なる零点が存在しない。

[Ⅳ] 命題4　θ(x)＝Ｏ(x)　i.e.　∃ｋ＞0　｜θ(x)｜≦ｋx

（1）2nlog2≧θ(2n)－θ(n)

（2）2^ｍ+1・log2＞θ(2^m)

  (3) θ(x) ≦4log2・x

[Ⅴ] 命題5　∫_[1，∞] [θ(x)－x]／x² dxは収束する。

・[Ⅲ] 、[Ⅳ]、[定理A]を用いて証明する。

（1）Φ(s)＝s∫_[1，∞] θ(x)／x^ｓ+1dx、Re(s)＞1

（2）f(t)＝θ(e^t)e^－t－1　（t≧0）は有界、g(z)＝∫_[0，∞] f(t)exp[－zt] dtが存在する

（3）g(z)＝Φ(z+1)／(z+1)－1/z　　Re(z)＞0

（4）g(z)はRe(z)≧0で正則

（5）g(0)＝∫_[0，∞] f(t) dt＝∫_[1，∞] [θ(x)－x]／x² dx　が収束する。

[Ⅵ] 命題6　θ(x)～x　i.e.　lim_[x→∞] θ(x)/x＝1

・任意のε＞0、∃x＞0　1－ε＜θ(x)/x＜1＋εを示す。

・背理法を用いて矛盾を示す。任意の正数ｘに対して、∃ε＞0

（1）1＋ε≦θ(x)/x　は矛盾を生じるので、θ(x)/x＜1＋ε　by [Ⅴ]

（2）θ(x)/x≦1－ε　は矛盾を生じるので、1－ε＜θ(x)/x 　by [Ⅴ]

[Ⅶ] 素数定理　Lim _[x→∞] π(x) logx／x＝1

（1）1←θ(x)/x≦π(x)log(x)/x　by [Ⅵ]

（2）π(x)log(x)/x≦1/(1－ε)・θ(x)/x＋log(x)/x^ε→1/(1－ε)　→1

[定理A]　Newmanの解析定理

t≧0で有界かつ可積分な関数f(t)に対して、

g(z)＝∫_[0，∞] f(t)exp[－zt] dt　Re(z)＞0

がRe(z)≧0で正則であれば、

　g(0)＝∫_[0，∞] f(t) dt

が存在する。つまり正則関数

　g_T(z)＝∫_[0，T] f(t)exp[－zt] dt

に対して、

　lim_[T→∞]g_T(0)＝g(0)

が存在する。

[定理A]　Newmanの解析定理の証明手順

（1）g(0)－g_T(0)＝1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz

（2）A＝｜g(0)－g_T(0)｜＝｜1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz｜

　　　≦A₊＋A_－≦A₊＋A_－1＋A_－2 → 2B/R（T→∞）→ 0 （R→∞）

（3）A₊≦B/R、Re(z)＞0　

（4）A_－1＝｜1/2πi・∫_C－g_T(z)e^zT(1＋z²/R²)／z dz｜≦B/R　

（5）A_－2＝｜1/2πi・∫_C－g(z)e^zT(1＋z²/R²)／z dz｜→ 0

[Ⅷ]　Newmanの解析定理の証明

（1）g(0)－g_T(0)＝1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz を示します。

コ－シ－の積分公式より、領域Dで正則な複素関数f(z)のD内の閉曲線C上の積分に関して、

閉曲線Cで囲まれた領域の点αにおいて

• f(α)＝1/2πi・∫_C f(z)／(z－α) dz

が成り立つ。閉曲線Cの半径R＞0として、

• f(z)＝[g(z)－g_T(z)]e^zT(1＋z²/R²)

を考えると、f(z)は以下で定義される領域Dで正則であることが分かります。

任意の閉曲線C上のg_T(z)の積分は、∫_C e^－ztdz＝0より

• ∫_C g_T(z)dz＝∫_C (∫_[0,T]f(t)e^－ztdt)dz＝∫_[0,T] f(t) (∫_C e^－ztdz)dt＝0

です。モレラの定理から、g_T(z)は任意の閉曲線C内で正則です。解析定理の前提より、g(z)はRe(z)≧0で正則なので、Re(z)＝0上の任意の点z＝it（－∞≦t≦∞）でテ－ラ－展開でき、その収束円内のzでも正則です。従って、十分大きなR＞0と十分小さなδ＞0において、「｜z｜≦R　かつ－δ≦Re(z)」となる領域Dの境界線を閉曲線Cとすると、閉曲線Cの内部領域Dでg(z)とg_T(z)は正則です。e^zT(1＋z²/R²)も正則なので、f(z)は正則関数となり、

コ－シ－の積分公式を適用できます。いまz＝0で

• f(0)＝g(0)－g_T(0)

です。α＝0として、コ－シ－の積分公式を適用すると

• f(0)＝g(0)－g_T(0)＝1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz

が成り立ちます。

（2）A＝｜g(0)－g_T(0)｜＝｜1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz｜

　　　≦A₊＋A_－≦A₊＋A_－1＋A_－2 → 2B/R（T→∞）→ 0 （R→∞）

を示します。そのために、積分路を

• C＝C₊ (Re(z)＞0)＋C_－(Re(z)＜0)

に分け、

　A₊＝｜1/2πi・∫_C+ [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz｜

　A_－＝｜1/2πi・∫_C－[g(z)－g_T(z)] e^zT(1＋z²/R²)／z dz｜≦ A_－1＋A_－2

とします。ここで

　A_－1＝｜1/2πi・∫_C－’g_T(z)e^zT(1＋z²/R²)／z dz｜

　A_－2＝｜1/2πi・∫_C－g(z)e^zT(1＋z²/R²)／z dz｜

とします。これから

　A≦A₊＋A_－≦A₊＋A_－1＋A_－2 → 2B/R（T→∞）→ 0 （R→∞）

を示します。

 

 

 

 

 

 

 

（3）A₊≦B/R、Re(z)＞0　を示します。

z＝Re^iθとおいて積分変数をzからθに変換すると、dz＝i Re^iθdθ

　　A₊≦1/2π｜∫_C＋｜g(z)－g_T(z)｜e^Re(z)T [1＋z²/R²]／z dz｜

非積分関数

[1＋z²/R²]／z＝[1＋R²e^2iθ/R²]/Re^iθ＝2[R(e^iθ＋e^－iθ)/2]/R²＝2Re(z) /R²

より

　　A₊≦1/2π∫_C＋｜g(z)－g_T(z)｜e^Re(z)T2Re(z) /R²｜dz｜

いま、｜f(t)｜≦B（有界）なので

｜g(z)－g_T(z)｜＝｜∫_[T，∞] f(t)exp[－zt] dt｜≦B｜∫_[T，∞] exp[－Re(z)t] dt｜

　　　　　　＝－B/ Re(z)[ exp[－Re(z)t]]_t＝T,∞＝B/ Re(z)・e^－Re(z)T

です。従って、

A₊≦1/2π∫_C＋B/ Re(z)・e^－Re(z)T・e^Re(z)T2Re(z) /R²｜dz｜＝(B/πR²) ∫_C＋｜dz｜

となります。∫_C＋｜dz｜＝πRより

　　A₊≦B/R

が得られます。

（4）A_－1＝｜1/2πi・∫_C－g_T(z)e^zT(1＋z²/R²)／z dz｜≦B/R　を示します。

Re(z)＜0より、C- ’の積分経路を用いる。｜Re(z)｜＝－Re(z)に注意して

　｜g_T(z)｜＝｜∫_[0，T] f(t)e^－zt dt｜≦B∫_[0，T] e^－Re(z)t dt＝B/(－Re(z))[e^－Re(z)t]t=0,T

　　　　　＝B/(－Re(z))[e^－Re(z)T－1]≦B/(－Re(z))e^－Re(z)T

　A_－1＝｜1/2πi・∫_C－’g_T(z)e^zT(1＋z²/R²)／z dz｜

　　　≦1/2π・∫_C－’｜g_T(z)｜e^Re(z)T｜(1＋z²/R²)／z｜｜dz｜

　　　≦1/2π・[B/(－Re(z))e^－Re(z)T] e^Re(z)T[2Re(z) /R²]・∫_C－’｜dz｜

　　　　＝1/2π・B/(－Re(z)) [2｜Re(z)｜/R²]・πR＝B/R

（5）A_－2＝｜1/2πi・∫_C－g(z)e^zT(1＋z²/R²)／z dz｜→ 0 as T→∞　を示す。

有界閉集合C－上のTを含まない複素関数の絶対値には最大値があり、

　｜g(z) (1＋z²/R²)/z｜≦M

なる正数Mが存在します。

　　A_－2≦M/2π・｜∫_C－e^zT dz｜≦M/2π・∫_C－e^Re(z)T｜dz｜

となる。C－上の積分路を弧AB上と直線BC上の2つに分けて、実行します。

1）弧AB上：z＝R e^iθ　(π/2≦θ≦λ)、cos(λ)＝－δ/R　｜dz｜＝Rdθ

2）直線BC上：z＝－δ＋it　(0≦t≦√(R²－δ²))　 ｜dz｜＝dt

実軸に対する対称性から、積分経路をIm(z)≧0に限定して、積分値を2倍します。

A_－2≦2・M/2π・[∫_AB e^Re(z)T｜dz｜＋∫_BC e^Re(z)T｜dz｜]

　　＝M/π・[∫_{[(π/2≦θ≦λ]} e^Rcos(θ)T Rdθ －∫_{[0≦t≦√(R2－δ2)]} e^－δT dt ]

t=cos(θ)とおくと、dt＝－sin(θ)dθ＝－√(1－t²) dθより、t：0→cos(λ)＝－δ/R

　＝M/π・[－∫_{[(0≦t≦－δ/R]} e^RTt R／√(1－t²) dt －√(R²－δ²)・e^－δT ]

　≦M/π・[－∫_{[(0≦t≦－δ/R]} e^RTt R／√(1－(δ/R)²) dt －√(R²－δ²)・e^－δT ]

　　＝M/π・[－R²／√(R²－δ²)・∫_{[(0≦t≦－δ/R]} e^RTt dt －√(R²－δ²)・e^－δT ]

ここで

　∫_{[(0≦t≦－δ/R]} e^RTt dt＝1/RT・[e^RTt]_{t＝0, －δ/R}＝1/RT・[e^－Tδ－1]

ですから、δ＞0より、

A_－2≦M/π・[R²／√(R²－δ²)・1/RT・[1－e^－Tδ]－√(R²－δ²)・e^－δT ] → 0 as T→∞

が得られます。

（3）～（5）より、

　　｜g(0)－g_T(0)｜＝A≦A₊＋A_－≦2B/R → 0  as  T→∞, R→∞

が成り立ちます。よって

　lim_[T→∞]g_T(0)＝g(0)

が存在することが証明されました。

 

＜コ－シ－の積分公式＞

領域Dで正則な複素関数f(z)のD内の閉曲線C上の積分に関して、Cで囲まれた領域の点z＝αにおいて

• f(α)＝1/2πi・∫_C f(z)／(z－α) dz

が成り立つ。Cの向きは反時計回りを正とする。

証明）z＝αの近傍で、正則関数f(z)を

• f(z)＝f(α＋z－α)＝f(α)＋f’(α) (z－α)＋1/2・f’’(α) (z－α)²＋・・・

と展開すると、正則関数1，z、z²、z³、・・は閉曲線C内に極をもたないので、コーシ－の積分定理よりC上の積分でゼロになります。

∫_C f(z)／(z－α) dz＝∫_C[f(α)＋f’(α) (z－α)＋1/2・f’’(α) (z－α)²＋・]／(z－α) dz

　＝f(α)・∫_C 1/(z－α) dz ＋f’(α)∫_C dz＋1/2・f’’(α) ∫_C (z－α) dz＋・・・

　＝f(α)・∫_C 1/(z－α) dz

となります。z＝α+e^iθとおくとdz＝ie^iθdθ、θ＝0～2πより

　∫_C 1/(z－α) dz＝∫_{[0≦θ≦2π]}i e^iθ/e^iθdθ＝2πi

従って

　∫_C f(z)／(z－α) dz＝2πi f(α)

となります。

 

＜モレラの定理＞～コ－シ－の積分定理の逆

閉曲線C上の連続関数f(z)の積分に関して、∫_C f(z)dz＝0　ならば、f(z)は閉曲線C内で正則である。

証明）z₀からzまでの積分経路をCとします。

　F(z)＝∫_C＝[z_0,z_] f(z)dz

zからz＋Δzまでの経路Lを、

• ξ(t)＝z＋Δz・t　(0≦t≦1)

で定義します。

• dz＝ξ’(t)dt＝Δzdt

が成り立ち、

　F(z＋Δz)＝∫_C+L f(z)dz

と書けます。以下にF(z)の導関数F’(z)が存在し、F’(z)＝f(z)となることを示します。

　　｜[F(z＋Δz)－F(z)]/ Δz－f(z)｜＝｜[∫_C+L f(z)dz－∫_C f(z)dz] /Δz－f(z)｜

　＝｜(1/Δz)∫_[z,z＋Δz] f(z)dz－f(z)｜＝｜(1/Δz)∫_[0,1] f(ξ(t)) Δzdt－f(z)｜

　＝｜∫_[0,1] f(ξ(t)) dt－f(z)｜

　≦∫_[0,1]｜f(ξ(t))－f(z)｜dt ≦∫_[0,1]εdt＝ε

ここでf(ξ)は連続なので、任意のε＞0に対して、｜f(ξ)－f(z)｜＜ε を満たす、｜ξ－z｜＜ΔzなるΔz＞0が存在します。ε→0とΔz→0は対応しています。

　Iim_[Δz→0]｜[F(z＋Δz)－F(z)]/ Δz－f(z)｜≦Iim_[Δz→0]ε(Δz)→0

よって、F(z)の導関数F’(z)が存在し、F’(z)＝f(z)となります。F(z)の導関数が存在するから、F(z)は正則です。グルサの定理より、F’(z)も正則になります。F’(z)＝f(z)なので、f(z)も正則になります。従って、閉曲線Cに対して、∫_C f(z)dz＝0　ならば、f(z)はC内で正則であることが示されました。

 

[Ⅶ] 素数定理　Lim _[x→∞] π(x) logx／x＝1　の証明

（1）Lim_[x→∞]π(x)log(x)/x≧1　を示します。

チェビシェフのシータ関数には

• θ(x)＝Σ_[p≦x] log(p)≦{Σ_[p≦x]1} log(x)＝π(x) logx

なる性質があります。x＞0について、[Ⅵ]より

• π(x) logx／x ≧ θ(x)／x　→1　as　x→∞

よって、Lim_[x→∞]π(x)log(x)/x≧1　となります。

（2）Lim_[x→∞] π(x) log(x)/x≦1　を示します。

任意のε＞0に対して、十分大きいxをとれば、ε・log(x)を大きくとることができるから、

　log(x)－ε・log(x)≦log(p)≦log(x)　→　0＜x^1－ε≦p≦x　

なる素数pが存在します。

θ(x)＝Σ_[p≦x] log(p) ≧ Σ[x^1－ε＜p≦x] log(p) ≧Σ[x^1－ε＜p≦x] log(x^1－ε)

　 ＝(1－ε)log(x)・Σ[x^1－ε＜p≦x]1＝(1－ε)log(x)・(π(x)－π(x^1－ε))

よって、

   θ(x) ≧(1－ε)log(x)・(π(x)－π(x^1－ε))

   θ(x)／x (1－ε) ≧π(x) log(x)/x－π(x^1－ε) log(x)/x

すなわち

  π(x) log(x)/x ≦ 1/(1－ε)・θ(x)/x＋π(x^1－ε) log(x)/x

                     ≦1/(1－ε)・θ(x)/x＋x^1－ε・log(x)/x

となる。ここで

    x^1－ε・log(x)/x＝log(x)/x^ε＝1/ε・log(x^ε)/x^ε

より、任意のε＞0に対して

  π(x) log(x)/x≦1/(1－ε)・θ(x)/x＋1/ε・log(x^ε)/x^ε　→　1/(1－ε)　as x→∞

が成り立つ。極限をとると

    Lim_[x→∞] π(x) log(x)/x≦1

となる。

（3）（1）と（2）から、素数定理

　　Lim_[x→∞] π(x) log(x)/x＝1

が証明されました。

 

[定理A]　Newmanの解析定理

t≧0で有界かつ可積分な関数f(t)に対して、

g(z)＝∫_[0，∞] f(t)exp[－zt] dt　Re(z)＞0

がRe(z)≧0で正則であれば、

　g(0)＝∫_[0，∞] f(t) dt

が存在する。つまり正則関数

　g_T(z)＝∫_[0，T] f(t)exp[－zt] dt

に対して、

lim_[T→∞]g_T(0)＝g(0)

が存在する。

[Ⅵ] θ(x)～x　の証明

　θ(x)～x の定義は、lim_[x→∞] θ(x)/x＝1　です。これは、任意のε＞0、∃x＞0に対して、

　　1－ε＜θ(x)/x＜1＋εと同値です。あるいは

• 任意のλ＞1に対してθ(x)＜λx　かつ
• 任意のλ＜1に対してλx＜θ(x)

と同値です。この命題を否定して、

• λ＞1に対してθ(x)≧λx　かつ
• λ＜1に対してλx≧θ(x)

なるλが存在するとして、矛盾を導きます。

（1）λ＞1に対してθ(x)≧λx　なるλが存在するとして、矛盾を導きます。

　λ＞1のとき、x≦t≦λxなるtに対して、θ(t)≧θ(x)であり

• θ(t)≧θ(x)≧λx　→　(θ(t)－t)／t²≧(λx－t)／t²

　であるから、

• ∫_[x,λx] [(θ(t)－t)／t²] dt ≧∫_[x,λx] [(λx－t)／t²] dt＝∫_[1,λ] [(λ－s)／s²] ds＝δ(λ)＞0

　が成り立ちます。ここでt=xsとおいて、積分変数をtからsに変換しました。

(Ⅴ)より積分

• F(x)＝∫_[1,x] [(θ(t)－t)／t²] dt　→　F（∞）as　x→∞

は収束するので、x→∞で

• 0＜δ(λ)≦∫_[x,λx] [(θ(t)－t)／t²] dt＝F(λx)－F(x)　→　0　as　x→∞

となり、矛盾することが示せました。

（2）λ＜1に対してλx≧θ(x)なるλが存在するとして、矛盾を導きます。

　λ＜1のとき、λx≦t≦xなるtに対して、θ(t)≦θ(x)であり、

• θ(t)≦θ(x)≦λx　→　(θ(t)－t)／t²≦(λx－t)／t²

　であるから、

• ∫_{[λx, x]} [(θ(t)－t)／t²] dt ≦∫_{[λx, x]} [(λx－t)／t²] dt＝∫_[λ,1] [(λ－s)／s²] ds＝δ(λ)＜0

　が成り立ちます。ここでt=xsとおいて、積分変数をtからsに変換しました。

　(Ⅴ)より積分

• F(x)＝∫_[1,x] [(θ(t)－t)／t²] dt　→　F（∞）as　x→∞

　は収束するので、x→∞で

• 0＞δ(λ)≧∫_{[λx, x]} [(θ(t)－t)／t²] dt＝F(x)－F(λx)　→　0　as　x→∞

　となり、矛盾します。よって背理法より、lim_[x→∞] θ(x)/x＝1　が示されました。

[Ⅴ]　∫_[1，∞] [θ(x)－x]／x² dxは収束する。

上記の積分の収束を命題[Ⅲ] 、[Ⅳ]、[定理A]を用いて5段階で証明します。

（1）　Φ(s)＝s∫_[1，∞] θ(x)／x^ｓ+1 dx、Re(s)＞1　が成り立つことを示します。

s∫_[1，∞] θ(x)／x^ｓ+1 dx＝s∫_[1，∞]Σ_[p≦x] log(p)／x^ｓ+1 dx

＝s∫_[1，2]0 dx＋s∫_[2，3] log2／x^ｓ+1dx＋s∫_[3，5](log2＋log3)／x^ｓ+1 dx＋・・・

＝－[log2／x^ｓ]_x=2,3－[(log2+log3)／x^ｓ]_x=3,5－[(log2+log3+log5)／x^ｓ]_x=5,7＋・・・

＝－(log2／3^s－log2／2^s)－[ (log2+log3)／5^s－(log2+log3)／3^s) ]

　－[ (log2+log3+log5)／7^s－(log2+log3+log5)／5^s) ]

　－[ (log2+log3+log5+log7)／11^s－(log2+log3+log5+log7)／7^s) ]－・・・

＝log2／2^s＋log3／3^s＋log5／5^s＋log7／7^s＋・・・

＝Σ_[p]logp／p^s ＝Φ(s)

（2）f(t)＝θ(e^t)e^－t－1　（t≧0）は有界かつ可積分である、ことを示します。

 (Ⅲ)でx＝e^tとして、あるＫ＞0が存在して、｜θ(e^t)｜≦Ｋe^t だから

   ｜f(t)｜＝｜θ(e^t)e^－t－1｜≦｜θ(e^t)｜e^－t＋1＝Ｋe^t e^－t＋1＝Ｋ＋1　

となり、f(t)は有界な関数である。

（3）g(z)＝Φ(z+1)／(z+1)－1/z　　Re(z)＞0　を示します。

x＝e^tとおいて置換積分を実施する。dx＝xdt、t：0→∞、x：1→∞、

e^－zt＝(e^t)^－z＝x^－zに注意すると、

　g(z)＝∫_[0，∞] (θ(e^t)e^－t－1)exp[－zt] dt

　　＝∫_[1，∞] (θ(x)x^－1) x^－z dx/x－[e^－zt／－z]_t=0,∞

　　＝∫_[1，∞] (θ(x)／x^z＋2)dx－1/z

　　＝Φ(z＋1)／(z＋1)－1/z

が示されました。

（4）g(z)はRe(z)≧0で正則である、ことを示します。

(Ⅲ)より、Φ(s)－1/(ｓ－1)はRe(s)≧1で正則なので、s＝z＋1として

　　Re(s)＝Re(z)＋1≧1　→　Re(z)≧0　

Φ(z＋1)－1/zはRe(z)≧0で正則なので、正則関数h(x)を用いて、

　　Φ(z＋1)－1/z＝h(x)　

と表せます。

　g(z)＝Φ(z＋1)／(z＋1)－1/z

　　　＝（h(x)＋1/z）／(z＋1)－1/z＝

　　　＝h(x)／(z＋1)＋1／z(z＋1)－1/z

　　　＝h(x)／(z＋1)＋[1－(z＋1)]／z(z＋1)

　　　＝[h(x)－1]／(z＋1)

　g(z)は、z=－1に極をもちますが、Re(z)≧0で正則であることが示されました。

（5）g(0)＝∫_[0，∞] f(t) dt＝∫_[1，∞] [θ(x)－x]／x² dx　が収束する、ことを示します。

　（2）より関数f(t)＝θ(e^t)e^－t－1はt≧0で有界かつ可積分であり、

　（4）よりg(z)＝∫_[0，∞] f(t)exp[－zt] dt がRe(z)≧0で正則である

従ってNewmanの解析定理により

　　g(0)＝∫_[0，∞] f(t) dt＝∫_[0，∞] (θ(e^t)e^－t－1) dt

が存在します。（3）と同様にx＝e^tとおいて置換積分を実施すると、

　　g(0)＝∫_[1，∞] (θ(x)x^－1－1) dx/x＝∫_[1，∞] [θ(x)－x]／x² dx

が収束することが示されました。

[Ⅳ] θ(x)＝Ｏ(x)　の証明

チェビシェフのシータ関数：θ(x)＝Σ_[p≦x] log(p) がオーダ－xであること、すなわち

・　∃ｋ＞0　｜θ(x)｜≦ｋx          

を3段階で証明します。

（1）2nlog2≧θ(2n)－θ(n)　の証明

2項定理より

2²ⁿ＝(1＋1)²ⁿ＝Σ_{[k＝1～2n] 2n}C_ｋ1^k1^2n-k≧_2nC_n＝2n・(2n－1)・(2n－2)・・(n+2)・(n+1)／n！

_2nC_nは自然数なので、分母のｎ！は約分されて1になります。しかしn+1＜p≦2nの素数pはn！の中には存在しないので、約分されずに分子に残ります。右辺はn+1＜p≦2nの素数pの積Π_{[n+1≦p≦2n]} pより大きくなるので、

・　2²ⁿ≧Π_{[n+1≦p≦2n]} p

が成り立ちます。一方

・　θ(2n)－θ(n)＝Σ_[p≦2n] log(p)－Σ_[p≦n] log(p)＝Σ_{[n+1≦p≦2n]} log(p)

なので、

・　exp[θ(2n)－θ(n)]＝exp[Σ_{[n+1≦p≦2n]} log(p)]＝Π_{[n+1≦p≦2n]} p

です。よって

・　2²ⁿ≧exp[θ(2n)－θ(n)]　→　2n・log2≧θ(2n)－θ(n)

が成り立ちます。

Eg.  ₁₆C₈=16・15・14・13・12・11・10・9／8・7・6・5・4・3・2・1

　　　　＝2・3・13・11 ＞11・13（8+1≦11,13≦16）

（2）2^ｍ+1・log2＞θ(2^m)　の証明

　上式にn＝2^k－1を代入すると、2^k・log2≧θ(2^k)－θ(2^k－1)が成り立つ。

k＝1：　2¹・log2≧θ(2¹)－θ(1)　

k＝2：　2²・log2≧θ(2²)－θ(2¹)

k＝3：　2³・log2≧θ(2³)－θ(2²)

・・・ 　　・・・・

k＝m－1：2^m－1・log2≧θ(2^m－1)－θ(2^m－2)

k＝m：　 2^m・log2≧θ(2^m)－θ(2^m－1)

をすべて加えると、θ(1)＝0より

　　log2・Σ_[k＝1～m]2^k ≧θ(2^m)

を得ます。ここで

　　Σ_[k＝1～m]2^k＝2^m+1－2＜2^m+1

だから、

　　2^m+1 log2＞θ(2^m)

が示されました。

(3) θ(x) ≦4log2・x

x≧1なる整数xに対して、∃m∊N、2^m≦x≦2^m+1

θ(x)は非減少関数なので、（2）より

　　0≦θ(x) ≦θ(2^m+1)＜2^m+2 log2≦4 log2・2^m≦4 log2・x

よって、K＝4 log2とおくと

　　θ(x) ≦Kx、　→　θ(x)＝O(x)

が示されました。

[Ⅲ] 　Φ(s)－1/(ｓ－1)はRe(s)≧1で正則である

という命題を5段階に分けて証明します。これは素数定理の証明で最も本質的な部分の証明です。

（1）ζ’(s)/ζ(s) ＋1/(s－1)　はRe(s)≧1で正則である、を示します。

　　ζ(s)‐1/(s－1)はRe(s)＞0で正則なので、係数a_nを用いて

・    ζ(s)＝1/(s－1)＋Σ_{[n＝0～∞]} a_n (s－1)ⁿ

と表示できます。項別微分ができるので、

・     ζ’(s)＝－1/(s－1)²＋Σ_{[n＝1～∞]} na_n (s－1)^n－1

となります。よって

　　　(s－1)ζ’(s)/ζ(s)

　　＝(s－1) [－1/(s－1)²＋Σ_{[n＝1～∞]} na_n (s－1)^n－1]／[1/(s－1)＋Σ_{[n＝0～∞]} a_n (s－1)ⁿ]

　　＝[－1＋Σ_{[n＝1～∞]} na_n (s－1)ⁿ⁺¹]／[1＋Σ_{[n＝0～∞]} a_n (s－1)ⁿ⁺¹]

　　→－1　as　s→1

つまり

• ζ’(s)/ζ(s) ＋1/(s－1)　はRe(s)≧1で正則である。

ことが示されました。

（2）Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)＋1/(s‐1)]－Σ[p] log(p)／p^s(p^s‐1) 　を示す。

ゼータ関数ζ(s)のオイラ－積表示

• ζ(s)＝Π[p] [1/(1‐1/p^s)]

の対数を取ると、

• log[ζ(s)]＝‐Σ[p] log(1‐1/p^s)

となります。これを微分した導関数は

• (1/p^s)′＝exp(‐slog(p))′＝‐log(p)／p^s

となります。よって

• ζ′(s)／ζ(s)＝‐Σ[p] (1‐1/p^s)′／(1‐1/p^s)＝‐Σ[p] log(p)/p^s／(1‐1/p^s)

より

• ζ′(s)／ζ(s)＝‐Σ[p] log(p)／(p^s‐1)

となります。ここでさらに

• 1/(p^s‐1)＝1/p^s＋1/ p^s(p^s‐1)

を用いると、

• ζ′(s)／ζ(s)＝‐Σ[p] log(p)／p^s－Σ[p] log(p)／p^s(p^s‐1)

つまり、ゼータ関数ζ(s)とファイ関数Φ(s)の関係式

• ζ′(s)／ζ(s)＝‐Φ(s)－Σ[p] log(p)／p^s(p^s‐1)　

が得られます。変形すると

• Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)＋1/(s‐1)]－Σ[p] log(p)／p^s(p^s‐1) 　

なる表式が得られました。

（3）右辺2項目Σ[p] log(p)／p^s(p^s‐1)はRe(s)＞1/2で正則である、を示します。

Re(s)＞1/2のとき

　｜p^s｜＞｜2^s｜＝2^Re(s) ＞√2

である。このとき

　　｜p^s｜＜(2＋√2)(｜p^s｜－1)　 →　1/(｜p^s｜－1)＜(2＋√2) /｜p^s｜

が成り立つ。理由は

　　　(2＋√2)＜ (1＋√2)｜p^s｜　→　√2＜｜p^s｜

　　　(2＋√2)/ (1＋√2)＝(2＋√2) (√2－1)＝2√2－2＋2－√2＝√2

従って

　　｜log(p)／p^s(p^s‐1)｜＜ log(p)／(｜p^s｜｜p^s‐1｜)＜ (2＋√2)・log(p)／p^2Re(s)

素数に関する和をとると
　　Σ[p]｜log(p)／p^s(p^s‐1)｜＜(2＋√2)・Σ[p] log(p)／p^2Re(s)＝(2＋√2)・Φ(2Re(s))

Φ(2Re(s))は2Re(s)＞1で収束するので、ワイヤストラスの収束判定定理よりRe(s)＞1/2の

領域で、Σ[p] log(p)／p^s(p^s‐1)は広義一様収束し、正則関数になることが示されました。

（4）Re(s)＝1でζ(s)＝0なる零点が存在しない、ことを示す。

複素共役変換：Conj(a+bi)＝a－bi、に関して

　　Conj[ζ(s)]＝ζ(Conj(s))

が成り立つ（鏡像原理）。なぜなら、

　　Conj[ζ(s)]＝Σ1/n^{Re(s)－Im(s)} ＝Σ1/n^Conj[s] ＝ζ(Conj(s))

だからです。実数a＞0に対して、

　　ζ(1＋ai)＝0　ならば　ζ(1－ai)＝0

　　ζ(1＋2ai)＝0　ならば　ζ(1－2ai)＝0

が成り立つ。

今、s＝1＋ai がζ(s)のu位の零点、s＝1＋2ai がζ(s)のv位の零点だとすると、

u≧0、v≧0なる整数を用いて

　ζ(s)＝b_u(s－1－ai)^u＋b_u+1(s－1－ai)^u+1＋b_u+2(s－1－ai)^u+2＋・・・

　ζ(s)＝C_v(s－1－2ai)^v＋C_v+1(s－1－2ai)^v+1＋C_v+2(s－1－2ai)^v+2＋・・・

と展開できます。鏡像原理から同様に、s＝1－ai がζ(s)のu位の零点、s＝1－2ai がζ(s)の

v位の零点となるので、

　ζ(s)＝b_u(s－1＋ai)^u＋b_u+1(s－1＋ai)^u+1＋b_u+2(s－1＋ai)^u+2＋・・・

　ζ(s)＝C_v(s－1＋2ai)^v＋C_v+1(s－1＋2ai)^v+1＋C_v+2(s－1＋2ai)^v+2＋・・・

と展開することもできます。各収束円内で項別微分して、

　ζ′(s)＝－1/(s－1)²＋a₁＋2a₂(s－1)＋3a₃(s－1)²＋・・・

　ζ’(s)＝ub_u(s－1∓ai)^u－1＋(u+1)b_u+1(s－1∓ai)^u＋(u+2)b_u+2(s－1∓ai)^u+1＋・・・

　ζ’(s)＝vC_v(s－1∓2ai)^v－1＋(v+1)C_v+1(s－1∓2ai)^v＋(v+2)C_v+2(s－1∓2ai)^v+1＋・・・

Φ関数に関して、

• 　Φ(s)＝－ζ′(s)／ζ(s)－Σ[p] log(p)／p^s(p^s‐1)　

が成り立っていました。このとき1）～3）の性質があります。

1) lim_[ε→0] εΦ(1+ε)＝1　e.　Φ(s)～1/(s－1)の項がある場合

　εΦ(1+ε)＝－εζ′(1+ε)／ζ(1+ε)－εΣ[p] log(p)／p^1+ε(p^1+ε‐1)　

　　＝－ε[－1/ε²＋a₁＋2a₂ε＋3a₃ε²＋・・・]/ [1/ε＋a₀＋a₁ε＋a₂ε²＋・・・]－O(ε)

　　＝[1－a₁ε²＋2a₂ε³＋3a₃ε⁴＋・・]/ [1＋a₀ε＋a₁ε²＋a₂ε²＋・・]－O(ε)

　　→1  as ε→0

2) lim_[ε→0] εΦ(1+ε±ai)＝－u　e.　Φ(s)～－u/(s－1∓ai)の項がある場合

　εΦ(1+ε±ai)＝－εζ′(1+ε±ai)／ζ(1+ε±ai)－εΣ[p] log(p)／p^1+ε±ai (p^1+ε±ai‐1)　

＝－ε[ub_uε^u－1＋(u+1)b_u+1ε^u＋(u+2)b_u+2ε^u+1＋・]/ [b_uε^u＋b_u+1ε^u+1＋b_u+2ε^u+2＋・] －O(ε)

＝－[ub_u＋(u+1)b_u+1ε＋(u+2)b_u+2ε²＋・・]/ [b_u＋b_u+1ε¹＋b_u+2ε²＋・・]－O(ε)

 →－u　as ε→0

3) lim_[ε→0] εΦ(1+ε±2ai)＝－v　e.　Φ(s)～－v/(s－1±2ai)の項がある場合

　εΦ(1+ε±2ai)＝－εζ′(1+ε±2ai)／ζ(1+ε±2ai)－εΣ[p] log(p)／p^1+ε±2ai (p^1+ε±2ai‐1)　

＝－ε[vC_vε^v－1＋(v+1)C_v+1ε^v＋(v+2)C_v+2ε^v+1＋・]/ [C_vε^v＋C_v+1ε^v+1＋C_v+2ε^v+2＋・]－O(ε)

＝－[vC_v＋(v+1)C_v+1ε＋(v+2)C_v+2ε²＋・・]/ [C_v＋C_v+1ε¹＋C_v+2ε²＋・・]－O(ε)

→－v　as ε→0

4）恒等式：

• [2Re(p^ia/2)]⁴＝p^2ia＋4p^ia＋6＋4p^－ia＋p^－2ia

が成り立つ。

[2Re(p^ia/2)]⁴＝[p^ia/2＋p^－ia/2]⁴＝[p^ia＋p^－ia＋2]²＝p^2ia＋p^－2ia＋4＋2 p^iap^－ia＋4 p^ia＋4 p^－ia

　               ＝p^2ia＋4p^ia＋6＋4p^－ia＋p^－2ia

5）εΣ_[p]log(p)/p^1+ε[2Re(p^ia/2)]⁴

　　＝εΦ(1＋ε－2ai)＋4εΦ(1＋ε－ai)＋6εΦ(1＋ε)＋4εΦ(1＋ε＋ai)＋εΦ(1＋ε＋2ai)

　　→　2(3－4u－v)　as ε→0

が成り立つ。

　　0＜εΣ_[p]log(p)/p^1+ε[2Re(p^ia/2)]⁴

　　　＝εΣ_[p]log(p)/p^1+ε[p^2ia＋4p^ia＋6＋4p^－ia＋p^－2ia]

　　　＝εΣ_[p]log(p)/p^1+ε－2ia＋4εΣ_[p]log(p)/p^1+ε+ia＋6εΣ_[p]log(p)/p^1+ε

　　　　　　　　　　　　　＋4εΣ_[p]log(p)/p^1+ε－ia＋εΣ_[p]log(p)/p^1+ε+2ia

　　　＝εΦ(1＋ε－2ai)＋4εΦ(1＋ε－ai)＋6εΦ(1＋ε)＋4εΦ(1＋ε＋ai)＋εΦ(1＋ε＋2ai)

　　　→　－v－4u＋6－4u－v ＝ 2(3－4u－v)＞0　as ε→0

6）ζ(s)はs＝1±aiに零点を持たない、を示す。

結局

• u≧0、v≧0、3－4u－v＞0　

より、u＝0　が結論される。任意の正数aに対して、ζ(s)はs＝1±aiに零点を持たない。

• ζ(s)＝b₀＋b₁(s－1±ai)＋b₂(s－1±ai)²＋・・・、b₀≠0

と展開できる。以上をまとめると

（1）ζ’(s)/ζ(s) ＋1/(s－1)　はRe(s)≧1で正則である。　

（2）Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)＋1/(s‐1)]－Σ[p] log(p)／p^s(p^s‐1)

（3）Σ[p] log(p)／p^s(p^s‐1)はRe(s)＞1/2で正則である。

（4）Re(s)＝1でζ(s)＝0なる零点が存在しない。

以上より、

• Φ(s)‐1/(s‐1)はRe(s)≧1で正則である。

と結論できます。

＜メモ＞

・Re(s)＞1で、オイラ－積　ζ(s)＝Π[p] [1/(1‐1/p^s)]が収束する

ことを示しておきましょう。

• 1/(1‐1/p^s)＝＝p^s/(p^s‐1)＝1＋1/(p^s‐1)

と書けます。今

｜p^s｜＝p^Re(s) ＞p≧2　より、　2｜p^s｜－｜p^s｜＞2　→　2(｜p^s｜－1)＞｜p^s｜＞0　

→　1/(｜p^s｜－1)＜2/｜p^s｜

が成り立ちます。

• ｜1/(p^s‐1)｜≦1/(｜p^s｜‐1)＜2/｜p^s｜＝2/p^Re(s)

が成り立ちます。素数pに対してn≦p＜n+1なる自然数nが存在します。

• f_n(s)＝δ_np/(p^s‐1)、M_n＝1/n^Re(s)

とすると、上の性質より

• ｜f_n(s)｜≦｜1/(p^s‐1)｜≦ 1/(｜p^s｜‐1)≦ 2/p^Re(s)≦ 2/n^Re(s)＝ M_n

であり、Re(s)＞1で

• Σ_{[n＝1～∞]} M_n＝ 2Σ_{[n＝1～∞]} 1/n^Re(s) ＝2ζ( Re(s))　が収束する。

従って、無限積の収束判定の定理より、オイラ－積

• Π_[n] [1＋f_n(s)]＝ Π_[n] [1＋δ_np/(p^s‐1)] ＝ Π_[p] [1＋1/(p^s‐1)]＝ Π_[p] [1/(1‐1/p^s)]

が収束します。

＜無限積の収束判定定理＞

関数列{f_n(s)}_{n＝1.2.3・・}に対して、正の数列{M_n} _{n＝1.2.3・・}が、任意のｓの領域において

1）｜f_n(s)｜≦M_n

2）Σ_{[n＝1～∞]} M_n＜∞

の2条件を満たすならば、無限積

• Π_{[n＝1～∞]} [1＋f_n(s)]

が収束する。

証明）　S_n＝Σ_[k=1～n] f_k(s)、P_n＝Π_[k＝1～n] [1＋f_k(s)]とする。

S_n＝Σ_[n=1～n] f_n(s)＜P_n＝Π_[k＝1～n] [1＋f_k(s)]＜Π_[k＝1～n]＝exp[Σ_[k＝1～n]f_k(s)]＝exp[S_n]

0＜｜S_n｜≦Σ_[n=1～n] M_n＜｜P_n｜＜exp[｜S_n｜] ≦exp[Σ_[n=1～n] M_n]

この関係は、n→∞では、

0＜｜S_∞｜≦Σ_[n=1～∞] M_n＜｜P_n＝∞｜＜exp[Σ_[n=1～∞] M_n]＜∞

となるので、Σ_[n=1～∞] M_nが収束するならば、｜P_n＝∞｜＝Π_{[n＝1～∞]} [1＋f_n(s)]が存在する。

注意：｜P_n＝∞｜が存在すれば、｜S_n＝∞｜も存在します。

リ－マンのゼータ関数ζ(s)は、

• ζ(s)＝Σ_{[n＝1～∞]} 1／n^s＝1＋1／2^s＋1／3^s＋・・・

Re(s)＞1で収束します。これをζ(s)のディリクレ級数表示ともいいます。

ｓ＞1ならば、2≦n≦Nに対して、n－1＜x＜nの時、

• 　1/n^s＜1/x^s＜1/(n－1)^s

が成り立つので、

• 1/n^s＜∫_[n－1,n]1/x^s dx ＜1/(n－1)^s
• Σ_[n=2～N] 1/n^s＜Σ_[n=2～N]∫_[n－1,n]1/x^s dx ＜Σ_[n=2～N] 1/(n－1)^s
• Σ_[n=2～N] 1/n^s＜∫_[1,N]1/x^s dx ＜Σ_[n=2～N] 1/(n－1)^s
• Σ_[n=1～N] 1/n^s－1＜∫_[1,N]1/x^s dx ＜Σ_{[n=1～N－1]} 1/n^s

ここで

• ∫_[1,N]1/x^s dx＝[x^1－S/(1－s)]x＝1,N　＝1/(s‐1)[1－N^1－s]＜1/(s‐1)

なので、

• Σ_[n=1～N] 1/n^s＜1＋1/(s‐1)　→　Σ_[n=1～∞] 1/n^sは収束する

従って

• 1/(s‐1) ≦ζ(s) ≦1＋1/(s‐1)　for s＞1

より、

• Lim_[s→+1] ζ(s)＝∞　かつ　Lim_[s→+1] (s‐1)ζ(s)＝1

が得られます。

 

s＝1のときは、ζ(s)は調和級数となり

• Σ_{[n＝1～∞]} 1／n＝1＋1／2＋1／3＋・・・＝log(∞)

対数発散をします。これは積分判定法から分かります。

積分判定法とは、正の単調減少関数f(x)によって、数列a_nを、a_n＝f(n)と定義すると、

• Σ_[n=1～∞] a_nが収束　⇔　∫_[1,∞] f(x) dxが収束

が成り立つというものです。よって

• ∫_[1,∞] 1/x dx＝log(∞)　→　Σ_{[n＝1～∞]} 1／n＝log(∞)

だと分かります。あるいは任意の正の整数ｋに対して

• Σ_[n=1～2k]1/n ＞ 1＋k/2　→　as k →∞

により示すことができます。

 

ゼータ関数ζ(s)のオイラ－積表示は

• ζ(s)＝Π_[p] [1/(1‐1/p^s)]

はディリクレ級数表示と一致するでしょうか。

s＞1のとき、有限積

• P_N(s)＝Π_[p≦N] [1/(1‐1/p^s)]

を考えます。

• 1/(1‐1/p^s)＝Σ_[k=0～∞] (p^－s)^k＝1＋1/p^s＋1/p^2s＋1/p^3s＋・・・

を代入して、P_N(s)を展開すると、素因数分解の一意性より

• Σ_[n＝1～N] 1/n^s ＜ P_N(s)＝Σ[nの各素因数≦N] 1/n^s ＜Σ_{[n＝1～∞]} 1/n^s＝ζ(s)

が成り立つので、

• Π_[p] [1/(1‐1/p^s)]＝Lim_[N→∞] P_N(s)＝ζ(s)

ゼータ関数ζ(s)はオイラ－積表示可能であることが示されました。

 

ゼータ関数ζ(s)は、s＞0（s≠1）に拡張することができます。

• ζ(s)＝L(s)／(1－2^1－s)　、L(s)＝Σ_{[n＝1～∞]}(－1)^(n－1)/n^s

右辺はs＞0（s≠1）で収束します。実際部分和L_N(s)＝Σ_[n＝1～N](－1)^(n－1)/n^sを考えると、

• 0＜1－1/2^s＝L₂＜L₄＜・・・＜L_2N＜L_2N+2＜L_2N+1＜L_2N－1＜・・・＜L₃＜L₁＝1

偶数番目の部分和L_2nは上に有界で単調増加、奇数番目の部分和L_2n-1は下に有界で単調減少なので、それぞれ収束し、s＞0のとき

• L_2N－L_2N-1＝－1/(2N)^s　→ 0 　as 　N →∞

だから、

• Lim_[N→∞] L_2N＝Lim_[N→∞]L_2N-1＝L(s)

となります。

• ζ(s)‐L(s)＝2Σ_{[n＝1～∞]}1/(2n)^s＝2^(1－s)・Σ_{[n＝1～∞]}1/n^s＝2^(1－s) ζ(s)

よって、

• ζ(s)＝L(s)／(1－2^1－s)　for　s＞0（s≠1）

が示されました。s＞0のときは、ζ(s)はL(s)/(1－2^1－s)だと再定義します。

0＜s＜1のとき、L(s)＞0で(1－2^1－s)＜0なので、ζ(s)＜0であり、

• Lim_[s→1-δ] ζ(s)＝－∞

となります。正の関数を解析接続すると負の関数になるのは驚きです。

実はガンマ関数を用いると、s＜0の領域にもζ(s)を拡張することができます。

結果だけ書くと、

• ζ(s)＝2^sπ^s‐1・sin(πs/2)・Γ(1－s)・ζ(1－s)　 s＜0（s≠1）

右辺は1－s＞1で定義されるので、左辺はｓ＜0で定義できます。

• sin(πs/2)＝0　for　s＝－2、－4、－6、・・・

なので、

• ζ(－2k)＝0　（kは正の自然数）

となります。これらの負の零点をゼータ関数の自明な零点といいます。

下図にゼータ関数の外形を示します。N＝10000までの和で計算表示しました。本来、赤線と青線はｓ＝0でｙ＝－1/2で接続します。ｓ＜0の部分は、振動しており、負の偶数は零点になっています。

 

実数x以下の素数の個数π(x)は

• π(x)＝Σ_[p≦x] 1

と表せます。π(x)は「素数ｐ（＝2、3，・・・Ｐ≦x）がx以下の最大の素数Pになるまで1を加え続ければ得られます。π(x)は素数を段差とする階段関数になっています。素数定理は

• π(x)～x／logx

すなわち

• Lim _[x→∞] π(x) logx／x＝1

が成り立つというものです。

まずチェビシェフのシータ関数

• θ(x)＝Σ_[p≦x] log(p)

を考えます。この関数には

• θ(x)≦π(x) logx

なる性質があります。実際

• θ(x)＝Σ_[p≦x] log(p)≦{Σ_[p≦x]1} log(x)＝π(x) logx

によって確かめられます。

• π(x) logx／x ≧ θ(x)／x　→1　as　x→∞

ですから、素数定理を示すのに、

• Lim _[x→∞] θ(x)／x＝1

すなわち

• θ(x)～x

が成り立つことを示す必要があります。これは任意のλに対して

• ∀ λ＞1 θ(x)≦λx　かつ　∀ λ＜1　θ(x)≦λx

が成り立つことと同値です。この命題を否定して、

• θ(x)≧λx　for　λ＞1　あるいは　θ(x)≦λx　for　λ＜1

なるλが存在するとして、矛盾を導きます。　x≦t≦λxなるtに対して

• θ(t)≧θ(x)≧λx　→　(θ(t)－t)／t²≧(λx－t)／t²

であるから、

• ∫_[x,λx] [(θ(t)－t)／t²] dt ≧∫_[x,λx] [(λx－t)／t²] dt＝∫_[1,λ] [(λ－s)／s²] ds＝δ(λ)＞0

が成り立ちます。ここでt=sxとおいて、積分変数をtからsに変換しました。積分

• F(x)＝∫_[1,x] [(θ(t)－t)／t²] dt　→　F（∞）as　x→∞

が収束すれば、左辺の極限値がゼロ

• 左辺＝F(λx)－F(x)　→　0　as　x→∞

になり、左辺≧δ(λ)＞0に矛盾することが示せます。

先ほどの積分は、x＝exp(t) と置いて、xからtに変数変換すると、dx＝xdt

• F(∞)＝∫_[1,∞] [(θ(x)－x)／x²] dx＝∫_[0,∞] (θ(e^t) e‐^t－1) dt＝∫_[0,∞] f(t) dt
• f(t)＝θ(e^t) e‐^t－1

と書けます。ここで、f(t)のラプラス変換

• g(z)＝∫_[0,∞] f(t) e^－zt dt

を考えます。Newman教授は、f(t)が有界で、複素関数g(z)がRe(z)≧0で正則ならば、

• g(0)＝∫_[0,∞] f(t) dt

が存在するという解析定理を発見しました。

注意すべきことは、一般に

• Lim_[z→0] ∫_[0,∞] f(t) e^－zt dt = ∫_[0,∞] f(t) dt

が成立しないことです。例えばf(t)＝sin(t)のとき

• g(z)＝∫_[0,∞] sin(t) e^－zt dt＝1/(z²＋1) → 1　as　z→0

となります。しかしg(0)＝∫_[0,∞] sin(t) dtは存在しません。計算を示します。

• g(z)＝∫_[0,∞] 1/2i・(e^it‐e^－it) e^－zt dt=1/2i・[e^it－zt/(i－z)+e^－it－zt/(i＋z)]t=0,∞

＝－1/2i・[1/(i－z)＋1/(i＋z)]＝1/(z²＋1)

実際シ－タ関数は、ある正数Kに対して

• θ(x)≦Kx　e.　 θ(x)＝O(x)：オーダ－ｘ

なる性質があるので、

• ｜f(t)｜＝｜θ(e^t) e‐^t－1｜≦θ(e^t)／e^t＋1≦K＋1

となり、f(t)が有界になります。

複素関数g(z)は、x=exp(t)と変数変換すると、dx=xdt、e^－zt＝1/x^z

• g(z)＝∫_[0,∞] (θ(e^t) e‐^t－1) e^－zt dt＝∫_[1,∞] (θ(x)／x^z+2) dx‐1/z

となります。θ(x)を代入して計算すると

• g(z－1)＝∫_[1,∞] (Σ[p≦x] log(p)／x^z+1) dx‐1/z＝Φ(z)/z‐1/z

なる関係が得られます。

• z∫_[1,∞] (θ(x)／x^z+1) dx＝z∫_[2,3] log2／x^z+1 dx＋z∫_[3,5] (log2+ log3)／x^z+1 dx＋・・・

＝－[log2/x^z]x=2,3－[(log2+log3)/x^z]x=3,5－[(log2+log3+log5)/x^z]x=5,7＋・・・

＝(－log2/3^z+ log2/2^z)－[－(log2+log3)/5^z－(log2+log3)/3^z)]

－[－(log2+log3+ log5)/7^z－(log2+log3+ log5)/5^z)]＋・・・

　　＝log2/2^z＋log3/3^z)＋log5/5^z＋log7/7^z＋・・・

＝Σ_[p] log(p)／p^z＝Φ(z)

関数Φ(s)は

• Φ(s)＝Σ_[p] log(p)／p^s

ここでΣ_[p]は全ての素数の和を取ります。結局

• g(z)＝Φ(z+1)／(z+1)－1/z＝[{Φ(z+1)－1/z}－1]／(z+1)

Newmanの解析定理を適用するには、g(z)がRe(z)≧0で正則でなければなりません。

よって

• Φ(s)－1/(s‐1)がRe(s)≧1で正則である

ことが言えれば良いことが分かります。

ここでリ－マンのゼータ関数ζ(s)

• ζ(s)＝Σ_{[n＝1～∞]} 1／n^s＝1＋1／2^s＋1／3^s＋・・・

を考えます。この関数はRe(s)＞1で収束します。s＝1のときは、ζ(s)は調和級数となり

• Σ_{[n＝1～∞]} 1／n＝1＋1／2＋1／3＋・・・＝log(∞)

対数発散をします。自然数の素因数分解の一意性によって、ゼータ関数ζ(s)は

• ζ(s)＝Π_[p] [1/(1‐1/p^s)]

とも書けます。これをオイラ－積表示といいます。実際

• ζ(s)＝ [1/(1‐1/2^s)]・[1/(1‐1/3^s)]・[1/(1‐1/5^s)]・[1/(1‐1/7^s)]・[1/(1‐1/11^s)]・・・

　　　 ＝[1＋1/2^s＋1/2^2s＋1/2^3s＋1/2^4s＋1/2^5s＋・・・]

・[1＋1/3^s＋1/3^2s＋1/3^3s＋1/3^4s＋1/3^5s＋・・・]

・[1＋1/5^s＋1/5^2s＋1/5^3s＋1/5^4s＋1/5^5s＋・・・]

・[1＋1/7^s＋1/7^2s＋1/7^3s＋175^4s＋1/7^5s＋・・・]・・・

      　＝1＋1／2^s＋1／3^s＋1／2^2s＋1／5^s＋1／2^s3^s＋1／7^s＋1／2^3s＋1／3^2s＋1／2^s 5^s

＋1／11^s＋1／2^2s3^s＋1／13^s＋1／2^s7^s＋1／3^s 5^s＋1／2^4s＋・・・

　　　　＝1＋1／2^s＋1／3^s＋1／4^s＋1／5^s＋1／6^s＋1／7^s＋1／8^s＋1／9^s＋1／10^s

＋1／11^s＋1／12^s＋1／13^s＋1／14^s＋1／15^s＋1／16^s＋・・・

となり、成立しています。ζ(s)のオイラ－積表示の対数を取ると、

• log[ζ(s)]＝‐Σ_[p] log(1‐1/p^s)

となります。これを微分した導関数は

• (1/p^s)′＝exp(‐slog(p))′＝‐log(p)／p^s

となります。よって

• ζ′(s)／ζ(s)＝‐Σ_[p] (1‐1/p^s)′／(1‐1/p^s)＝‐Σ_[p] log(p)/p^s／(1‐1/p^s)

より

• ζ′(s)／ζ(s)＝‐Σ_[p] log(p)／(p^s‐1)

となります。ここで

• 1/(p^s‐1)＝1/p^s＋1/ p^s(p^s‐1)

を用いると、

• ζ′(s)／ζ(s)＝‐Σ_[p] log(p)／p^s－Σ_[p] log(p)／p^s(p^s‐1)

つまり、ゼータ関数ζ(s)とファイ関数Φ(s)の関係式

• ζ′(s)／ζ(s)＝‐Φ(s)－Σ_[p] log(p)／p^s(p^s‐1)　

が得られます。変形すると

• Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)‐1/(1－s)]－Σ_[p] log(p)／p^s(p^s‐1) 　　・・・（＃）

なる表式が得られます。実は右辺2項目はRe(s)＞1/2で正則です。

Φ(s)－1/(s‐1)がRe(s)≧1で正則であることを示すためには、

• ζ′(s)／ζ(s)‐1/(1－s)がRe(s)≧1で正則である

ことを示す必要があります。そのためには

• ζ(s)がRe(s)＝1で零点を持たない。
• ζ(s)‐1/(s‐1)はRe(s)＞0で正則である。

ことを示す必要があります。なぜならそれが成り立てば、ζ(s)はRe(s)＞0でs＝1に極を持つ有理型関数なので、

• Lim_[s→1] (1－s) ζ′(s)／ζ(s)＝1　 for　Re(s)＞1

となるからです。いま

• 1/(s‐1)＝Σ_[n=1～∞] ∫_[n,n+1]1/x^sdx

と書けるので

• ζ(s)‐1/(s‐1)＝Σ_[n=1～∞][1/n^s‐∫_[n,n+1]1/x^sdx]＝Σ_[n=1～∞]∫_[n,n+1][1/n^s‐1/x^s]dx
• ｜∫_[n,n+1][1/n^s‐1/x^s]dx｜≦｜s｜/n^Re(s)+1
• ｜ζ(s)‐1/(s‐1)｜≦Σ_[n=1～∞]｜s｜/n^Re(s)+1＝｜s｜ζ(Re(s)+1)

となります。ζ(Re(s)+1)はRe(s)+1＞1で正則なので、ζ(s)‐1/(s‐1)はRe(s)＞0で正則関数に拡張できます。つまり素数定理の核心はζ(s)がRe(s)＝1で零点を持たないことの証明になります。

 

ゼータ関数ζ(s)のオイラ－積表示

• ζ(s)＝Π_[p] [1/(1‐1/p^s)]

は興味深い関係式です。もしゼータ関数の零点ρが分かれば、

• ζ(s)＝f(s)・Π_[ρ] [s－ρ]

と因数分解できることになります。対数表示をとると

log f(s)＋Σ_[ρ]log (s‐ρ)＝－Σ_[p] log (1‐1/p^s)

が得られます。これはゼータ関数の零点ρに関する和が、全ての素数pに関する和と関係があることを示唆しています。ゼータ関数の零点には、素数の情報が含まれていると考えられます。ゼータ関数はs=－2k＝－2、－4、－6、・・・に自明な零点を持つことが知られています。ζ(0)＝－1/2で、s=0は零点ではありません。

• ゼータ関数の非自明な零点は、Re(1/2)上に存在している

というのが、有名なリーマン予想です。10兆個の零点を調べたところ、全てRe(1/2)上に存在しているようです。しかしその事実を持って、リーマン予想が正しいと結論することはできません。フラクタル曲線で有名なコッホは1901年に、リーマン予想が正しければ、素数の計数関数は

• π(x)～Li(x)＋O(√ｘ・log(x))

と書けると主張しています。リーマン予想は素数分布の予測の精緻化にも役立ちます。

リーマン予想は数論の様々な問題と関連しており、今でも高い関心が注がれています。

＜素数定理＞

自然数x以下の素数の個数をπ(x)とすると、π(x)～x／logxと表される。すなわち

• Lim _[x→∞] π(x) logx／x＝1

が成り立つ（1896年）。

素数定理は1896年にジャック・アダマ－ルとバレ・プ－サンによって独立に証明されました。素数定理は簡潔で分かりやすい定理ですが、証明は難解です。1949年にアトル・セルバ－グやポール・エルディッシュが初等的手法で証明しました。初等的といっても、証明法は技巧的で難いものです。

1980年にドナルド・ニュ－マンが複素関数論を用いて簡潔な素数定理の証明方法を見つけました。1997年に素数定理100周年記念として、ドン・ザギエが5つのステップと解析的定理を用いるニュ－マンの証明法を紹介しました。ここではニュ－マンとザギエによる素数定理の証明を紹介します。複素関数論の威力が良く分かります。

ザギエ教授の経歴

ザギエは西ドイツのハイデルベルクに生まれた。母親は精神科医で、父親はスイスのアメリカン・カリッジの教頭だった。父親が5つの異なる市民権を有していたため、ザギエは若いころ多くの国々で過ごしていた。13歳の時に高校を卒業し、1年間ウィンチェスター・カレッジにて学んだ後、ザギエはMITで3年間学び、学士号と修士号を得、1967年16歳の時プットナム・フェローに指名された。ザギエはボン大学でフリードリッヒ・ヒルツェブルフの下で特性類に関する博士論文を書き、20歳の時に博士号を受けた。23歳の時に教授資格を受け、24歳の時に教授に指名された。

[1] Donald J. Newman, (1980). “Simple analytic proof of the prime number theorem”. American Mathematical Monthly. 87 (9): 693–696.

[2] Don Zagier, (1997). “Newman’s Short Proof of the Prime Number Theorem”. Amer. Math. Monthly 104 (8): 705–708. ショーヴネ賞 (2000)

 

現代情報社会に欠かせなくなった暗号には素数の性質が使われています。素数は1と自分自身以外で割り切れない数のことです。具体的には

• 素数＝{2，3、5、7、11，13，17、19、23、・・・}

なる自然数です。素数には1を含めません。そうすると全ての数は素数の積として一意に表すことができます。いわば素数は自然界の原子のような存在です。しかし素数は無限にあります。

自然数n以下の素数の個数をπ(n)と表します。図1にｙ＝π(x)のグラフを示します。例えば50番目の素数229と95番目の素数499はそれぞれ（229，50）と（499，95）にプロットされています。500以下には95個の素数があるので、π(500)＝95です。

驚くべきことに、素数の出現の仕方には規則性がないのに、素数はほぼ一つの曲線の近傍に分布しているように見えますが、その理由は今でも良く分かっていません。お子さんに素数の分布曲線を見せることで、未知の法則に対する興味関心を引き出すことができるでしょう。

素数を見出す確率はどのくらいでしょうか。1792年にドイツの数学者ガウス（当時15歳）は、数ｎの近傍で素数を見出す確率は1／log(n)と予想しました。その場合に自然数n以下の素数の個数は

• Li(n)＝∫_[2→n] 1/log(t) dt

と表せます。ここでlogは自然対数です。展開近似すると

• Li(n)≒n/log(n)+n／(log(n))＾2　→　n/log(n)　as ｎ→∞

となります。ｎ→∞の極限で両者が一致するという意味で

• Li(n)～n/log(n)

と書き表します。実際に

• π(n)～Li(n)

となっています。ｘが大きい数のとき、ｘまでの数の中に素数を見出す確率π(x)／xは、1／log(x)、すなわち

• π(x)～f(x)＝x／log(x)

と考えられます。図2に10万までの素数の分布曲線を示します。10万程度ではx/log(x)の近似は誤差が大きいことが分かります。

この定理を使うと、例えば100億までに約4.5億個の素数があることがすぐに計算できます。

x＝10ⁿのとき、

• f(10ⁿ)＝10ⁿ／log(10ⁿ)＝log(e)／n・ 10ⁿ≒log（27/10）／n・ 10ⁿ

　　　　＝(3log3－1) ／n・ 10ⁿ≒(0.434／n)×10ⁿ

x＝100億=10¹⁰の時、素数の数は

• f(10¹⁰)≒434／10・ 10¹⁰＝4.34億個

と予想されます。実際、100億より小さい素数の数は

• π(10¹⁰ )­＝455,052,511＝4.55億個

なので、4.6％の誤差で当たっています。Li(x)の場合、

• Li(10¹⁰) ≒ 455,055,615

なので、0.0007%の誤差しかありません。