＜素数定理＞

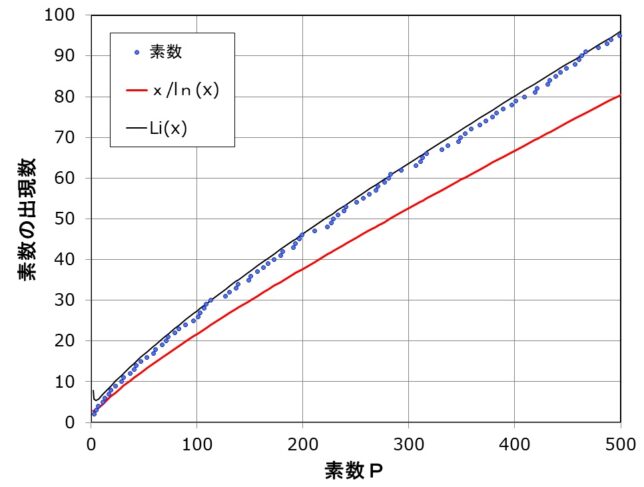
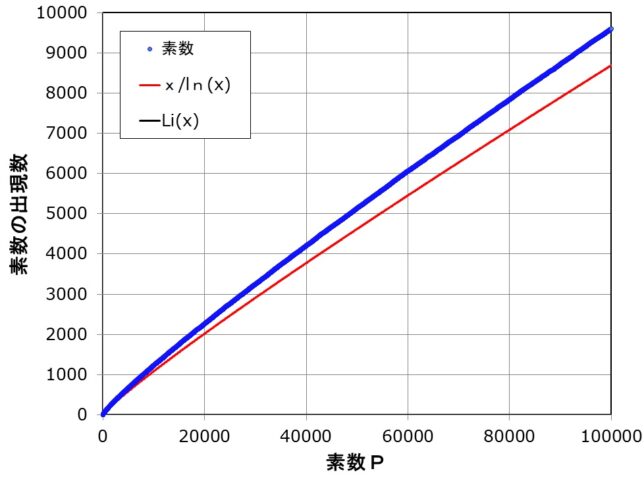
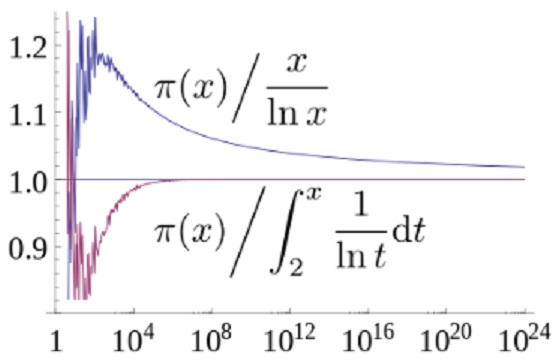
自然数x以下の素数の個数をπ(x)とすると、π(x)～x／logxと表される。すなわち

• Lim _[x→∞] π(x) logx／x＝1

が成り立つ（1896年）。

素数定理は1896年にジャック・アダマ－ルとバレ・プ－サンによって独立に証明されました。素数定理は簡潔で分かりやすい定理ですが、証明は難解です。1949年にアトル・セルバ－グやポール・エルディッシュが初等的手法で証明しました。初等的といっても、証明法は技巧的で難いものです。

1980年にドナルド・ニュ－マンが複素関数論を用いて簡潔な素数定理の証明方法を見つけました。1997年に素数定理100周年記念として、ドン・ザギエが5つのステップと解析的定理を用いるニュ－マンの証明法を紹介しました。ここではニュ－マンとザギエによる素数定理の証明を紹介します。複素関数論の威力が良く分かります。

ザギエ教授の経歴

ザギエは西ドイツのハイデルベルクに生まれた。母親は精神科医で、父親はスイスのアメリカン・カリッジの教頭だった。父親が5つの異なる市民権を有していたため、ザギエは若いころ多くの国々で過ごしていた。13歳の時に高校を卒業し、1年間ウィンチェスター・カレッジにて学んだ後、ザギエはMITで3年間学び、学士号と修士号を得、1967年16歳の時プットナム・フェローに指名された。ザギエはボン大学でフリードリッヒ・ヒルツェブルフの下で特性類に関する博士論文を書き、20歳の時に博士号を受けた。23歳の時に教授資格を受け、24歳の時に教授に指名された。

[1] Donald J. Newman, (1980). “Simple analytic proof of the prime number theorem”. American Mathematical Monthly. 87 (9): 693–696.

[2] Don Zagier, (1997). “Newman’s Short Proof of the Prime Number Theorem”. Amer. Math. Monthly 104 (8): 705–708. ショーヴネ賞 (2000)

 

現代情報社会に欠かせなくなった暗号には素数の性質が使われています。素数は1と自分自身以外で割り切れない数のことです。具体的には

• 素数＝{2，3、5、7、11，13，17、19、23、・・・}

なる自然数です。素数には1を含めません。そうすると全ての数は素数の積として一意に表すことができます。いわば素数は自然界の原子のような存在です。しかし素数は無限にあります。

自然数n以下の素数の個数をπ(n)と表します。図1にｙ＝π(x)のグラフを示します。例えば50番目の素数229と95番目の素数499はそれぞれ（229，50）と（499，95）にプロットされています。500以下には95個の素数があるので、π(500)＝95です。

驚くべきことに、素数の出現の仕方には規則性がないのに、素数はほぼ一つの曲線の近傍に分布しているように見えますが、その理由は今でも良く分かっていません。お子さんに素数の分布曲線を見せることで、未知の法則に対する興味関心を引き出すことができるでしょう。

素数を見出す確率はどのくらいでしょうか。1792年にドイツの数学者ガウス（当時15歳）は、数ｎの近傍で素数を見出す確率は1／log(n)と予想しました。その場合に自然数n以下の素数の個数は

• Li(n)＝∫_[2→n] 1/log(t) dt

と表せます。ここでlogは自然対数です。展開近似すると

• Li(n)≒n/log(n)+n／(log(n))＾2　→　n/log(n)　as ｎ→∞

となります。ｎ→∞の極限で両者が一致するという意味で

• Li(n)～n/log(n)

と書き表します。実際に

• π(n)～Li(n)

となっています。ｘが大きい数のとき、ｘまでの数の中に素数を見出す確率π(x)／xは、1／log(x)、すなわち

• π(x)～f(x)＝x／log(x)

と考えられます。図2に10万までの素数の分布曲線を示します。10万程度ではx/log(x)の近似は誤差が大きいことが分かります。

この定理を使うと、例えば100億までに約4.5億個の素数があることがすぐに計算できます。

x＝10ⁿのとき、

• f(10ⁿ)＝10ⁿ／log(10ⁿ)＝log(e)／n・ 10ⁿ≒log（27/10）／n・ 10ⁿ

　　　　＝(3log3－1) ／n・ 10ⁿ≒(0.434／n)×10ⁿ

x＝100億=10¹⁰の時、素数の数は

• f(10¹⁰)≒434／10・ 10¹⁰＝4.34億個

と予想されます。実際、100億より小さい素数の数は

• π(10¹⁰ )­＝455,052,511＝4.55億個

なので、4.6％の誤差で当たっています。Li(x)の場合、

• Li(10¹⁰) ≒ 455,055,615

なので、0.0007%の誤差しかありません。