＜マンゴルトの明示公式＞

前回チェビシェブ関数の積分表示

   Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} ζ'(s)/ζ(s)・x^s/s ds

を求めました。今回は積分を実行し、マンゴルトの明示公式を導出します。

　f_x(s)＝ζ'(s)/ζ(s)・x^s/s

とおくと

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds＝－1/2πi・∫_C1 f_x(s)ds

となります。この複素積分を閉曲線C(c,T,R）

　C(c,T,R)＝C_{1[c－Ti、c＋Ti]}＋C_{2[c+Ti、－R＋Ti]}＋C_{3[－R＋Ti、－R －Ti]}＋C_{4[－R－Ti、c－Ti]}

に拡張すると、

　lim_[R,T→∞]∫_C2 f_x(s)ds＝lim_[R,T→∞]∫_C3 f_x(s)ds＝lim_[R,T→∞]∫_C4 f_x(s)ds＝0

となるので、

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds

　　　　＝－1/2πi・lim_[R,T→∞]∫_C(c,T,R）f_x(s)ds

となります。閉曲線内に含まれるf_x(s)の極の留数を計算すれば、Ψ^*(x)を求めることができます。

＜マンゴルトの明示公式＞

チェビシェフの素数pの階段関数

　Ψ^*(x)＝Σ[n≦x]Λ(n)＝Σ[p^m≦x] log(p)

に関して

　Ψ^*(x)＝x－1/2・log(1－x^－2)－log 2π－Σ’_ρ∊Z0x^ρ/ρ

がなりたつ。ここでZ₀＝｛ｓ｜ζ(s)＝0なる非自明な零点｝である。マンゴルトの明示公式は、素数の分布を表す階段関数Ψ^*(x)がゼ－タ関数の非自明な零点の和を含むｘの解析関数によって書かれているという不思議な公式です。

閉曲線内の

　f_x(s)＝ζ'(s)/ζ(s)・x^s/s

の零点は、ρ＝1、－2n、0、ρ_iの4種類あります。

まずζ'(s)/ζ(s)の留数を考えます。

　ζ(s)～1/(s－1)+・・

　ζ'(s)～－1/(s－1)²+・・

　ζ'(s)/ζ(s)～－1/(s－1)+・・

なので、極をρとすると、位数Ord(ζ,ρ)について

　Res(ζ’/ζ,ρ)＝Ord(ζ,ρ)

が成り立ちます。偏角の原理より、留数は

　Res(ζ'(s)/ζ(s)・x^s/s,ρ)＝Ord(ζ,ρ) x^ρ/ρ

となります。

1）s＝1の留数

　Ord(ζ,1)＝－1となります。

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝1)＝Ord(ζ,1) x¹/1＝－x

2）s＝－2nの留数

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝－2n)＝Ord(ζ,1) x^－2n/(－2n)

R→∞でN→∞となるので

　－lim_[N→∞]Σ_n＝1～N x^－2n/(－2n)＝1/2・log(1－x^－2)

3）s＝0の留数

　　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝0)＝ζ'(0)/ζ(0)＝log(2π)

　　ζ(0)＝－1/2、ζ’(0)＝－1/2・log(2π)

4）ｓの非自明な零点ρ_iの留数

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝ρ_i)＝Ord(ζ,ρ_i) x^ρi /ρ_i

T→∞でN→∞となるので

　lim_[N→∞]Σ_i＝1～N Ord(ζ,ρ_i) x^ρi /ρ_i＝Σ’_ρ∊Z0 x^ρ /ρ

Σ’_ρ∊Z0は非自明な零点ρでの位数がｍの場合ｍ回和をとると言う意味です。

以上から、マンゴルトの明示公式

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds

　　　　＝－1/2πi・lim_[R,T→∞]∫_C(c,T,R）f_x(s)ds

　　　　＝－1/2πi・2πi・（－x＋1/2・log(1－x^－2)＋log 2π＋Σ’_ρ∊Z0 x^ρ /ρ）

　　　＝x－1/2・log(1－x^－2)－log 2π－Σ’_ρ∊Z0 x^ρ /ρ

が成り立ちます。

偏角原理とは、z=z₀でm位の特異点をもちそれ以外で正則な関数f(z)に関して

　Res(f’/f,z₀)＝Ord(f,z₀)＝m

が成り立つ定理です。f(z)は、z=z₀で特異点をもたない正則関数g(z)を用いて

　f(z)＝(z－z₀)^m・g(z)

と書けます。このとき、

　f'(z) /f(z)＝[m(z－z₀)^m－1・g(z)＋(z－z₀)^m・g'(z)]/ (z－z₀)^m・g(z)

　　　　　＝m/(z－z₀)＋g'(z)/ g(z)

なので、f'(z) /f(z)はz＝z₀で1位の極を持つことがわかり

　Res(f’/f,z₀) ＝m＝Ord(f,z₀)

が成り立ちます。

＜マンゴルト関数Λ(n)とチェビシェフ関数Ψ(x)＞

自然数nに対して、マンゴルト関数Λ(n)を

　　Λ(n)＝log(p)　if　n＝p^m, 　otherwise 0

と定義します。ここでpは素数です。具体的には

　Λ(1)＝0、Λ(2)＝log2、Λ(3)＝log3、Λ(4)＝Λ(2²)＝log2、Λ(5)＝log5、

　Λ(6)＝Λ(2・3)＝0、Λ(7)＝log7、Λ(8)＝Λ(2³)＝log2、Λ(9)＝Λ(3²)＝log3、

　Λ(10)＝Λ(2・5)＝0、Λ(11)＝log11、Λ(12)＝Λ(2・2・3)＝0、・・・

です。単一の素数のべき乗でのみΛ値がゼロではありません。

実数xに対して、チェビシェフ関数Ψ(x)を

　　Ψ(x)＝Σ_[n≦x]Λ(n)＝Σ_[p^m_≦x] log(p)

と定義します。ここでpは素数です。Σ_[p^m≦x]は、x以下の素数pの冪乗となっている素数pで和をとることを意味します。Ψ(x)は階段関数です。

ｘ＝5とすると

　　Ψ(5)＝Λ(1)＋Λ(2)＋Λ(3)＋Λ(4)＋Λ(5)＝0＋log2＋log3＋log2＋log5

となります。Ψ(x)のステップアップする点で、ステップアップ部分の中点をとる関数をΨ^*(x)と書きます。

　　Ψ^*(5)＝log2＋log3＋log2＋1/2・log5

となります。Ψ^*(x)では最後の項が1/2倍になります。ｘ＝9の場合は

　　Ψ(9)＝Λ(1)＋Λ(2)＋Λ(3)＋Λ(4)＋Λ(5)＋Λ(6)＋Λ(7)＋Λ(8)＋Λ(9)

　　　　＝0＋log2＋log3＋log2＋log5＋0＋log7＋log2＋log3

　　Ψ^*(9)＝log2＋log3＋log2＋log5＋log7＋log2＋1/2・log3

となります。ｘが素数のべき乗でない場合は、両関数は等しくなります。例えば

　　Ψ(1000)＝Ψ(997)＝Ψ^*(1000)

に注意して下さい。

ゼ－タ関数ζ(s)

・ζ(s)＝Σ_n＝1～∞ 1/n^s＝Π_p∊P [1－1/p^s]^－1

に関して、

　ζ'(s)/ζ(s)＝－Σ_n＝1～∞ Λ(n)/n^s

となることを示します。

　ζ'(s)/ζ(s)＝(logζ(s))’＝－(Σ_p∊P log [1－1/p^s])’

です。ここで、テーラ－展開

　log(1－x)＝－Σ_n＝1～∞(xⁿ/n)

を用いると、

　log [1－1/p^s]＝－Σ_n＝1～∞(p^－ns／n)

なので、ｓで微分すると

　ζ'(s)/ζ(s)＝(logζ(s))’＝Σ_p∊PΣ_n＝1～∞ (p^－ns／n)’

となります。ここで

　(p^－ns／n)’＝ (e^{－nslog p}／n)’＝－nlog p・p^－ns／n＝－log p・p^－ns

に注意すると、

　－ζ'(s)/ζ(s)＝Σ_p∊PΣ_n＝1～∞log p・p^－ns

　　　　　＝Σ_p∊P (log p／p^s＋log p／p^2s＋log p／p^3s＋log p／p^4s＋・・・)

　　　　　＝log 2／2^s＋log 3／3^s＋log 5／5^s＋log 7／7^s＋・・・

            　　　＋log 2／2^2s ＋log 3／3^2s＋log 5／5^2s＋log 7／7^2s＋・・・

　　　　　　＋log 2／2^3s＋log 3／3^3s＋log 5／5^3s＋log 7／7^3s＋・・・

　　　　　　＋log 2／2^4s＋log 3／3^4s＋log 5／5^4s＋log 7／7^4s＋・・・

　　　　　＝log 2／2^s＋log 3／3^s＋log 2／4^s＋log 5／5^s＋log 7／7^s＋log 2／8^s

　　　　　　＋log 3／9^s＋log 11／11^s＋log 13／13^s ＋log 2／16^s＋・・・

　　　　　＝Σ_n＝1～∞ Λ(n)/n^s

が得られました。一般に

　D(s)＝Σ_n＝1～∞ a_n/n^s

なる級数をディリクレ級数（Series）といいます。同じ数列a_nに対する階段関数を

　S(x)＝Σ^*_n≦x a_n

とします。ここでΣ^*はステップアップ部分は中点をとることを意味します。D(s)とS(x)はペロンの公式で結び付けられています。

＜ペロンの公式＞

D(s)＝Σ_n＝1～∞ a_n/n^sがRe(s)＞1で絶対収束するとき、c＞1に対して、

　S(x)＝1/2πi・∫_{[c－i∞、c＋i∞]} D(s)x^s/s ds

が成り立つ。これを示します。

Re(s)＞0において、

　s∫_[n,∞] x^－s－1dx＝s[x^－s /(－s)] _[n,∞]＝1/n^s

が成り立ちます。するとディリクレ級数D(s)はRe(s)＞1で絶対収束しており、

　D(s)＝Σ_n＝1～∞ a_n/n^s＝sΣ_n＝1～∞∫_[n,∞] a_n x^－s－1dx

　　　＝s(∫_[1,∞] a₁ x^－s－1dx＋∫_[2,∞] a₂ x^－s－1dx＋∫_[3,∞] a₃ x^－s－1dx＋・・・)

　　　＝s(∫_[1,2] a₁ x^－s－1dx＋∫_[2,3] (a₁＋a₂) x^－s－1dx＋∫_[3,4] (a₁＋a₂＋a₃) x^－s－1dx＋・・・)

　　　＝s・∫_[0,∞] S(x)x^－s－1dx

となります。

ここで関数f(x)に対するメリン変換M_f(s)を

　　M_f(s)＝∫_[0,∞] f(x)x^s－1dx

と定義します。すると

　D(s)/s＝M_S(－s)

と表せます。逆メリン変換M^－1[・]

　M^－1[M_f(s)] (x)＝1/2πi・∫_{[c－i∞、c＋i∞]} M_f(s)x^－s ds＝f(x)

を用いると、f(x)をS(x)に置き換えて

　S(x)＝1/2πi・∫_{[c－i∞、c＋i∞]} M_S(s)・x^－s ds

　　　＝1/2πi・∫_{[c－i∞、c＋i∞]} M_S(－s)・x^s ds

　　　＝1/2πi・∫_{[c－i∞、c＋i∞]} D(s)/s・x^s ds

が得られました。結局

　－ζ'(s)/ζ(s)＝Σ_n＝1～∞ Λ(n)/n^s＝D(s)

a_n＝Λ(n)のときのディリクレ級数D(s)になります。

Λ(n)に対する階段関数はΨ^*(x)でした。

　S(x)＝Σ^*_n≦x a_n＝Σ^*_n≦xΛ(n)＝Ψ^*(x)

よって、ペロンの公式より、c＞1に対して

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} ζ'(s)/ζ(s)・x^s/s ds

が成り立ちます。　次回はこの複素積分を実行し、マンゴルトの明示公式を導出します。

複素平面全体で正則な関数を整関数といいます。R＞0に対して、整関数f(x)の最大値を

　M(R)＝max _{[｜z｜≦R]}｜f(z)｜

位数pを

　p＝lim sup _[R→∞] loglog M(R) / logR

とします。すなわちｐは

　max _{[｜z｜≦R]}｜f(z)｜≦exp(R^p＋ε)

が成り立つｐの内で最小のものです。

＜アダマ－ルの積定理＞

整関数f(x)の位数pが有限とする。Z＝0をm₀位の零点とする。他の零点をa1、a2、a3、・・・とし、その位数をm1、m2、m 3、・・・とする。このときｐ次以下の多項式g(z)が存在して、

　f(z)＝z^m0 e^g(z) Π_n=[1～∞] E(z/a_n,p)^m_n

と表せる。ここで

　E(z,0)＝1－z、

　E(z,1)＝(1－z) exp(z)

E(z,p)＝(1－z) exp(z＋z²/2＋z³/3＋・・・＋z^p/p)　ｐ＞1

である。

例えば、整関数f(z)＝sin(πz)の場合、位数p＝1、すなわち

　max _{[｜z｜≦R]}｜sin(πz)｜≦exp(R^1＋ε)

　e^iπz＝e^iπ(－iR)＝e^πRより、

　｜sin(πz)｜＝1/2・｜e^iπz＋e^－iπz｜＜1/2・｜e^πR＋e^－πR｜＜e^π・e^R

です。sin(πz)＝0　なるzは整数全体で、z→nで

　sin(πz)/ (z－n)＝(－1)ⁿ・sin(π(z－n)) / (z－n)　→　(－1)ⁿ

なので、全て1位の零点を有します。n∊Zに対して

　a_n＝n、m₀＝1、m_n＝1、g(z)＝az＋b

です。n≠0で

　sin(πz)＝z¹・exp(az＋b)・Π’_{n=[－∞～∞]} E(z/n,1)¹ 　　(n≠0)

　E(z,1)＝(1－z) exp(z)

だから、

sin(πz)＝z・exp(az＋b)・Π’_{n=[－∞～∞]} (1－z/n) exp(z/n)

　　　＝z・exp(az＋b)・Π_n=[1～∞] (1＋z/n) exp(－z/n) (1－z/n) exp(z/n)

　　　＝z・exp(az＋b)・Π_n=[1～∞] (1－z²/n²)

対数微分をとれば

　π・cos(πz)/ sin(πz)＝1/z＋a＋Σ_n=[1～∞]2z/ (z²－n²)

となります。すべて奇関数なので、a＝0となります。C＝e^bと置くと

　sin(πz)＝Cz・Π_n=[1～∞] (1－z²/n²)

　C＝lim_[z→0] π・sin(πz)／πz／Π_n=[1～∞] (1－z²/n²)＝π

よって

　sin(πz)＝πz・Π_n=[1～∞] (1－z²/n²)

が得られます。確かにz＝0、±nのときに零点になっています。

上式を展開すると

　sin(πz)＝πz－1/6・(πz)³＋1/5！・(πz)⁵＋・・・

　　　　＝πz・(1－Σ_n=[1～∞] z²/n²＋Σ_n>m≧1 z⁴/n² m²＋・・・)

z³の係数を較べて、

　－π³/6＝－πΣ_n=[1～∞] /n²＝－πζ(2)

　　ζ(2) ＝π²/6

が得られます。同様にz⁵の係数を較べて、

　π⁵/120＝πΣ_n>m≧1 z⁴/n² m²

　ζ(2) ²＝[Σ_n=[1～∞] 1 /n²]・[Σ_m=[1～∞]1 /m²]

　　　＝Σ_m=[1～∞] 1 /n⁴＋2Σ_n>m≧1 z⁴/n² m²

　(π²/6) ²＝ζ(4)＋2・π⁴/120

　ζ(4)＝π⁴/36－π⁴/60＝π⁴ (5/180－3/180)＝π⁴/90

が得られます。

＜ガンマ関数の積表示＞

ガンマ関数1/Γ(z)は整関数で、0以下の整数が位数1の零点でした。アダマ－ルの積定理より、

　1/Γ(z)＝ze^az＋bΠ_n=[1～∞] (1＋z/n) exp(－z/n)

よって

　1/zΓ(z)＝1/Γ(z＋1)＝e^az＋bΠ_n=[1～∞] (1＋z/n) exp(－z/n)

ここでz＝0とおくと

　1＝1/Γ(0＋1)＝e^a0＋bΠ_n=[1～∞] (1＋0/n) exp(－0/n)＝e^b

よって

　1/Γ(z)＝ze^azΠ_n=[1～∞] (1＋z/n) exp(－z/n)

ここでz＝1とおくと

　1/Γ(1)＝1e^aΠ_n=[1～∞] (1＋1/n) exp(－1/n)

対数をとって

　0＝ａ＋Σ_n=[1～∞][ log(1＋1/n)－1/n]

aの値は

　a＝lim_N→∞Σ_n=[1～N][ 1/n－log(n＋1)－logn)]

　　＝lim_N→∞　Σ_n=[1～N](1/n)－log(N＋1)

　　＝lim_N→∞　Σ_n=[1～N](1/n)－logN＋log(N/ (N＋1))

　　＝lim_N→∞　Σ_n=[1～N](1/n)－logN

　　＝γ

となります。γはオイラ－の定数と呼ばれる値で、γ＝0.57721・・・です。従って

　1/Γ(z)＝ze^γzΠ_n=[1～∞] (1＋z/n) exp(－z/n)

　1/Γ(－z)＝－ze^－γzΠ_n=[1～∞] (1－z/n) exp(＋z/n)

です。Γ(1－z)＝－zΓ(－z)より

　1/Γ(z)Γ(1－z)

＝－1／zΓ(z)Γ(－z)

＝1/z・ze^γzΠ_n=[1～∞] (1＋z/n) exp(－z/n)・ze^－γzΠ_n=[1～∞] (1－z/n) exp(＋z/n)

＝zΠ_n=[1～∞] (1＋z/n) (1－z/n)

＝zΠ_n=[1～∞] (1－z²/n²)

＝sin(πz)/π

となり、相反定理が得られます。

 

＜ゼ－タ関数の関数等式とテータ関数の関係＞

ゼ－タ関数の関数等式は

　ξ(x)＝π^－s/2Γ(s/2)ζ(s)

とおくと

　ξ(x)＝ξ(1－x)

で表されます。テータ関数

　θ(t)＝Σ_{n＝[－∞、∞]} e^{－πtn^2}

の変換公式は

　θ(t)＝θ(1/t)/√t

でした。

　Ψ(t)＝Σ_{n＝[1、∞]} e^{－πtn^2}

とおくと、

　θ(t)＝1＋2Ψ(t)

が成り立ちます。Γ関数の定義において、

　Γ(s)＝∫_[0、∞] x^s－1e^－xdx　(s＞0)

x＝πtn²と変数変換すると、dx＝πn²dtとなり

　Γ(s)＝∫_[0、∞] (πtn²)^s－1e^{－πtn^2}πn² dt

　　　＝π^sn^2s∫_[0、∞] t^s－1e^{－πtn^2} dt

なので

　Γ(s/2)＝π^s/2n^s∫_[0、∞] t^s/2－1e^{－πtn^2}dt

両辺をπ^s/2n^sで割って

　π^－s/2・1/n^s Γ(s/2)＝∫_[0、∞] t^s/2－1e^{－πtn^2} dt

これを全ての自然数nについて加えれば

　π^－s/2・Γ(s/2) [Σ_{n＝[1、∞]} 1/n^s]＝∫_[0、∞] t^s/2－1[Σ_{n＝[1、∞]} e^{－πtn^2}]dt

　π^－s/2・Γ(s/2)ζ(s) ＝∫_[0、∞] t^s/2－1Ψ(t) dt

を得ます。　

　右辺＝∫_[0、1] t^s/2－1Ψ(t) dt＋∫_[1、∞] t^s/2－1Ψ(t) dt

として、第一項で、t＝1/uと変数変換すると、dt＝－1/u² duより

　∫_[0、1] t^s/2－1Ψ(t) dt＝－∫_[∞、1] (1/u)^s/2－1Ψ(1/u) 1/u² du

 　　　　　　　　　　＝∫_[1、∞] u^－s/2－1Ψ(1/u) du

ここで

　　1＋2Ψ(u)＝θ(u)＝θ(1/u)/u^1/2＝[1＋2Ψ(1/u)]/u^1/2

となることから、

　Ψ(1/u)＝u^1/2Ψ(u)＋1/2・u^1/2－1/2

を得ます。これを代入すると

　∫_[0、1] t^s/2－1Ψ(t) dt

　＝∫_[1、∞] u^－s/2－1[u^1/2Ψ(u)＋1/2・u^1/2－1/2]du

　＝∫_[1、∞] u^{(1－s)/2－1}Ψ(u) du ＋1/2∫_[1、∞] u^{(1－s)/2－1} du－1/2∫_[1、∞] u^－s/2－1du

　＝∫_[1、∞] u^{(1－s)/2－1}Ψ(u) du ＋1/(s－1)－1/s

　＝∫_[1、∞] u^{(1－s)/2－1}Ψ(u) du －1／s(1－s)

となります。なぜなら、s>0より

　1/2∫_[1、∞] u^{(1－s)/2－1}du＝1/2・2/(1－s) [u^(1－s)/2]_u＝1、∞＝1/(s－1)　

　－1/2∫_[1、∞] u^－s/2－1du＝－1/2・(－2/s)[u^－s/2]_u＝1、∞＝－1/s

よって

　右辺＝∫_[0、1] t^s/2－1Ψ(t) dt＋∫_[1、∞] t^s/2－1Ψ(t) dt

　　　＝∫_[1、∞] u^{(1－s)/2－1}Ψ(u) du －1／s(1－s)＋∫_[1、∞] t^s/2－1Ψ(t) dt

　　　＝∫_[1、∞] [u^{(1－s)/2－1}＋u^s/2－1]Ψ(u) du －1／s(1－s)

となります。右辺は全ての実数sに対して積分が存在し、sを1－sに置き換えても、式が変わりません。

　左辺：ξ(s)＝π^－s/2・Γ(s/2)ζ(s)

とすると、

　ξ(s)＋1／s(1－s)＝∫_[1、∞] [t^{(1－s)/2－1}＋t^s/2－1]Ψ(t) dt

は全ての実数sで定義され、関数等式

　ξ(s)＝ξ(1－s)

が成り立ちます。

 

＜ζ’(0)の計算＞

ここでは

　ζ’(0)＝－1/2・log(2π)

を示します。

複素数sに対して、イ－タ関数

　η(s)＝1－1/2^s＋1/3^s－1/4^s＋・・・

はRe(s)＞0で収束し、この範囲で正則です。

イ－タ関数は

　｜η(s)｜＝｜1－1/2^s＋1/3^s－1/4^s＋・・｜≦1＋1/2^s＋1/3^s＋1/4^s＋・・＝ζ(s)

よりRe(s)＞1で収束することは明らかです。

イ－タ関数とゼ－タ関数には

　η(s)＝(1－2^1－s)ζ(s)

なる関係がありました。

　Lim_[s→1] η(s)＝Lim_[s→1] (1－2^1－s)/(s－1)・(s－1)ζ(s)

　　　　　＝Lim_[t→0] (2⁰－2^－t)/t・Lim_[s→1] (s－1)ζ(s)

　　　　　＝－Lim_[t→0] (2⁰－2^－t)/(0－t)・1

　　　　　＝Lim_[t→0] (－2^－t)’

　　　　　＝log2

ここで

　(－2^－t)’＝ (－e^－tlog2)’ ＝ log2 (e^－tlog2)＝log2・2^－t

を用いました。つまりs＝1はη(s)の除去可能な特異点であり、η(s)はs＝1で正則です。

ここでイ－タ関数の部分和

　η_N(s)＝Σ_n＝1～N　(－1)^n－1/n^s

を考えると　

　η_2＜η_4＜η_{6＜・・＜}η_2N＜η_2N＋2＜η_2N＋1＜η_{2N－1＜・・＜}η_5＜η_3＜η₁

なので、Re(s)＞0ならば

　Lim_[N→∞] (η_2N－η_2N－1)＝－Lim_[N→∞]1/(2N)^S＝0

だから

　Lim_[N→∞] η_2N＝Lim_[N→∞]η_2N－1＝η(s)

となります。イ－タ関数η(s)はRe(s)＞0で収束し、この範囲で正則です。

先ほどの関係式

　η(s)＝(1－2^1－s)ζ(s)

の両辺を微分すると

　η’(s)＝log2・2^1－sζ(s)＋(1－2^1－s)ζ’(s)

となります。s＝0を代入すると

η’(0)＝log2・2^1－0ζ(0)＋(1－2^1－0)

　　　＝log2・2・(－1/2)－ζ’(0)

　　　＝－log2－ζ’(0)

が得られます。η’(0)を求めるために、η(s)を変形すると

η(s)＝1－1/2^s＋1/3^s－1/4^s＋・・・

　　＝1/2[1+1－1/2^s－1/2^s＋1/3^s＋1/3^s－1/4^s－1/4^s＋・・・]

　　＝1/2+1/2 [(1－1/2^s)－(1/2^s－1/3^s)＋(1/3^s－1/4^s)－(1/4^s－1/5^s)＋・・・]

η(s)は全複素平面で正則なため、両辺を微分すると

　η’(s)＝1/2 [(0＋log2/2^s)－(－log2/2^s＋log 3/3^s)＋(－log 3/3^s＋log4/4^s)－(－log4/4^s＋log5/5^s)＋・・・]

となります。この右辺はRe(s)＞0の範囲で広義一様収束していることから、ｓ→＋0の極限をとると、

　η’(0)＝1/2 [log2－(－log2＋log 3)＋(－log 3＋log4)－(－log4＋log5)＋・・・]

　　　＝1/2・log(2/1・2/3・4/3・4/5・・・)

　　　＝1/2・log(π/2)

となります。ここでウォリスの公式を用いました。従って

　　　ζ’(0)＝－η’(0) －log2

　　　　　　＝－1/2・log(π/2) －1/2・log4

　　　　　　＝－1/2・log(2π)

が得られます。

 　η(0)＝(1－2^1－0)ζ(0)＝－1(－1/2)＝1/2

ですから、まとめると

　ζ(0)＝－1/2、ζ’(0)＝－1/2・log(2π)

　η(0)＝＋1/2、η’(0)＝＋1/2・log(π/2)

が成り立ちます。

＜ガンマ関数の解析接続＞

Γ関数は

　Γ(s)＝∫_[0、∞] t^s－1e^－tdt

で定義されています。sを複素数に拡張した場合に、区間[0、∞]での積分は収束するか調べて見ましょう。

s＝x＋iyとして、0＜x₀＜x₁なる任意の実数を用いて、0＜x₀＜x＜x₁とすれば、

　  Γ(s)＝∫_[0、1] t^s－1e^－tdt＋∫_[1、∞] t^s－1e^－tdt

　｜Γ(s)｜≦ ∫_[0、1] ｜t^s－1｜e^－tdt ＋ ∫_[1、∞] ｜t^s－1｜e^－tdt

であり、

　(1/2)^x＜(1/2)^x0　、2^x＜(2)^x1

に注意すると、

∫_[0、1] ｜t^s－1｜e^－tdt＝∫_[0、1] t ^x－1e^－tdt≦∫_[0、1] t ^x0－1e^－tdt≦∫_[0、∞] t ^x0－1e^－tdt＝Γ(x₀)

∫_[1、∞] ｜t^s－1｜e^－tdt＝∫_[1、∞] t ^x－1e^－tdt≦∫_[1、∞] t ^x1－1e^－tdt≦∫_[0、∞] t ^x1－1e^－tdt＝Γ(x₁)

ですから、

｜Γ(s)｜≦Γ(x₀)＋Γ(x₁)

が成り立ちます。従って0＜x₀＜Re(s)＜x₁において、ε→0のとき

　Γ_ε(s)＝∫_[ε、1/ε] t^s－1e^－tdt　→　Γ(s)＝∫_[0、∞] t^s－1e^－tdt　

となり、Γ_ε(s)はΓ(s)に一様収束します。Γ_ε(s)は有限区間での積分だから、sの正則関数です。

一様収束極限であるΓ(s)もx₀＜Re(s)＜x₁における正則関数です。x₀、x₁は任意だから、

Γ(s)はRe(s)＞0におけるsの正則関数になっています。nを任意の自然数とすれば、

　Γ(s)＝Γ(s＋n)／s(s＋1) (s＋2)・・ (s＋n－2) (s＋n－1)

が成り立ちます。Γ(s)はRe(s)＋n＞0における有理型関数で、s＝0,－1,－2,・・・－n+1でを1位の極とする以外は、正則になっています。nは任意なので、Γ(s)は複素数全体で正則な有理型関数で、s＝0,－1,－2,・・・で1位の極をもっています。Γ(1－s)は、s＝0,1,2,・・・で1位の極をもっています。さらに整数でない実数sに対して

　Γ(s)Γ(1－s)＝π/sin(πs)

が成り立ちます。複素関数論の一致の定理より、整数でない複素数に関して、この等式は成り立っています。この等式から、ガンマ関するΓ(s)は零点を持たない有理型関数であることが分かります。よって1/Γ(s)は複素数全体で正則な関数になっています。

＜リ－マン関数等式からオイラ－関数等式の導出＞

関数等式には、非対称型のオイラ－による関数等式

　ζ(1－s)=cos(sπ/2) Γ(s)ζ(s)／2^s－1π^s・・・・（1）

と対称型のリ－マンによる関数等式

　π^－s/2Γ(s/2)ζ(s)＝π^－(1－s)/2Γ((1－s)/2)ζ(1－s) ・・・・（2）

がありました。これまでオイラ－による関数等式からリ－マンによる関数等式を導出しました。今度は逆にリ－マンによる関数等式からオイラ－による関数等式を導出します。

(2)の両辺に(－s)Γ(－s/2)を掛けると、

　π^－s/2(－s)Γ(－s/2)Γ(s/2)ζ(s)＝π^－(1－s)/2(－s)Γ(－s/2)Γ((1－s)/2)ζ(1－s)

左辺の係数は

　π^－s/2 2(－s/2)Γ(－s/2)Γ(s/2)＝2π^－s/2Γ(1－s/2)Γ(s/2)＝π^－s/2 2π/ sin(πs/2)

となります。ここで、ガンマ関数の相反公式：Γ(s/2)Γ(1－s/2)＝π/sin(πs/2)を用いました。ルジャンドルの2倍公式

　Γ(2s)＝2^2s－1/π^1/2・Γ(s) Γ(s+1/2)

でs→－s/2に置き換えた

　Γ(－s)2^s+1π^1/2＝Γ(－s/2) Γ((1－s)/2)

を用いると、右辺の係数は

　π^－(1－s)/2 (－s)Γ(－s/2)Γ((1－s)/2)＝π^－(1－s)/2 (－s)Γ(－s) 2^s+1π^1/2

　　＝2^s+1π^s/2Γ(1－s)

となります。従って、左辺＝右辺は

　π^－s/22π/ sin(πs/2)ζ(s)＝2^s+1π^s/2Γ(1－s)ζ(1－s)

となります。

　ζ(s)＝2^sπ^s－1Γ(1－s)ζ(1－s) sin(πs/2) ・・・・（*）

が得られます。s→1－sに置き換えると

　sin(π(1－s) /2)＝sin(π/2)cos(－πs/2)＝cos(πs/2)

より

　ζ(1－s)＝Γ(s)ζ(s) cos(πs/2)／2^s－1π^s・・・・（1）

が得られます。

＜ゼ－タ関数の自明な零点はs＝－2k＞

　ζ(s)＝2^sπ^s－1Γ(1－s)ζ(1－s) sin(πs/2) ・・・・（*）

ζ(1－s)は1－s＞1、すなわち、s＜0で定義されています。

　sin(πs/2)＝0　→　s＝－2、－4、－6、・・－2k、・・・

なる負の偶数では

　ζ(－2k)＝0　for　k＝1、2、3・・・

が成り立ちます。これをζ(s) の自明な零点と言います。

また、この公式からζ(0)の値が得られます。

lim_[s→1] (s－1)ζ(s)＝1　→　lim_[s→0] ((1－s)－1)ζ(1－s)＝1

に注意すると

ζ(0)＝lim_[s→0] 2^sπ^s－1Γ(1－s)ζ(1－s) sin(πs/2)

　　　＝－1/2・Γ(1) lim_[s→0]sin(πs/2)/(πs/2)・(1－s－1)ζ(1－s)

　　　＝－1/2

となります。

 

＜ルジャンドルの2倍公式の証明＞

　Γ(2s)＝2^2s-1/π^1/2・Γ(s) Γ(s+1/2)

を証明する。

今、B(x,y)＝Γ(x)Γ(y)/Γ(x＋y) より

　B(x,1/2)＝Γ(x)Γ(1/2)/Γ(x+1/2)

　B(x,x)＝Γ(x)² /Γ(2x)

が成り立つ。先ほど証明された式

　B(x,1/2)＝2^2x－1B(x,x)

に代入すると、

　Γ(x)Γ(1/2)/Γ(x+1/2)＝2^2x－1Γ(x)² /Γ(2x)

を得る。Γ(1/2)＝π^1/2より

　Γ(2x)＝2^2x－1π^－1/2Γ(x)Γ(x+1/2)

が成り立つことが示された。

Γ(n)=(n-1)!　、Γ(1/2)=π^－1/2なので、ｘ＝4のとき

Γ(8)＝2^2*4－1π^－1/2Γ(4)Γ(4+1/2)＝2³Γ(4)・2⁴Γ(4+1/2)π^－1/2

2⁴Γ(4+1/2)π^－1/2＝2⁴・7/2 Γ(7/2)π^－1/2＝2⁴・7/2・5/2・3/2・1/2 Γ(1/2)π^－1/2

　　　　　　　＝7・5・3・1

2³Γ(4)＝2³（3・2・1）＝6・4・2

Γ(8)＝7！＝7・5・3・1・6・4・2

を表しています。

＜ガンマ関数の相反公式＞

　Γ(x)Γ(1－x)＝π/sin(πx)

を証明します。その前にこの公式の直感的な説明をします。

Γ(x)はｘ＝0，-1，-2，・・・でのみ1位の極をもちます。Γ(1-x)はｘ＝1，2，3，・・・でのみ1位の極をもちます。

f(x)=1/Γ(x)Γ(1－x)は全ての整数で1位の零点をもちます。ｘをｘ+1にすると

　Γ(ｘ+1)Γ(1-（ｘ+1））＝ｘΓ(ｘ)Γ(-ｘ）＝-ｘΓ(ｘ)Γ(1-ｘ）

ので、f(x+2)＝－f(x+1)＝f(x)　となり、f(x)は周期2の関数であることが分かります。ｘ＝1/2で最大値

　f(1/2)＝1/Γ(1/2)Γ(1－1/2)＝1/π

をとります。よってf(x)＝sin(πx)/πと予想できます。

証明に入ります。先ほどもとめたベータ関数の性質は

（4）：B(x,1－x)＝∫_[0，∞] u^x－1/(1＋u) du

（5）：B(x,1－x)＝Γ(x)Γ(1－x)

ですから、

　∫_[0，∞] x^a－1/(1＋x) dx＝π/sin(πa)　0＜a＜1

を示せばよいことが分かります。

D積分閉路を使って

　f(z)＝z^a－1/(1＋z)

の複素積分を行います。D積分閉路は

　D＝C₁＋C₂(ε)＋C₃＋C_R

からなります。

 

 

 

 

 

ε→0、R→∞で

　∫_C2(ε)f(z)dz→0、∫_CR f(z)dz→0

となります。0＜a＜1より、－1＜a－1＜0、に注意すると

　－ε+1≦εe^iθ+1≦ε+1より、1/｜(εe^iθ＋1)｜≦1/(1－ε)

なので、z＝εe^iθ、dz＝iεe^iθdθ、0＜a＜1、より

　｜∫_C2(ε)f(z)dz｜≦∫_[0、2π]｜(εe^iθ) ^a－1｜/｜εe^iθ＋1｜｜iεe^iθ｜dθ

　　　　　　　≦εε^a－1/(1－ε) 2π＝2πε^a/(1－ε)　→　0　as　ε→0

同様に、－1＜a－1＜0、より

　｜∫_CRf(z)dz｜≦∫_[0、2π]｜(Re^iθ) ^a－1｜/｜Re^iθ＋1｜｜iRe^iθ｜dθ

　　　　　　　≦2πR・R^a－1/R＝2πR^a－1→　0　as　R→∞

となります。

z ^a－1はz＝0で特異点を持ちますが、z＝0は経路D内には含まれません。

D積分閉路内の極は、z＝－1だけです。f(z)のz＝－1での留数は

　Res[f,－1]＝lim_[x→－1] (z＋1) z ^a－1/(z＋1)＝(e^iπ) ^a－1＝e^iπa e^－iπ＝－e^iπa

　∫_D f(z)dz＝2πi Res[f,－1]＝2πi (－e^iπa)

となります。

C₃上での偏角は0だからz＝xe⁰代入して、ε→0、R→∞で

　∫_C3 f(z)dz＝∫_[ε、R] x^a－1/(1＋x) dx　→　I＝∫_[0、∞] x^a－1/(1＋x) dx

C₁上での偏角は2πなので、z＝xe^2πi代入して、ε→0、R→∞で

　z^a－1＝(xe^2πi) ^a－1＝x ^a－1e^2πiae^－2πi＝x ^a－1e^2πia

　∫_C1 f(z)dz＝∫_[R、ε] e^2πia x^a－1/(1＋x) dx　→∫_[0、∞] x^a－1/(1＋x) dx

となります。従って

　2πi (－e^iπa)＝I＋0＋I＋0＝(1－e^2πia)I

これをIについて解くと

　I＝2πi (－e^iπa)/ (1－e^2πia)＝2πi (－e^iπa)／(－e^iπa) (e^iπa－e^－iπa)

　　＝π/sin(πa)

が得られます。

 

ゼ－タ関数とガンマ関数とベータ関数は相互に密接な関係があります。ここではベータ関数のいくつかの性質を紹介します。これらはルジャンドルの倍公式やガンマ関数の相反公式を証明するのに役立ちます。

＜ベ－タ関数の諸性質＞

ベ－タ関数は

　B(x,y)＝∫_[0，1] t^x－1(1－t)^y－1dt  (x>0,y>0)

で定義されます。

（1）B(x,y)＝B(y,x)

　t’＝1－tとおくと、

B(x,y)＝－∫_[1，0] (1－t’)^x－1 t’^y－1dt’ ＝B(y,x)

（2）B(x,y)＝2∫_[0，π/2] sin^2x－1θcos^2y－1θdθ

　　t＝sin²θとおくと、dt＝2sinθcosθdθ

　　B(x,y)＝∫_[0，π/2] (sin²θ)^x－1(cos²θ)^y－12sinθcosθdθ

　　　　＝2∫_[0，π/2] sin^2x－1θcos^2y－1θdθ

（3）B(x,y)＝Γ(x)Γ(y) /Γ(x＋y)

　　t＝s²とおくと、dt＝2sdsより

　　Γ(x)＝∫_[0，∞] t^x－1 e^－t dt＝2∫_[0，∞] s^2x－1 e^－ss ds

　　Γ(x)Γ(y)＝4∫_[0，∞] t^2x－1 e^－tt dt・∫_[0，∞] s^2y－1 e^－ss ds

　　t＝rcosθ、s＝rsinθとおくと、t²＋s²＝r²、dtds＝rdrdθ

　　4∫_[0，π/2]dθ∫_[0，∞] dr (rcosθ)^2x－1 (rsinθ)^2y－1 e^－rr

　＝2∫_[0，π/2]dθ∫_[0，∞] dr cos^2x－1θsin^2y－1θ・2∫_[0，∞] r^2(x＋y)－2e^－rr rdr

　t＝r²とおくと、dt＝2rdrより、r^2(x＋y)－2＝t^(x＋y)/r²＝t^(x＋y)－1

　　Γ(x)Γ(y)＝B(x,y)・∫_[0，∞] t^(x＋y)－1e^－t dt＝B(x,y)・Γ(x＋y)

が示された。

（4）B(x,y)＝∫_[0，∞] u^x－1/(1＋u)^x＋y du

　　B(x,y)＝∫_[0，1] t^x－1(1－t)^y－1dt 

　において、t＝u/(1＋u)とおくと　

　　1－t＝1－u/(1＋u)＝1/(1＋u)

　(1＋u)t＝u、u－ut＝t、u＝t/(1－t)　→u＝0～∞
　du＝[(1－t)+t]/(1－t)² dt＝1/(1－t)² dt＝(1＋u) ² dt

　→　dt＝du/(1＋u) ²

であるから

　t^x－1(1－t)^y－1dt＝[u/(1＋u)]^x－1(1＋u)^－y＋1(1＋u)^－2du
＝u^x－1(1＋u)^－(x＋y) du

　B(x,y)＝∫_[0，∞] u^x－1(1＋u)^－(x＋y) du

が示された。

y＝1－xのとき

　B(x,1－x)＝∫_[0，∞] u^x－1(1＋u)^－(x＋y) du

　　　　　＝∫_[0，∞] u^x－1/(1＋u) du

が成り立つ。

（5）B(x,1－x)＝Γ(x)Γ(1－x)

　B(x,y)＝Γ(x)Γ(y)/Γ(x＋y) において

　　y＝1－xと置くと、Γ(x＋y)＝Γ(1)＝1より

　B(x,1－x)＝Γ(x)Γ(1－x)/Γ(1)＝Γ(x)Γ(1－x)

（6）B(x,1/2)＝2^2x－1B(x,x)

　B(x,1/2)＝B(1/2 ,x)＝∫_[0，1] t^－1/2 (1－t) ^x－1dt

　t＝u²とおくと、t^－1/2＝u^－1、dt＝2udu

　B(x,1/2)＝2∫_[0，1] (1－u²)^x－1 du

　　　　＝∫_[0，1] (1－u²)^x－1 du－∫_[0，－1] (1－u²)^x－1 d(－u)

　　　　＝∫_[0，1] (1－u²)^x－1 du＋∫_[－1，0] (1－u²)^x－1 du

　　　　＝∫_[－1，1] (1－u²)^x－1 du

　s＝(1+u)/2とおくと、u＝2s－1、s＝0～1

　　1－u＝1－2s+1＝2(1－s)

　　1－u²＝(1－u) (1＋u)＝4(1－s)s

　B(x,1/2)＝2∫_[0，1] (4(1－s)s)^x－1 2ds

　　　　＝2^2x－1∫_[0，1] (1－s) ^x－1s^x－1 ds

　　　　＝2^2x－1B(x,x)

が示された。

 

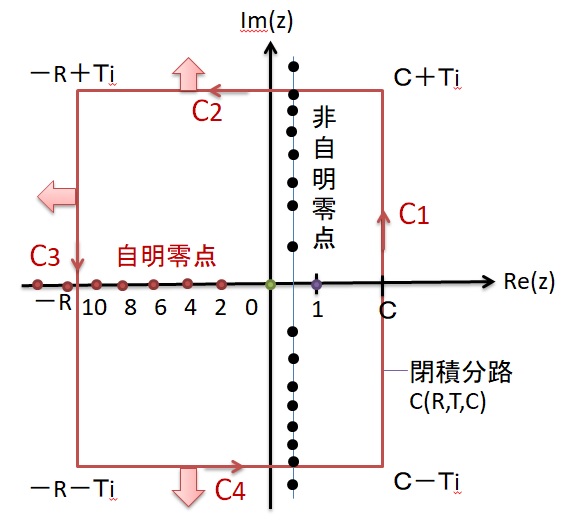
＜ゼ－タ関数の関数等式の証明＞

関数等式には、非対称型のオイラ－による関数等式

　ζ(1－s)=cos(sπ/2) Γ(s)ζ(s)／2^s－1π^s・・・・（1）

と対称型のリ－マンによる関数等式

　π^－s/2Γ(s/2)ζ(s)＝π^－(1－s)/2Γ((1－s)/2)ζ(1－s) ・・・・（2）

があります。関数等式はゼ－タ関数の定義域を拡大する場面でよく用いられす。

ここではオイラ－による関数等式を導出し、その後

ガンマ関数の相反公式

   Γ(s)Γ(1－s)＝π/sin(πs)

においてs→(1－s)/2に置き換えた

　Γ((1－s)/2)Γ((1＋s)/2)＝π/cos(πs/2)　　・・・（5）

の式とルジャンドルの2倍公式

　Γ(2s)＝2^2s-1/π^1/2・Γ(s) Γ(s+1/2)

においてs→s/2に置き換えた

　Γ(s)＝2^s-1/π^1/2・Γ(s/2) Γ((s+1)/2) 　・・・（6）

式を用いて、リ－マンによる関数等式を導出します。

その前に、ゼ－タ関数の積分表示を求めましょう。

＜ゼ－タ関数の積分表示＞

ゼ－タ関数：ζ(s)＝Σ_n＝1-∞ 1/n^s

ガンマ関数：Γ(s)＝∫_[0、∞] x^s－1e^－xdx

のとき、s＞1に対して

　∫_[0、∞] x^s－1/(e^x－1)dx=ζ(s) Γ(s)

が成り立つ。

[証明]

　1/(e^x－1)＝e^－x/(1－e^－x)＝Σ_n=1-∞ (e^－x)ⁿ ＝Σ_n=1-∞ e^{－n x}

を代入すると、

∫_[0、∞] x^s－1/(e^x＋1)dx=∫_[0、∞] x^s－1Σ_n=1-∞ e^{－n x} dx

                   =Σ_n=1-∞∫_[0、∞] x^s－1 e^{－n x} dx

ここで、y＝nx　と変数変換すると

　∫_[0、∞] x^s－1/(e^x＋1)dx =Σ_n=1-∞∫_[0、∞] (y/n)^s－1 e^－y dy/n

=Σ_n=1-∞1/n^s∫_[0、∞] y^s－1 e^－y dy

＝ζ(s)Γ(s)

が示されました。

＜オイラ－による関数等式の導出＞

複素積分
　I(s)＝∫_C z^s－1/(e^z－1)dz

を2つの積分経路で求めて、等値することで(1)式のオイラ－による関数等式を導出します。

1）ハンケル積分経路による積分計算

Cをハンケル積分経路とすると、全複素平面で

　∫_C z^s－1/(e^z－1)dz＝(e^2πsi－1) ζ(s)Γ(s)　　　・・・・（3）

が成立することを示します。

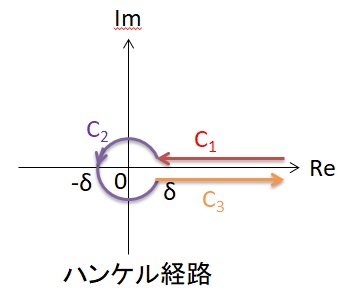
Ｃは以下の3つの経路

　C1：z＝x＋iε　x＝∞→r

　C2：z＝re^iθ　θ＝0→2π

　C3：z＝x－iε　x＝r→∞

から成ります。

　I(s)＝∫_C z^s－1/(e^z－1)dz

　　＝∫_C1 z^s－1/(e^z－1)dz＋∫_C2 z^s－1/(e^z－1)dz＋∫_C3 z^s－1/(e^z－1)dz

である。まず経路1での積分はε→0で

　I₁(s)＝∫_C1 z^s－1/(e^z－1)dz＝－∫_[0、∞] x^s－1/(e^x－1)dx

となる。経路2の積分はr→0で

｜I₂(s)｜＝｜∫_C2 z^s－1/(e^z－1)dz｜≦∫_[0，2π] r^s/[(e^r－1)/r]dθ≦r^s・2π→　0　as r→0  s＞0

ゼロになる。経路3では、原点の周りの1回転して位相2πが付加されるので

　z ^s－1＝(re^i2π) ^s－1＝r ^s－1e^i2πs

より、e^i2πsが残る。rをxに置き換えて0から∞まで積分すると、

　I₃(s)＝∫_C3 z^s－1/(e^z－1)dz＝e^i2πs∫_[0、∞] x^s－1/(e^x－1)dx

従って、ε→0、r→0の極限では、ゼ－タ関数の積分表示を用いて

　I(s)＝－∫_[0、∞] x^s－1/(e^x－1)dx＋　0　＋e^i2πs∫_[0、∞] x^s－1/(e^x－1)dx

　　　＝(e^i2πs－1) ∫_[0、∞] x^s－1/(e^x－1)dx

　　　＝(e^i2πs－1) ζ(s)Γ(s)

が示されました。

ここでs＝1のとき

　e^i2πs－1＝0

なので、s＝1は(e^i2πs－1)の1位の零点です。ζ(s)＝1/(s－1)+F(s)と書け、ζ(s)はs＝1で1位の極を持ちます。従って、(e^i2πs－1)ζ(s)はs＝1で正則になっています。上式は全ての複素数sで成り立っています。

 

2）D積分経路による積分計算

下図のように積分経路Dを取ります。全複素平面で

∫_C z^s－1/(e^z－1)dz＝－∫_D z^s－1/(e^z－1)dz＝(2π)^s(e^3πsi/2－e^πsi/2)ζ(1－s)　・・（4）

が成立することを示します。

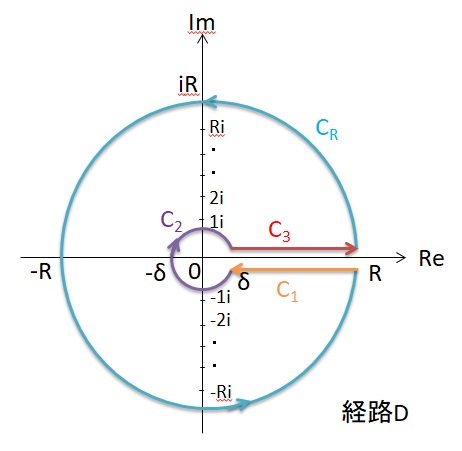
経路Dは

　D＝C₁＋C₂＋C₃＋C_R

から成ります。経路Dの4つの経路は

　C₁：z＝x－iε　x＝∞→r

　C₂：z＝re^iθ　θ＝2π→0

　C₃：z＝x＋iε　x＝∞→r

　C_R：z＝Re^iθ　θ＝0→2π

です。分母にe^zがあるのでC_Rに関する積分はR→∞でゼロになります。ところで

C₁＋C₂＋C₃の経路での積分は先ほどのハンケル積分経路と逆向きなので、

　∫_C z^s－1/(e^z－1)dz＝－∫_D z^s－1/(e^z－1)dz

となります。被積分関数の分母はz＝±2nπiでゼロになります。経路Dは、被積分関数の極、z＝±2πi、±4πi、±6πi、・・±2nπi（＜Ri）を含んでいます。従って経路Cでの積分は、経路D内の積分の留数の和を求めて、全体にマイナス符号をつければ得られます。

　z＝2nπiでの留数は、ｎ＞0のとき偏角はπ/2なので（i＝e^iπ/2)

　I_＋＝lim _[z→2nπi] (z－2nπi)・ z^s－1/(e^z－1)
　　＝lim _[z→2nπi]・ z^s－1／(e^z－e^2nπi )/
　　＝lim _[z→2nπi]・ z／(e^z)’

　　＝(2nπi) ^s－1

　　＝(2nπ) ^s－1(e^iπ/2) ^s－1

　　＝－i・(2nπ) ^s－1・e^iπs/2

となります。

　z＝－2nπiでの留数は、偏角は3π/2なので、（－i＝e^i3π/2)

I_－＝(－2nπi) ^s－1

　＝(2nπ) ^s－1(e^i3π/2) ^s－1

　＝i・(2nπ) ^s－1・e^i3πs/2

となります。R→∞のとき、ｎ＝1～∞の全ての留数の和を求めると、

　∫_D z^s－1/(e^z－1)dz＝Σ_n 2πi・(I_＋＋I_－)

　　　　　　　　　＝Σ_n 2πi[－i・(2nπ) ^s－1・(e^iπs/2－e^i3πs/2)]
　　　　　　　　　＝(2π) ^s(e^iπs/2－e^i3πs/2)・Σ_n 1/n ^1－s

　             　　　　 ＝(2π) ^s(e^iπs/2－e^i3πs/2)・ζ(1－s)

従って、

    ∫_C z^s－1/(e^z－1)dz＝(2π) ^s(e^i3πs/2－e^iπs/2)ζ(1－s)

が示されました。

＜オイラ－による関数等式の導出＞

2つの積分経路で求めた

   I(s)＝∫_C z^s－1/(e^z－1)dz

の値を等値することで、オイラ－による関数等式（非対称型）

　ζ(1－s)=cos(sπ/2) Γ(s)ζ(s)／2^s－1π^s・・・・（1）

を導出します。

2つの積分経路で求めた値は
　∫_C z^s－1/(e^z－1)dz＝(e^2πsi－1) ζ(s)Γ(s)　　・・・（3）

   ∫_C z^s－1/(e^z－1)dz＝－∫_D z^s－1/(e^z－1)dz＝(2π)s(e^3πsi/2－e^πsi/2) ζ(1－s)　・・（4）

でした。よって

   (e^2πsi－1) ζ(s)Γ(s)＝(2π)^s(e^3πsi/2－e^πsi/2) ζ(1－s)　

が成り立ちます。

　(e^2πsi－1)/ (e^3πsi/2－e^πsi/2)＝e^πsi(e^πsi－e^－πsi) / e^πsi (e^πsi/2－e^－πsi/2)

　＝(e^πsi/2＋e^－πsi/2) (e^πsi/2－e^－πsi/2) / (e^πsi/2－e^－πsi/2)

　＝2cos(πs/2)

ですから、

　2cos(πs/2)ζ(s)Γ(s)＝(2π)^sζ(1－s)　

よって

　ζ(1－s)＝2cos(πs/2)Γ(s)/ (2π)^s・ζ(s)

　　　　＝cos(πs/2)Γ(s)/ 2^s－1π^s・ζ(s)

が得られました。

＜2つの関数等式＞

オイラ－による関数等式（非対称型）

　ζ(1－s)=cos(sπ/2) Γ(s)ζ(s)／2^s－1π^s・・・・（1）

から、リ－マンによる関数等式（対称型）

　π^－s/2Γ(s/2)ζ(s)＝π^－(1－s)/2Γ((1－s)/2)ζ(1－s) ・・・・（2）

を導出します。

（2）式より

　ζ(1－s)＝π^－s/2Γ(s/2)ζ(s) π^(1－s)/2 /Γ((1－s)/2)

　　　　　＝π^－s+1/2Γ(s/2) /Γ((1－s)/2)・ζ(s)

より、

　　cos(sπ/2) Γ(s)／2^s－1π^s＝π^－s+1/2Γ(s/2) /Γ((1－s)/2)

すなわち

　　Γ((1－s)/2) Γ(s) cos(sπ/2)＝2^s－1π^1/2Γ(s/2)

が成り立つことを示します。

ガンマ関数の相反公式

　Γ(s)Γ(1－s)＝π/sin(πs)

でs→(1－s)/2に置き換えると、1－(1－s)/2＝(1＋s)/2より

　Γ((1－s)/2)Γ((1＋s)/2)＝π/sin(π(1－s)/2)

　Γ((1－s)/2)Γ((1＋s)/2)＝π/cos(πs/2)　　・・・（5）

が成り立ちます。

また、ルジャンドルの2倍公式

　Γ(2s)＝2^2s-1/π^1/2・Γ(s) Γ(s+1/2)

でs→s/2に置き換えると、

　Γ(s)＝2^s-1/π^1/2・Γ(s/2) Γ((s+1)/2) 　・・・（6）

が成り立ちます。

(5)、（6）式の辺々を掛け、Γ((s+1)/2)を消去すると

　Γ((1－s)/2)・Γ(s)＝π/cos(πs/2)・2^s－1/π^1/2・Γ(s/2)

すなわち

　Γ((1－s)/2) Γ(s) cos(sπ/2)＝2^s－1π^1/2Γ(s/2)

が成り立つことが示されました。関数等式はゼ－タ関数の定義域を拡大する場面でよく用いられす。

 

＜複素関数論からフーリエ変換を導く方法＞

　f(t)＝∫_{[－∞、∞]} F(ω) e^iωt dt

   F(ω)＝1/2π・∫_{[－∞、∞]} f(t) e^－iωt dt

 

＜コ－シ－の積分公式＞

F(z)が有限領域Dで正則であり、領域D内部の単一閉曲線Cz内の点zにおける値は、

　F(z)＝1/2πi・∫_Cz F(ξ)/(ξ－z) dξ

と表される。

 

F(z)をn回微分すると

　F⁽ⁿ⁾(z)＝n！／2πi・∫_Cz F(ξ)/(ξ－z) ⁿ⁺¹ dξ

となる。よってz＝0のとき

   F⁽ⁿ⁾(0)/ n！＝1/2πi・∫_C0 F(ξ)/ξⁿ⁺¹ dξ　・・・（1）

である。いま

   Σ_n＝Σ_{n＝－∞～∞}

と略記する。関数F(z)をｚ＝0の周りでローラン展開すると、F(z)は

　F(z)＝Σ_n F⁽ⁿ⁾(0)/ n！zⁿ

と表される。（1）式を代入すると

　F(z)＝Σ_n [1/2πi・∫_C0 F(ξ)/ξⁿ⁺¹ dξ] zⁿ・・・（2）

と書ける。

　e^{i2π(t＋T)/T}＝e^i2πt/T・e^i2π＝e^i2πt/T

であるから、関数f(t)を

　f(t)＝F( e^i2πt/T)　　・・・（3）

と定義すると、関数f(t)は

　f(t＋T)＝f(t)

により、周期Tの周期関数になる。（2）式を用いると

　f(t)＝Σ_n [1/2πi・∫_C0 F(ξ)/ξⁿ⁺¹ dξ] ( e^i2πt/T) ⁿ

　　＝Σ_n C _n ( e^i2πt/T) ⁿ

と書ける。いま、ξ＝e^i2πs/T によってξからsに変数変換する。

　dξ＝i2π/T・e^i2πs/T ds

s＝－T/2のとき、ξ＝e^{i2π(－T/2)/T}＝e^－iπ＝－1

s＝＋T/2のとき、ξ＝e^i2π(+T/2)/T＝e^+iπ＝－1

つまりξが半径1の円周C₀上を動くとき、sは－T/2からT/2に動くことに注意すると、

C _n＝1/2πi・∫_C0 F(ξ)/ξⁿ⁺¹ dξ

    ＝1/2πi・∫_{[－T/2、T/2]} F(e^i2πs/T)/ (e^i2πs/T)ⁿ⁺¹ 2πi /T・e^i2πs/T ds

　＝1/T∫_{[－T/2、T/2]} F(e^i2πs/T)/ (e^i2πs/T)ⁿ⁺¹・e^i2πs/T ds

　＝1/T∫_{[－T/2、T/2]} F(e^i2πs/T) (e^i2πs/T)^－n ds

　＝1/T∫_{[－T/2、T/2]} f(s)e^－i2πsn/T ds

となる。

　ω_n＝2πn/T

とおくと、

　Δω＝ω_n+1－ω_n＝2π/T → 0　as  T → ∞

　1/T＝Δω/2π

なので、

f(t)＝Σ_n C _n e^{iωn t}

　 ＝∫ _{[－∞、∞]} dω[∫_{[－T/2、T/2]} f(s)e^－iωs ds] e^iωt

    ＝∫ _{[－∞、∞]} dω[1/2π∫_{[－∞、∞]} f(s)e^－iωs ds] e^iωt

    ＝∫ _{[－∞、∞]} F(ω) e^iωt dω

F(ω)＝1/2π∫_{[－∞、∞]} f(s)e^－iωs ds

が示された。