＜ルジャンドルの2倍公式の証明＞

　Γ(2s)＝2^2s-1/π^1/2・Γ(s) Γ(s+1/2)

を証明する。

今、B(x,y)＝Γ(x)Γ(y)/Γ(x＋y) より

　B(x,1/2)＝Γ(x)Γ(1/2)/Γ(x+1/2)

　B(x,x)＝Γ(x)² /Γ(2x)

が成り立つ。先ほど証明された式

　B(x,1/2)＝2^2x－1B(x,x)

に代入すると、

　Γ(x)Γ(1/2)/Γ(x+1/2)＝2^2x－1Γ(x)² /Γ(2x)

を得る。Γ(1/2)＝π^1/2より

　Γ(2x)＝2^2x－1π^－1/2Γ(x)Γ(x+1/2)

が成り立つことが示された。

Γ(n)=(n-1)!　、Γ(1/2)=π^－1/2なので、ｘ＝4のとき

Γ(8)＝2^2*4－1π^－1/2Γ(4)Γ(4+1/2)＝2³Γ(4)・2⁴Γ(4+1/2)π^－1/2

2⁴Γ(4+1/2)π^－1/2＝2⁴・7/2 Γ(7/2)π^－1/2＝2⁴・7/2・5/2・3/2・1/2 Γ(1/2)π^－1/2

　　　　　　　＝7・5・3・1

2³Γ(4)＝2³（3・2・1）＝6・4・2

Γ(8)＝7！＝7・5・3・1・6・4・2

を表しています。

＜ガンマ関数の相反公式＞

　Γ(x)Γ(1－x)＝π/sin(πx)

を証明します。その前にこの公式の直感的な説明をします。

Γ(x)はｘ＝0，-1，-2，・・・でのみ1位の極をもちます。Γ(1-x)はｘ＝1，2，3，・・・でのみ1位の極をもちます。

f(x)=1/Γ(x)Γ(1－x)は全ての整数で1位の零点をもちます。ｘをｘ+1にすると

　Γ(ｘ+1)Γ(1-（ｘ+1））＝ｘΓ(ｘ)Γ(-ｘ）＝-ｘΓ(ｘ)Γ(1-ｘ）

ので、f(x+2)＝－f(x+1)＝f(x)　となり、f(x)は周期2の関数であることが分かります。ｘ＝1/2で最大値

　f(1/2)＝1/Γ(1/2)Γ(1－1/2)＝1/π

をとります。よってf(x)＝sin(πx)/πと予想できます。

証明に入ります。先ほどもとめたベータ関数の性質は

（4）：B(x,1－x)＝∫_[0，∞] u^x－1/(1＋u) du

（5）：B(x,1－x)＝Γ(x)Γ(1－x)

ですから、

　∫_[0，∞] x^a－1/(1＋x) dx＝π/sin(πa)　0＜a＜1

を示せばよいことが分かります。

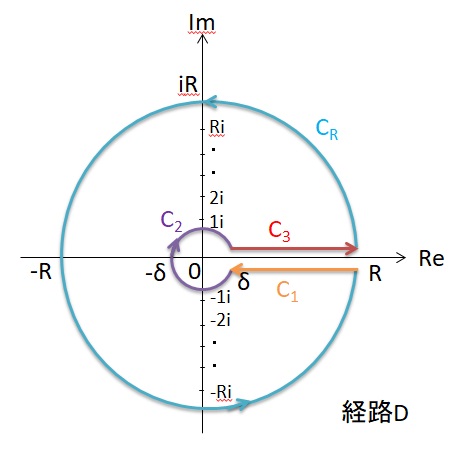
D積分閉路を使って

　f(z)＝z^a－1/(1＋z)

の複素積分を行います。D積分閉路は

　D＝C₁＋C₂(ε)＋C₃＋C_R

からなります。

 

 

 

 

 

ε→0、R→∞で

　∫_C2(ε)f(z)dz→0、∫_CR f(z)dz→0

となります。0＜a＜1より、－1＜a－1＜0、に注意すると

　－ε+1≦εe^iθ+1≦ε+1より、1/｜(εe^iθ＋1)｜≦1/(1－ε)

なので、z＝εe^iθ、dz＝iεe^iθdθ、0＜a＜1、より

　｜∫_C2(ε)f(z)dz｜≦∫_[0、2π]｜(εe^iθ) ^a－1｜/｜εe^iθ＋1｜｜iεe^iθ｜dθ

　　　　　　　≦εε^a－1/(1－ε) 2π＝2πε^a/(1－ε)　→　0　as　ε→0

同様に、－1＜a－1＜0、より

　｜∫_CRf(z)dz｜≦∫_[0、2π]｜(Re^iθ) ^a－1｜/｜Re^iθ＋1｜｜iRe^iθ｜dθ

　　　　　　　≦2πR・R^a－1/R＝2πR^a－1→　0　as　R→∞

となります。

z ^a－1はz＝0で特異点を持ちますが、z＝0は経路D内には含まれません。

D積分閉路内の極は、z＝－1だけです。f(z)のz＝－1での留数は

　Res[f,－1]＝lim_[x→－1] (z＋1) z ^a－1/(z＋1)＝(e^iπ) ^a－1＝e^iπa e^－iπ＝－e^iπa

　∫_D f(z)dz＝2πi Res[f,－1]＝2πi (－e^iπa)

となります。

C₃上での偏角は0だからz＝xe⁰代入して、ε→0、R→∞で

　∫_C3 f(z)dz＝∫_[ε、R] x^a－1/(1＋x) dx　→　I＝∫_[0、∞] x^a－1/(1＋x) dx

C₁上での偏角は2πなので、z＝xe^2πi代入して、ε→0、R→∞で

　z^a－1＝(xe^2πi) ^a－1＝x ^a－1e^2πiae^－2πi＝x ^a－1e^2πia

　∫_C1 f(z)dz＝∫_[R、ε] e^2πia x^a－1/(1＋x) dx　→∫_[0、∞] x^a－1/(1＋x) dx

となります。従って

　2πi (－e^iπa)＝I＋0＋I＋0＝(1－e^2πia)I

これをIについて解くと

　I＝2πi (－e^iπa)/ (1－e^2πia)＝2πi (－e^iπa)／(－e^iπa) (e^iπa－e^－iπa)

　　＝π/sin(πa)

が得られます。

 

ゼ－タ関数とガンマ関数とベータ関数は相互に密接な関係があります。ここではベータ関数のいくつかの性質を紹介します。これらはルジャンドルの倍公式やガンマ関数の相反公式を証明するのに役立ちます。

＜ベ－タ関数の諸性質＞

ベ－タ関数は

　B(x,y)＝∫_[0，1] t^x－1(1－t)^y－1dt  (x>0,y>0)

で定義されます。

（1）B(x,y)＝B(y,x)

　t’＝1－tとおくと、

B(x,y)＝－∫_[1，0] (1－t’)^x－1 t’^y－1dt’ ＝B(y,x)

（2）B(x,y)＝2∫_[0，π/2] sin^2x－1θcos^2y－1θdθ

　　t＝sin²θとおくと、dt＝2sinθcosθdθ

　　B(x,y)＝∫_[0，π/2] (sin²θ)^x－1(cos²θ)^y－12sinθcosθdθ

　　　　＝2∫_[0，π/2] sin^2x－1θcos^2y－1θdθ

（3）B(x,y)＝Γ(x)Γ(y) /Γ(x＋y)

　　t＝s²とおくと、dt＝2sdsより

　　Γ(x)＝∫_[0，∞] t^x－1 e^－t dt＝2∫_[0，∞] s^2x－1 e^－ss ds

　　Γ(x)Γ(y)＝4∫_[0，∞] t^2x－1 e^－tt dt・∫_[0，∞] s^2y－1 e^－ss ds

　　t＝rcosθ、s＝rsinθとおくと、t²＋s²＝r²、dtds＝rdrdθ

　　4∫_[0，π/2]dθ∫_[0，∞] dr (rcosθ)^2x－1 (rsinθ)^2y－1 e^－rr

　＝2∫_[0，π/2]dθ∫_[0，∞] dr cos^2x－1θsin^2y－1θ・2∫_[0，∞] r^2(x＋y)－2e^－rr rdr

　t＝r²とおくと、dt＝2rdrより、r^2(x＋y)－2＝t^(x＋y)/r²＝t^(x＋y)－1

　　Γ(x)Γ(y)＝B(x,y)・∫_[0，∞] t^(x＋y)－1e^－t dt＝B(x,y)・Γ(x＋y)

が示された。

（4）B(x,y)＝∫_[0，∞] u^x－1/(1＋u)^x＋y du

　　B(x,y)＝∫_[0，1] t^x－1(1－t)^y－1dt 

　において、t＝u/(1＋u)とおくと　

　　1－t＝1－u/(1＋u)＝1/(1＋u)

　(1＋u)t＝u、u－ut＝t、u＝t/(1－t)　→u＝0～∞
　du＝[(1－t)+t]/(1－t)² dt＝1/(1－t)² dt＝(1＋u) ² dt

　→　dt＝du/(1＋u) ²

であるから

　t^x－1(1－t)^y－1dt＝[u/(1＋u)]^x－1(1＋u)^－y＋1(1＋u)^－2du
＝u^x－1(1＋u)^－(x＋y) du

　B(x,y)＝∫_[0，∞] u^x－1(1＋u)^－(x＋y) du

が示された。

y＝1－xのとき

　B(x,1－x)＝∫_[0，∞] u^x－1(1＋u)^－(x＋y) du

　　　　　＝∫_[0，∞] u^x－1/(1＋u) du

が成り立つ。

（5）B(x,1－x)＝Γ(x)Γ(1－x)

　B(x,y)＝Γ(x)Γ(y)/Γ(x＋y) において

　　y＝1－xと置くと、Γ(x＋y)＝Γ(1)＝1より

　B(x,1－x)＝Γ(x)Γ(1－x)/Γ(1)＝Γ(x)Γ(1－x)

（6）B(x,1/2)＝2^2x－1B(x,x)

　B(x,1/2)＝B(1/2 ,x)＝∫_[0，1] t^－1/2 (1－t) ^x－1dt

　t＝u²とおくと、t^－1/2＝u^－1、dt＝2udu

　B(x,1/2)＝2∫_[0，1] (1－u²)^x－1 du

　　　　＝∫_[0，1] (1－u²)^x－1 du－∫_[0，－1] (1－u²)^x－1 d(－u)

　　　　＝∫_[0，1] (1－u²)^x－1 du＋∫_[－1，0] (1－u²)^x－1 du

　　　　＝∫_[－1，1] (1－u²)^x－1 du

　s＝(1+u)/2とおくと、u＝2s－1、s＝0～1

　　1－u＝1－2s+1＝2(1－s)

　　1－u²＝(1－u) (1＋u)＝4(1－s)s

　B(x,1/2)＝2∫_[0，1] (4(1－s)s)^x－1 2ds

　　　　＝2^2x－1∫_[0，1] (1－s) ^x－1s^x－1 ds

　　　　＝2^2x－1B(x,x)

が示された。