[12]素数定理の証明手順のまとめ

[０]関数の定義　P；素数の集合

・リーマンのゼ－タ－関数：ζ(s)＝Σ_{[n＝1～∞]} 1/n^s、Re(s)＞1

　（nに関する無限級数）

・ファイ関数：Φ(s)＝Σ_[p∊P] log(p)／p^s、Re(s)＞1

　（すべての素数に関する和をとる）

・チェビシェフのシータ関数：θ(x)＝Σ_[p≦x] log(p)

  （X以下の素数pに関する和をとる）

・素数の個数関数：π(x)＝Σ_[p≦x]1

[Ⅰ]命題1　Re(s)＞1、ζ(s)＝Π_[p∊P] [1／(1－1/p^s)]　オイラ－積表示の存在

（1）Re(s)＞1でζ(s)のディリクレ級数表示は収束する。

（2）ζ(s)のディリクレ級数表示はオイラ－積表示に一致する。

（3）Re(s)＞1でζ(s)のオイラ－積表示は収束する。

（4）ζ(s)は、s＞0（s≠1）に拡張することができる。

[Ⅱ] 命題2　ζ(s)－1/(ｓ－1)はRe(s)＞0で正則である。

（1）∫_[1,∞]1/x^s dx＝1/(s‐1)　for　s＞1

（2）s∫_[n,x] 1/t^s+1 dt＝1/n^s－1/x^s

（3）｜t^s+1｜＝t^Re(s)+1

（4）ζ(s)－1/(ｓ－1)≦｜s｜ζ( Re(s)+1) for　s＞1　

[Ⅲ] 命題3　Φ(s)－1/(ｓ－1)はRe(s)≧1で正則である。

（1）ζ’(s)/ζ(s) ＋1/(s－1)　はRe(s)≧1で正則である。

（2）Φ(s)‐1/(s‐1)＝‐[ζ′(s)／ζ(s)＋1/(s‐1)]－Σ[p] log(p)／p^s(p^s‐1) 　を示す。

（3）右辺2項目Σ[p] log(p)／p^s(p^s‐1)はRe(s)＞1/2で正則である。

（4）Re(s)＝1でζ(s)＝0なる零点が存在しない。

[Ⅳ] 命題4　θ(x)＝Ｏ(x)　i.e.　∃ｋ＞0　｜θ(x)｜≦ｋx

（1）2nlog2≧θ(2n)－θ(n)

（2）2^ｍ+1・log2＞θ(2^m)

  (3) θ(x) ≦4log2・x

[Ⅴ] 命題5　∫_[1，∞] [θ(x)－x]／x² dxは収束する。

・[Ⅲ] 、[Ⅳ]、[定理A]を用いて証明する。

（1）Φ(s)＝s∫_[1，∞] θ(x)／x^ｓ+1dx、Re(s)＞1

（2）f(t)＝θ(e^t)e^－t－1　（t≧0）は有界、g(z)＝∫_[0，∞] f(t)exp[－zt] dtが存在する

（3）g(z)＝Φ(z+1)／(z+1)－1/z　　Re(z)＞0

（4）g(z)はRe(z)≧0で正則

（5）g(0)＝∫_[0，∞] f(t) dt＝∫_[1，∞] [θ(x)－x]／x² dx　が収束する。

[Ⅵ] 命題6　θ(x)～x　i.e.　lim_[x→∞] θ(x)/x＝1

・任意のε＞0、∃x＞0　1－ε＜θ(x)/x＜1＋εを示す。

・背理法を用いて矛盾を示す。任意の正数ｘに対して、∃ε＞0

（1）1＋ε≦θ(x)/x　は矛盾を生じるので、θ(x)/x＜1＋ε　by [Ⅴ]

（2）θ(x)/x≦1－ε　は矛盾を生じるので、1－ε＜θ(x)/x 　by [Ⅴ]

[Ⅶ] 素数定理　Lim _[x→∞] π(x) logx／x＝1

（1）1←θ(x)/x≦π(x)log(x)/x　by [Ⅵ]

（2）π(x)log(x)/x≦1/(1－ε)・θ(x)/x＋log(x)/x^ε→1/(1－ε)　→1

[定理A]　Newmanの解析定理

t≧0で有界かつ可積分な関数f(t)に対して、

g(z)＝∫_[0，∞] f(t)exp[－zt] dt　Re(z)＞0

がRe(z)≧0で正則であれば、

　g(0)＝∫_[0，∞] f(t) dt

が存在する。つまり正則関数

　g_T(z)＝∫_[0，T] f(t)exp[－zt] dt

に対して、

　lim_[T→∞]g_T(0)＝g(0)

が存在する。

[定理A]　Newmanの解析定理の証明手順

（1）g(0)－g_T(0)＝1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz

（2）A＝｜g(0)－g_T(0)｜＝｜1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz｜

　　　≦A₊＋A_－≦A₊＋A_－1＋A_－2 → 2B/R（T→∞）→ 0 （R→∞）

（3）A₊≦B/R、Re(z)＞0　

（4）A_－1＝｜1/2πi・∫_C－g_T(z)e^zT(1＋z²/R²)／z dz｜≦B/R　

（5）A_－2＝｜1/2πi・∫_C－g(z)e^zT(1＋z²/R²)／z dz｜→ 0

[Ⅷ]　Newmanの解析定理の証明

（1）g(0)－g_T(0)＝1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz を示します。

コ－シ－の積分公式より、領域Dで正則な複素関数f(z)のD内の閉曲線C上の積分に関して、

閉曲線Cで囲まれた領域の点αにおいて

• f(α)＝1/2πi・∫_C f(z)／(z－α) dz

が成り立つ。閉曲線Cの半径R＞0として、

• f(z)＝[g(z)－g_T(z)]e^zT(1＋z²/R²)

を考えると、f(z)は以下で定義される領域Dで正則であることが分かります。

任意の閉曲線C上のg_T(z)の積分は、∫_C e^－ztdz＝0より

• ∫_C g_T(z)dz＝∫_C (∫_[0,T]f(t)e^－ztdt)dz＝∫_[0,T] f(t) (∫_C e^－ztdz)dt＝0

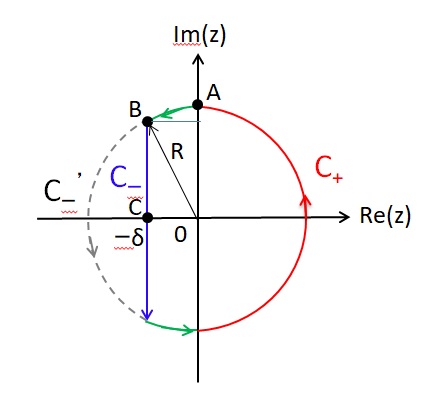
です。モレラの定理から、g_T(z)は任意の閉曲線C内で正則です。解析定理の前提より、g(z)はRe(z)≧0で正則なので、Re(z)＝0上の任意の点z＝it（－∞≦t≦∞）でテ－ラ－展開でき、その収束円内のzでも正則です。従って、十分大きなR＞0と十分小さなδ＞0において、「｜z｜≦R　かつ－δ≦Re(z)」となる領域Dの境界線を閉曲線Cとすると、閉曲線Cの内部領域Dでg(z)とg_T(z)は正則です。e^zT(1＋z²/R²)も正則なので、f(z)は正則関数となり、

コ－シ－の積分公式を適用できます。いまz＝0で

• f(0)＝g(0)－g_T(0)

です。α＝0として、コ－シ－の積分公式を適用すると

• f(0)＝g(0)－g_T(0)＝1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz

が成り立ちます。

（2）A＝｜g(0)－g_T(0)｜＝｜1/2πi・∫_C [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz｜

　　　≦A₊＋A_－≦A₊＋A_－1＋A_－2 → 2B/R（T→∞）→ 0 （R→∞）

を示します。そのために、積分路を

• C＝C₊ (Re(z)＞0)＋C_－(Re(z)＜0)

に分け、

　A₊＝｜1/2πi・∫_C+ [g(z)－g_T(z)]e^zT(1＋z²/R²)／z dz｜

　A_－＝｜1/2πi・∫_C－[g(z)－g_T(z)] e^zT(1＋z²/R²)／z dz｜≦ A_－1＋A_－2

とします。ここで

　A_－1＝｜1/2πi・∫_C－’g_T(z)e^zT(1＋z²/R²)／z dz｜

　A_－2＝｜1/2πi・∫_C－g(z)e^zT(1＋z²/R²)／z dz｜

とします。これから

　A≦A₊＋A_－≦A₊＋A_－1＋A_－2 → 2B/R（T→∞）→ 0 （R→∞）

を示します。

 

 

 

 

 

 

 

（3）A₊≦B/R、Re(z)＞0　を示します。

z＝Re^iθとおいて積分変数をzからθに変換すると、dz＝i Re^iθdθ

　　A₊≦1/2π｜∫_C＋｜g(z)－g_T(z)｜e^Re(z)T [1＋z²/R²]／z dz｜

非積分関数

[1＋z²/R²]／z＝[1＋R²e^2iθ/R²]/Re^iθ＝2[R(e^iθ＋e^－iθ)/2]/R²＝2Re(z) /R²

より

　　A₊≦1/2π∫_C＋｜g(z)－g_T(z)｜e^Re(z)T2Re(z) /R²｜dz｜

いま、｜f(t)｜≦B（有界）なので

｜g(z)－g_T(z)｜＝｜∫_[T，∞] f(t)exp[－zt] dt｜≦B｜∫_[T，∞] exp[－Re(z)t] dt｜

　　　　　　＝－B/ Re(z)[ exp[－Re(z)t]]_t＝T,∞＝B/ Re(z)・e^－Re(z)T

です。従って、

A₊≦1/2π∫_C＋B/ Re(z)・e^－Re(z)T・e^Re(z)T2Re(z) /R²｜dz｜＝(B/πR²) ∫_C＋｜dz｜

となります。∫_C＋｜dz｜＝πRより

　　A₊≦B/R

が得られます。

（4）A_－1＝｜1/2πi・∫_C－g_T(z)e^zT(1＋z²/R²)／z dz｜≦B/R　を示します。

Re(z)＜0より、C- ’の積分経路を用いる。｜Re(z)｜＝－Re(z)に注意して

　｜g_T(z)｜＝｜∫_[0，T] f(t)e^－zt dt｜≦B∫_[0，T] e^－Re(z)t dt＝B/(－Re(z))[e^－Re(z)t]t=0,T

　　　　　＝B/(－Re(z))[e^－Re(z)T－1]≦B/(－Re(z))e^－Re(z)T

　A_－1＝｜1/2πi・∫_C－’g_T(z)e^zT(1＋z²/R²)／z dz｜

　　　≦1/2π・∫_C－’｜g_T(z)｜e^Re(z)T｜(1＋z²/R²)／z｜｜dz｜

　　　≦1/2π・[B/(－Re(z))e^－Re(z)T] e^Re(z)T[2Re(z) /R²]・∫_C－’｜dz｜

　　　　＝1/2π・B/(－Re(z)) [2｜Re(z)｜/R²]・πR＝B/R

（5）A_－2＝｜1/2πi・∫_C－g(z)e^zT(1＋z²/R²)／z dz｜→ 0 as T→∞　を示す。

有界閉集合C－上のTを含まない複素関数の絶対値には最大値があり、

　｜g(z) (1＋z²/R²)/z｜≦M

なる正数Mが存在します。

　　A_－2≦M/2π・｜∫_C－e^zT dz｜≦M/2π・∫_C－e^Re(z)T｜dz｜

となる。C－上の積分路を弧AB上と直線BC上の2つに分けて、実行します。

1）弧AB上：z＝R e^iθ　(π/2≦θ≦λ)、cos(λ)＝－δ/R　｜dz｜＝Rdθ

2）直線BC上：z＝－δ＋it　(0≦t≦√(R²－δ²))　 ｜dz｜＝dt

実軸に対する対称性から、積分経路をIm(z)≧0に限定して、積分値を2倍します。

A_－2≦2・M/2π・[∫_AB e^Re(z)T｜dz｜＋∫_BC e^Re(z)T｜dz｜]

　　＝M/π・[∫_{[(π/2≦θ≦λ]} e^Rcos(θ)T Rdθ －∫_{[0≦t≦√(R2－δ2)]} e^－δT dt ]

t=cos(θ)とおくと、dt＝－sin(θ)dθ＝－√(1－t²) dθより、t：0→cos(λ)＝－δ/R

　＝M/π・[－∫_{[(0≦t≦－δ/R]} e^RTt R／√(1－t²) dt －√(R²－δ²)・e^－δT ]

　≦M/π・[－∫_{[(0≦t≦－δ/R]} e^RTt R／√(1－(δ/R)²) dt －√(R²－δ²)・e^－δT ]

　　＝M/π・[－R²／√(R²－δ²)・∫_{[(0≦t≦－δ/R]} e^RTt dt －√(R²－δ²)・e^－δT ]

ここで

　∫_{[(0≦t≦－δ/R]} e^RTt dt＝1/RT・[e^RTt]_{t＝0, －δ/R}＝1/RT・[e^－Tδ－1]

ですから、δ＞0より、

A_－2≦M/π・[R²／√(R²－δ²)・1/RT・[1－e^－Tδ]－√(R²－δ²)・e^－δT ] → 0 as T→∞

が得られます。

（3）～（5）より、

　　｜g(0)－g_T(0)｜＝A≦A₊＋A_－≦2B/R → 0  as  T→∞, R→∞

が成り立ちます。よって

　lim_[T→∞]g_T(0)＝g(0)

が存在することが証明されました。

 

＜コ－シ－の積分公式＞

領域Dで正則な複素関数f(z)のD内の閉曲線C上の積分に関して、Cで囲まれた領域の点z＝αにおいて

• f(α)＝1/2πi・∫_C f(z)／(z－α) dz

が成り立つ。Cの向きは反時計回りを正とする。

証明）z＝αの近傍で、正則関数f(z)を

• f(z)＝f(α＋z－α)＝f(α)＋f’(α) (z－α)＋1/2・f’’(α) (z－α)²＋・・・

と展開すると、正則関数1，z、z²、z³、・・は閉曲線C内に極をもたないので、コーシ－の積分定理よりC上の積分でゼロになります。

∫_C f(z)／(z－α) dz＝∫_C[f(α)＋f’(α) (z－α)＋1/2・f’’(α) (z－α)²＋・]／(z－α) dz

　＝f(α)・∫_C 1/(z－α) dz ＋f’(α)∫_C dz＋1/2・f’’(α) ∫_C (z－α) dz＋・・・

　＝f(α)・∫_C 1/(z－α) dz

となります。z＝α+e^iθとおくとdz＝ie^iθdθ、θ＝0～2πより

　∫_C 1/(z－α) dz＝∫_{[0≦θ≦2π]}i e^iθ/e^iθdθ＝2πi

従って

　∫_C f(z)／(z－α) dz＝2πi f(α)

となります。

 

＜モレラの定理＞～コ－シ－の積分定理の逆

閉曲線C上の連続関数f(z)の積分に関して、∫_C f(z)dz＝0　ならば、f(z)は閉曲線C内で正則である。

証明）z₀からzまでの積分経路をCとします。

　F(z)＝∫_C＝[z_0,z_] f(z)dz

zからz＋Δzまでの経路Lを、

• ξ(t)＝z＋Δz・t　(0≦t≦1)

で定義します。

• dz＝ξ’(t)dt＝Δzdt

が成り立ち、

　F(z＋Δz)＝∫_C+L f(z)dz

と書けます。以下にF(z)の導関数F’(z)が存在し、F’(z)＝f(z)となることを示します。

　　｜[F(z＋Δz)－F(z)]/ Δz－f(z)｜＝｜[∫_C+L f(z)dz－∫_C f(z)dz] /Δz－f(z)｜

　＝｜(1/Δz)∫_[z,z＋Δz] f(z)dz－f(z)｜＝｜(1/Δz)∫_[0,1] f(ξ(t)) Δzdt－f(z)｜

　＝｜∫_[0,1] f(ξ(t)) dt－f(z)｜

　≦∫_[0,1]｜f(ξ(t))－f(z)｜dt ≦∫_[0,1]εdt＝ε

ここでf(ξ)は連続なので、任意のε＞0に対して、｜f(ξ)－f(z)｜＜ε を満たす、｜ξ－z｜＜ΔzなるΔz＞0が存在します。ε→0とΔz→0は対応しています。

　Iim_[Δz→0]｜[F(z＋Δz)－F(z)]/ Δz－f(z)｜≦Iim_[Δz→0]ε(Δz)→0

よって、F(z)の導関数F’(z)が存在し、F’(z)＝f(z)となります。F(z)の導関数が存在するから、F(z)は正則です。グルサの定理より、F’(z)も正則になります。F’(z)＝f(z)なので、f(z)も正則になります。従って、閉曲線Cに対して、∫_C f(z)dz＝0　ならば、f(z)はC内で正則であることが示されました。

 

[Ⅶ] 素数定理　Lim _[x→∞] π(x) logx／x＝1　の証明

（1）Lim_[x→∞]π(x)log(x)/x≧1　を示します。

チェビシェフのシータ関数には

• θ(x)＝Σ_[p≦x] log(p)≦{Σ_[p≦x]1} log(x)＝π(x) logx

なる性質があります。x＞0について、[Ⅵ]より

• π(x) logx／x ≧ θ(x)／x　→1　as　x→∞

よって、Lim_[x→∞]π(x)log(x)/x≧1　となります。

（2）Lim_[x→∞] π(x) log(x)/x≦1　を示します。

任意のε＞0に対して、十分大きいxをとれば、ε・log(x)を大きくとることができるから、

　log(x)－ε・log(x)≦log(p)≦log(x)　→　0＜x^1－ε≦p≦x　

なる素数pが存在します。

θ(x)＝Σ_[p≦x] log(p) ≧ Σ[x^1－ε＜p≦x] log(p) ≧Σ[x^1－ε＜p≦x] log(x^1－ε)

　 ＝(1－ε)log(x)・Σ[x^1－ε＜p≦x]1＝(1－ε)log(x)・(π(x)－π(x^1－ε))

よって、

   θ(x) ≧(1－ε)log(x)・(π(x)－π(x^1－ε))

   θ(x)／x (1－ε) ≧π(x) log(x)/x－π(x^1－ε) log(x)/x

すなわち

  π(x) log(x)/x ≦ 1/(1－ε)・θ(x)/x＋π(x^1－ε) log(x)/x

                     ≦1/(1－ε)・θ(x)/x＋x^1－ε・log(x)/x

となる。ここで

    x^1－ε・log(x)/x＝log(x)/x^ε＝1/ε・log(x^ε)/x^ε

より、任意のε＞0に対して

  π(x) log(x)/x≦1/(1－ε)・θ(x)/x＋1/ε・log(x^ε)/x^ε　→　1/(1－ε)　as x→∞

が成り立つ。極限をとると

    Lim_[x→∞] π(x) log(x)/x≦1

となる。

（3）（1）と（2）から、素数定理

　　Lim_[x→∞] π(x) log(x)/x＝1

が証明されました。

 

[定理A]　Newmanの解析定理

t≧0で有界かつ可積分な関数f(t)に対して、

g(z)＝∫_[0，∞] f(t)exp[－zt] dt　Re(z)＞0

がRe(z)≧0で正則であれば、

　g(0)＝∫_[0，∞] f(t) dt

が存在する。つまり正則関数

　g_T(z)＝∫_[0，T] f(t)exp[－zt] dt

に対して、

lim_[T→∞]g_T(0)＝g(0)

が存在する。

[Ⅵ] θ(x)～x　の証明

　θ(x)～x の定義は、lim_[x→∞] θ(x)/x＝1　です。これは、任意のε＞0、∃x＞0に対して、

　　1－ε＜θ(x)/x＜1＋εと同値です。あるいは

• 任意のλ＞1に対してθ(x)＜λx　かつ
• 任意のλ＜1に対してλx＜θ(x)

と同値です。この命題を否定して、

• λ＞1に対してθ(x)≧λx　かつ
• λ＜1に対してλx≧θ(x)

なるλが存在するとして、矛盾を導きます。

（1）λ＞1に対してθ(x)≧λx　なるλが存在するとして、矛盾を導きます。

　λ＞1のとき、x≦t≦λxなるtに対して、θ(t)≧θ(x)であり

• θ(t)≧θ(x)≧λx　→　(θ(t)－t)／t²≧(λx－t)／t²

　であるから、

• ∫_[x,λx] [(θ(t)－t)／t²] dt ≧∫_[x,λx] [(λx－t)／t²] dt＝∫_[1,λ] [(λ－s)／s²] ds＝δ(λ)＞0

　が成り立ちます。ここでt=xsとおいて、積分変数をtからsに変換しました。

(Ⅴ)より積分

• F(x)＝∫_[1,x] [(θ(t)－t)／t²] dt　→　F（∞）as　x→∞

は収束するので、x→∞で

• 0＜δ(λ)≦∫_[x,λx] [(θ(t)－t)／t²] dt＝F(λx)－F(x)　→　0　as　x→∞

となり、矛盾することが示せました。

（2）λ＜1に対してλx≧θ(x)なるλが存在するとして、矛盾を導きます。

　λ＜1のとき、λx≦t≦xなるtに対して、θ(t)≦θ(x)であり、

• θ(t)≦θ(x)≦λx　→　(θ(t)－t)／t²≦(λx－t)／t²

　であるから、

• ∫_{[λx, x]} [(θ(t)－t)／t²] dt ≦∫_{[λx, x]} [(λx－t)／t²] dt＝∫_[λ,1] [(λ－s)／s²] ds＝δ(λ)＜0

　が成り立ちます。ここでt=xsとおいて、積分変数をtからsに変換しました。

　(Ⅴ)より積分

• F(x)＝∫_[1,x] [(θ(t)－t)／t²] dt　→　F（∞）as　x→∞

　は収束するので、x→∞で

• 0＞δ(λ)≧∫_{[λx, x]} [(θ(t)－t)／t²] dt＝F(x)－F(λx)　→　0　as　x→∞

　となり、矛盾します。よって背理法より、lim_[x→∞] θ(x)/x＝1　が示されました。

[Ⅴ]　∫_[1，∞] [θ(x)－x]／x² dxは収束する。

上記の積分の収束を命題[Ⅲ] 、[Ⅳ]、[定理A]を用いて5段階で証明します。

（1）　Φ(s)＝s∫_[1，∞] θ(x)／x^ｓ+1 dx、Re(s)＞1　が成り立つことを示します。

s∫_[1，∞] θ(x)／x^ｓ+1 dx＝s∫_[1，∞]Σ_[p≦x] log(p)／x^ｓ+1 dx

＝s∫_[1，2]0 dx＋s∫_[2，3] log2／x^ｓ+1dx＋s∫_[3，5](log2＋log3)／x^ｓ+1 dx＋・・・

＝－[log2／x^ｓ]_x=2,3－[(log2+log3)／x^ｓ]_x=3,5－[(log2+log3+log5)／x^ｓ]_x=5,7＋・・・

＝－(log2／3^s－log2／2^s)－[ (log2+log3)／5^s－(log2+log3)／3^s) ]

　－[ (log2+log3+log5)／7^s－(log2+log3+log5)／5^s) ]

　－[ (log2+log3+log5+log7)／11^s－(log2+log3+log5+log7)／7^s) ]－・・・

＝log2／2^s＋log3／3^s＋log5／5^s＋log7／7^s＋・・・

＝Σ_[p]logp／p^s ＝Φ(s)

（2）f(t)＝θ(e^t)e^－t－1　（t≧0）は有界かつ可積分である、ことを示します。

 (Ⅲ)でx＝e^tとして、あるＫ＞0が存在して、｜θ(e^t)｜≦Ｋe^t だから

   ｜f(t)｜＝｜θ(e^t)e^－t－1｜≦｜θ(e^t)｜e^－t＋1＝Ｋe^t e^－t＋1＝Ｋ＋1　

となり、f(t)は有界な関数である。

（3）g(z)＝Φ(z+1)／(z+1)－1/z　　Re(z)＞0　を示します。

x＝e^tとおいて置換積分を実施する。dx＝xdt、t：0→∞、x：1→∞、

e^－zt＝(e^t)^－z＝x^－zに注意すると、

　g(z)＝∫_[0，∞] (θ(e^t)e^－t－1)exp[－zt] dt

　　＝∫_[1，∞] (θ(x)x^－1) x^－z dx/x－[e^－zt／－z]_t=0,∞

　　＝∫_[1，∞] (θ(x)／x^z＋2)dx－1/z

　　＝Φ(z＋1)／(z＋1)－1/z

が示されました。

（4）g(z)はRe(z)≧0で正則である、ことを示します。

(Ⅲ)より、Φ(s)－1/(ｓ－1)はRe(s)≧1で正則なので、s＝z＋1として

　　Re(s)＝Re(z)＋1≧1　→　Re(z)≧0　

Φ(z＋1)－1/zはRe(z)≧0で正則なので、正則関数h(x)を用いて、

　　Φ(z＋1)－1/z＝h(x)　

と表せます。

　g(z)＝Φ(z＋1)／(z＋1)－1/z

　　　＝（h(x)＋1/z）／(z＋1)－1/z＝

　　　＝h(x)／(z＋1)＋1／z(z＋1)－1/z

　　　＝h(x)／(z＋1)＋[1－(z＋1)]／z(z＋1)

　　　＝[h(x)－1]／(z＋1)

　g(z)は、z=－1に極をもちますが、Re(z)≧0で正則であることが示されました。

（5）g(0)＝∫_[0，∞] f(t) dt＝∫_[1，∞] [θ(x)－x]／x² dx　が収束する、ことを示します。

　（2）より関数f(t)＝θ(e^t)e^－t－1はt≧0で有界かつ可積分であり、

　（4）よりg(z)＝∫_[0，∞] f(t)exp[－zt] dt がRe(z)≧0で正則である

従ってNewmanの解析定理により

　　g(0)＝∫_[0，∞] f(t) dt＝∫_[0，∞] (θ(e^t)e^－t－1) dt

が存在します。（3）と同様にx＝e^tとおいて置換積分を実施すると、

　　g(0)＝∫_[1，∞] (θ(x)x^－1－1) dx/x＝∫_[1，∞] [θ(x)－x]／x² dx

が収束することが示されました。

[Ⅳ] θ(x)＝Ｏ(x)　の証明

チェビシェフのシータ関数：θ(x)＝Σ_[p≦x] log(p) がオーダ－xであること、すなわち

・　∃ｋ＞0　｜θ(x)｜≦ｋx          

を3段階で証明します。

（1）2nlog2≧θ(2n)－θ(n)　の証明

2項定理より

2²ⁿ＝(1＋1)²ⁿ＝Σ_{[k＝1～2n] 2n}C_ｋ1^k1^2n-k≧_2nC_n＝2n・(2n－1)・(2n－2)・・(n+2)・(n+1)／n！

_2nC_nは自然数なので、分母のｎ！は約分されて1になります。しかしn+1＜p≦2nの素数pはn！の中には存在しないので、約分されずに分子に残ります。右辺はn+1＜p≦2nの素数pの積Π_{[n+1≦p≦2n]} pより大きくなるので、

・　2²ⁿ≧Π_{[n+1≦p≦2n]} p

が成り立ちます。一方

・　θ(2n)－θ(n)＝Σ_[p≦2n] log(p)－Σ_[p≦n] log(p)＝Σ_{[n+1≦p≦2n]} log(p)

なので、

・　exp[θ(2n)－θ(n)]＝exp[Σ_{[n+1≦p≦2n]} log(p)]＝Π_{[n+1≦p≦2n]} p

です。よって

・　2²ⁿ≧exp[θ(2n)－θ(n)]　→　2n・log2≧θ(2n)－θ(n)

が成り立ちます。

Eg.  ₁₆C₈=16・15・14・13・12・11・10・9／8・7・6・5・4・3・2・1

　　　　＝2・3・13・11 ＞11・13（8+1≦11,13≦16）

（2）2^ｍ+1・log2＞θ(2^m)　の証明

　上式にn＝2^k－1を代入すると、2^k・log2≧θ(2^k)－θ(2^k－1)が成り立つ。

k＝1：　2¹・log2≧θ(2¹)－θ(1)　

k＝2：　2²・log2≧θ(2²)－θ(2¹)

k＝3：　2³・log2≧θ(2³)－θ(2²)

・・・ 　　・・・・

k＝m－1：2^m－1・log2≧θ(2^m－1)－θ(2^m－2)

k＝m：　 2^m・log2≧θ(2^m)－θ(2^m－1)

をすべて加えると、θ(1)＝0より

　　log2・Σ_[k＝1～m]2^k ≧θ(2^m)

を得ます。ここで

　　Σ_[k＝1～m]2^k＝2^m+1－2＜2^m+1

だから、

　　2^m+1 log2＞θ(2^m)

が示されました。

(3) θ(x) ≦4log2・x

x≧1なる整数xに対して、∃m∊N、2^m≦x≦2^m+1

θ(x)は非減少関数なので、（2）より

　　0≦θ(x) ≦θ(2^m+1)＜2^m+2 log2≦4 log2・2^m≦4 log2・x

よって、K＝4 log2とおくと

　　θ(x) ≦Kx、　→　θ(x)＝O(x)

が示されました。