＜テータ関数の変換公式＞

ｓ＞0のとき

　θ(s)＝Σ_{n＝－∞～∞}exp(－πsn²)

に対して、

　θ(1/s)＝√s・θ(s)

が成り立つ。

[証明]　関数f(t)を

　f(t)＝exp(－πst²)

とおくと、

　θ(n)＝Σ_{n＝－∞～∞}f(n)

である。f(t)のフーリエ変換をF(m)とすると

　F(m)＝∫_{[－∞、∞]} exp(－πst²)e^－i2πmt dt

である。これをｍで一回微分すると

　d F(m)/dm＝∫_{[－∞、∞]} exp(－πst²) (－i2πt)e^－i2πmt dt

　　　　　  ＝i/s・∫_{[－∞、∞]} (－2πst)exp(－πst²) e^－i2πmt dt

                    ＝i/s・∫_{[－∞、∞]} (d/dt)exp(－πst²) e^－i2πmt dt

                  ＝i/s・[exp(－πst²) e^－i2πmt]t=_－∞、∞－i/s∫_{[－∞、∞]} exp(－πst²) (－i2πm) e^－i2πmt dt

　　　　   ＝－2πm/s・∫_{[－∞、∞]} exp(－πst²) e^－i2πmt dt

　　　　   ＝－2πm/s・F(m)

となる。微分方程式を解くと

　[logF(m)]’＝F’(m)/ F(m)＝－2πm/s
    logF(m)＝－πm²/s

を解いて、
   F(m)＝F(0)exp(－πm²/s)

が得られる。

　F(0)＝∫_{[－∞、∞]} exp(－πst²) dt

ここで、u＝√(πs)・t　と置くと

　F(0)＝1/√(πs)∫_{[－∞、∞]} exp(－u²) du

　　　＝1/√(πs)・√π　＝1/√s

従って、フ－リエ変換後の関数は

　　F(m)＝1/√s ・exp(－πm²/s)

となる。ここで

f(t)＝exp(－πst²)　は[－∞、∞]区間上の連続関数であるから、Poissonの和公式より

　Σ_n f(n)＝Σ_n F(n)

すなわち

　Σ_n exp(－πsn²)＝Σ_n 1/√s ・exp(－πn²/s)

が成り立つ。いま、θ(s)＝Σ_{n＝－∞～∞}exp(－πsn²)　より

　θ(s)＝1/√s ・θ(1/s)

が成り立つことが示された。

 

[補題]　正の実数xに対して、

　Σ_n exp[－π(n＋α)²/x]＝√x Σ_n exp[－πn²x＋ i2πnα]

が成り立つ。

・α＝0を代入すると、θ(1/x)＝√x ・θ(x)　が成り立つ。

[証明]　

  f_αx(y)＝exp[－π(y＋α)²/x]

とおいて、

  Σ_n f_αx(y)＝√x Σ_n exp[－πn²x＋ i2πnα]

を示す。Poissonの和公式より

　Σ_n f_αx(n)＝Σ_n∫_{[－∞、∞]} f_αx(y) e^－i2πny dy

＝Σ_n ∫_{[－∞、∞]} exp[－π(y＋α)²/x] e^－i2πny dy

ここで、y+α＝xuとおくと、

  Σ_n f_αx(n)＝Σ_n∫_{[－∞、∞]} exp[－πxu²] e^{－i2πn(xu－α)} dy

                 ＝Σ_n e^i2πnα∫_{[－∞、∞]} exp[－πxu²] e^－i2πnxu xdu

ここで

    －πxu²－i2πnxu＝－πx(u²＋i2nu)＝－πx(u＋in) ²－πxn ²

であるから、

     Σ_nf_αx(n)＝xΣ_ne^i2πnαexp[－πxn ²]∫_{[－∞、∞]} exp[－πx(u＋in)²] du　　

　　　　　  ＝xΣ_ne^i2πnαexp[－πxn ²]・lim_N→∞ I(N)

ここで
    I(N)＝∫_[－N、N] exp[－πx(u＋in)²] du＝∫_Aexp[－πx(u＋in)²] du　　

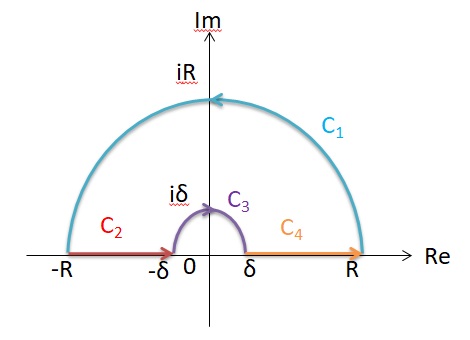
とした。この積分の経路は複素平面で、

  A：z＝u＋in（－N≦u≦N）

である。コーシ－の定理より、非積分関数は正則関数なので、経路A上の複素積分を以下のB→C→Dに変えることができる。

   I(N)＝∫_B→C→D exp[－πx(z)²] dz　　

において

　B：z＝－N+it、0≦t≦n

　C：z＝t、－N≦t≦N

　D：z＝N+it、0≦t≦n

経路Bでの積分は

　I_B(N)＝∫_[n、0] exp[－πx(－N＋it)²] dt　　

          ＝－exp[－πxN²]∫_[0、n] exp[(1－it/N)²] dt　

ここでt’＝t/N　とおくと、

  I_B(N)＝∫_[0、n] exp[(1－it/N)²] dt

       ＝1/N・∫_[0、n/N] exp[(1－it’)²] dt’　→ 0　as　N→∞

となり、N→∞での積分値はゼロになる。

同様に経路Dでの積分は

   I_D(N)＝∫_[0、N] exp[－πx(N＋it)²] dt

          ＝1/N・∫_[0、n/N] exp[(1＋it’)²] dt’　→ 0　as　N→∞

となり、N→∞での積分値はゼロになる。経路Cでの積分は

   I_C(N)＝∫_[－N、N] exp[－πxt²] dt　　

　　　＝1/√(πx) ・∫_[－N、N] exp[－t²] dt　→　√π/√(πx)＝1/√x　as　N→∞

となり、N→∞での積分値は1/√xとなる。

従って

　lim_N→∞ I(N)＝lim_N→∞｛I_B(N)＋I_C(N)＋I_D(N)｝＝1/√x　

を得る。結局

  Σ_n f_αx(n)＝x Σ_ne^i2πnαexp[－πxn ²]・lim_N→∞ I(N)

　　　　＝x Σ_ne^i2πnαexp[－πxn ²] 1/√x
              ＝√x・Σ_nexp[－πxn ²＋i2πnα]

が成り立つことが示された。

＜Poissonの和公式＞

[－∞、∞]区間上の任意の連続関数f(x)とそれをフーリエ変換した関数

　F(n)＝∫_{[－∞、∞]} f(t)e^－i2πnt dt

に対して、

　Σ_{n＝－∞～∞} f(n)＝Σ_{n＝－∞～∞} F(n)

が成り立つ。

[証明]　 連続関数f(t)に対して

　g(t)＝Σ_{n＝－∞～∞}f(n+t)

を定義する。

　g(0)＝Σ_{n＝－∞～∞}f(n)

であり、g(t)は

　g(t+1)＝g(t)

なる周期性を持つので、フ－リエ級数展開

　g(t)＝Σ_{n＝－∞～∞}c_n e^i2πnt

ができる。t=0のとき

　g(0)＝Σ_{n＝－∞～∞}c_n

が成り立つ。一方、

　F(m)＝Σ_{n＝－∞～∞}∫_[n、n+1] f(t)e^－i2πmt dt

　　　＝Σ_{n＝－∞～∞}∫_[0、1] f(t+n)e^{－i2πm(t+n)} dt

　　　＝∫_[0、1] [Σ_{n＝－∞～∞}f(t+n)] e^－i2πmt dt

　　　＝∫_[0、1] g(t) e^－i2πmt dt

　　　＝∫_[0、1] [Σ_{n＝－∞～∞}c_n e^i2πnt] e^－i2πmt dt

　　　＝Σ_{n＝－∞～∞}c_n・[∫_[0、1] e^i2π(n－m)t dt]

　　　＝Σ_{n＝－∞～∞}c_n・δ_nm

　　　＝c_m

従って

　g(0)＝Σ_{n＝－∞～∞}f(n)＝Σ_{n＝－∞～∞} F(m)

が成り立つ。

 

ディリクレ積分

　∫_[0,∞] sin(x) /x dx＝π/2　

を複素積分

　∫_C e^iz /z dz＝0

で求めます。

閉積分経路Cを

　C＝C₁＋C₂＋C₃＋C₄

に分けます。ここで

　C₁：z＝Re^iθ0≦θ≦π

　C₂：z＝x　–R≦x≦－δ

　C₃：z＝δe^iθ0≦θ≦π

　C₄：z＝x　δ≦x≦R

とします。閉積分経路C内にz=0の極は含まれないので、Cでの積分はコーシ－の定理よりゼロになります。

（1）C₁の積分

　0≦sinθ≦1　かつ　2θ/π≦sinθ（0≦θ≦π）、

ですから、

　｜exp(iRe^iθ)｜＝｜exp{iR(cosθ+ i sinθ)}｜

　　　　　　　＝｜exp{iRcosθ}・exp{－R sinθ)}]｜

　　　　　　　＝e^{－R sinθ}

　　　　　　　≦e^－R2θ/π

従って

　｜∫_C1 e^iz /z dz｜＝｜∫_[0，π]  exp(iRe^iθ) /Re^iθ ・iRe^iθdθ｜

　　　　　　　　 ≦∫_[0，π] e^－R2θ/πdθ

　　　　　　　　 ＝－π/2R・[e^－R2θ/π] _θ＝0，π

＝π/2R・(1－e^－2R)　→　0　as　R→∞

C₁の積分はRが無限大になるとゼロになります。

（2）C₂の積分

ここで　x’＝‐xに置き換えると

　∫_C2 e^iz /z dz＝∫_[R，δ] e^‐ix’ /x’ dx’＝－∫_[δ、R] e^‐ix’ /x’ dx’

となります。

（3）C₃の積分

　　∫_C3 e^iz /z dz＝∫_[π，0]  exp(iδe^iθ) /δe^iθ ・iδe^iθdθ

　＝i∫_[π，0]  {1+(iδe^iθ)+O(δ²)｝dθ

　→　i∫_[π，0] dθ＝－iπ　as　δ→0

（4）C₄の積分

　∫_C3 e^iz /z dz＝∫_[δ、R] e^ix /x dx

となります。以上より

0＝∫_C1 e^iz /z dz＋∫_C2 e^iz /z dz＋∫_C3 e^iz /z dz＋∫_C4 e^iz /z dz

　　＝∫_CRe^iz /z dz－∫_[δ、R] e‐^ix /x dx＋∫_[δ、R] e^ix /x dx－iπ

　　＝∫_CRe^iz /z dz ＋∫_[δ、R](e^ix－e^‐ix) /x dx－iπ

　　＝∫_CRe^iz /z dz ＋2i∫_[δ、R]sin(x) /x dx－iπ

ここで　δ→0かつR→∞　とすると

　2i∫_[0、∞]sin(x) /x dx－iπ＝0

すなわち

　∫_[0、∞]sin(x) /x dx＝π/2

が得られます。複素積分を用いると簡単にディリクレ積分の値が求められました。