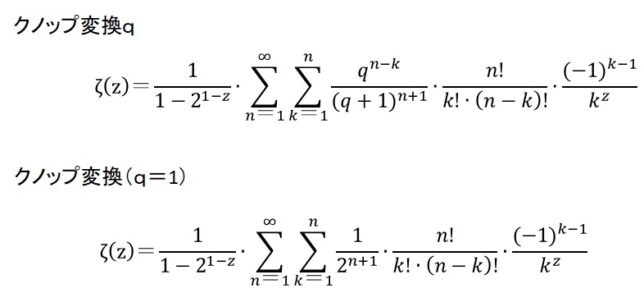ゼ－タ関数は

　ζ(z)＝∑_k=1～∞1/k^z＝1＋1/2^z＋1/3^z＋1/4^z＋・・・　　　Re(z)＞1

という複素関数です。ゼ－タ関数の零点とは、ζ(z)＝0となるｚのことです。今回はゼ－タ関数の零点を計算してみました。前回、ゼ－タ関数は

　ζ(z)＝∏_p(1/[1－1/p^z])＝1／[1－1/2^z]・[1－1/3^z]・[1－1/5^z]・[1－1/7^z]・・・

のように素数の積で表示できることを示しました。このことが示唆するように、ゼ－タ関数の零点と素数には密接な関係があることが知られています。

前回、イ－タ関数η(z)　（前回はη(z)をL(z)と書きました。）

　η(z)＝∑_k=1～∞(－1)^k－1/k^z＝1－1/2^z＋1/3^z－1/4^z＋1/5^z－1/7^z＋・・・          Re(z)＞0

を使うと、ゼ－タ関数

　ζ(z)＝η(z)/(1－2^1－z)　　Re(z)＞0　ｚ≠1

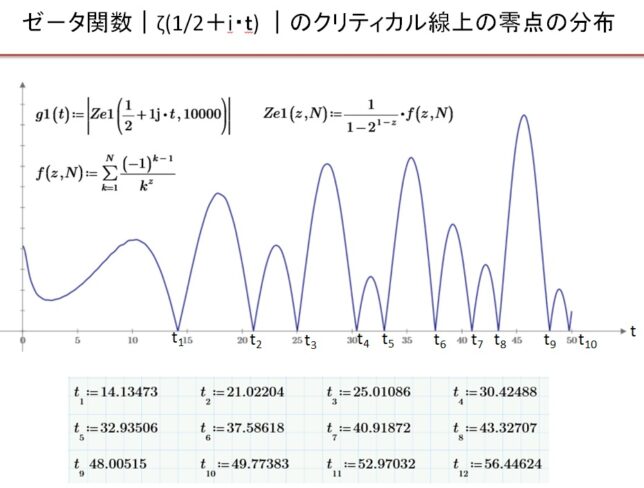
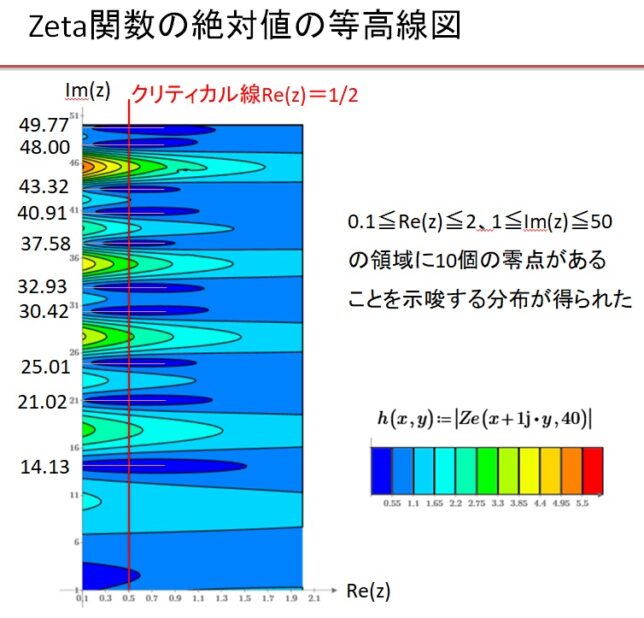
の定義域は、Re(z)＞0に拡大できることを示しました。ゼ－タ関数は、ガンマ関数を用いて表示することでRe(z)＜0にも拡大できます。ゼ－タ関数の零点には、ｚ＝－2、－4、－6・・・・に自明な零点があることが分かっています。1859年にリ－マンはゼ－タ関数の非自明な零点はRe(z)＝1/2の線上に分布すると予想しました。今回は

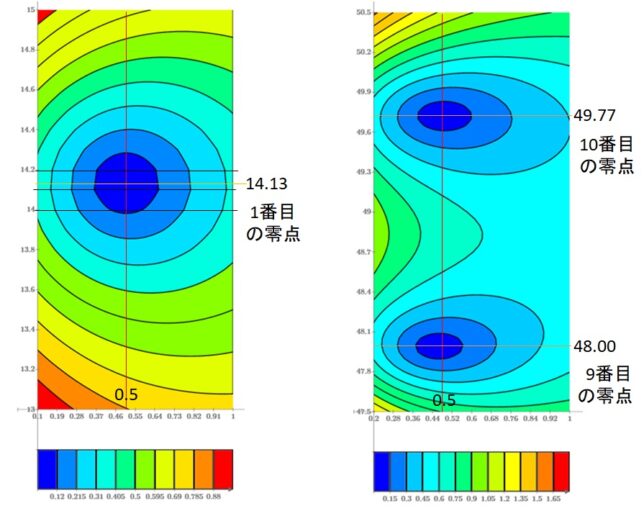
　ζ(z)＝η(z)/(1－2^1－z)＝0

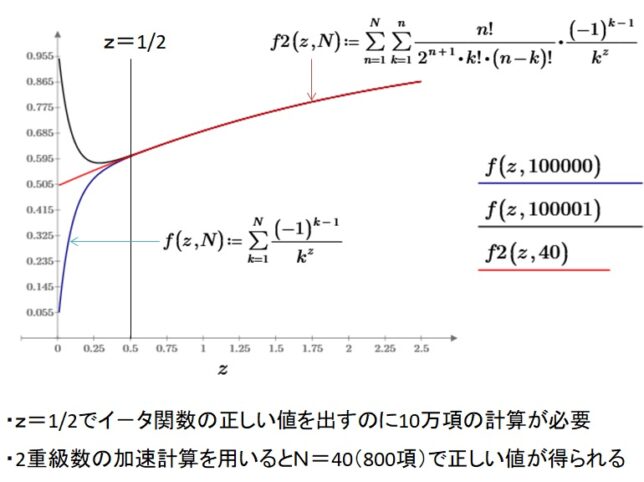
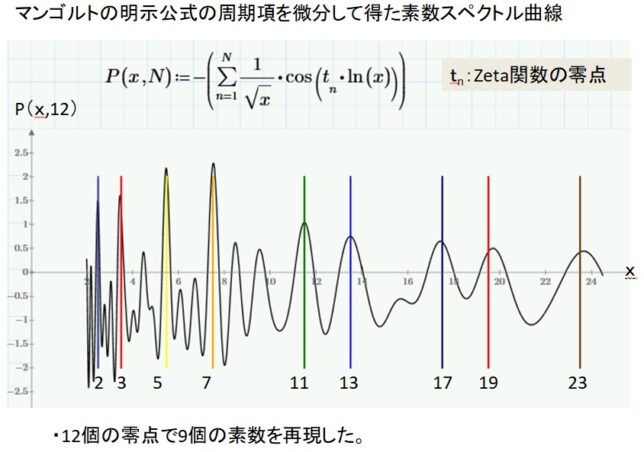
を満たす非自明な零点の分布を調べて見ました。問題は、無限和を有限和で置き換えると、級数の収束が遅いので、誤差が大きくなってしまうことです。私のパソコンでは、10万項の級数を計算しても、Re(z)＝1/2の線上の零点の虚数座標を有効数字4桁の精度（t₁＝14.13）でしか求められませんでした。そこでクノップ変換を行い級数の収束性を高めました。　N＝40（40×40/2＝800項）の計算で零点を有効数字7桁の精度（t₁＝14.13473）で求めることができました。マンゴルトの明示公式の周期項を微分して得た素数スペクトル曲線に12個の零点を入れて9個の素数を再現しました。

クノップ変換では。収束が遅い級数に「1に収束する級数」を挿入して和の順番を変えることで、級数の収束性を高めます。パラメータｑの値を変えることで、収束速度と収束領域が変わります。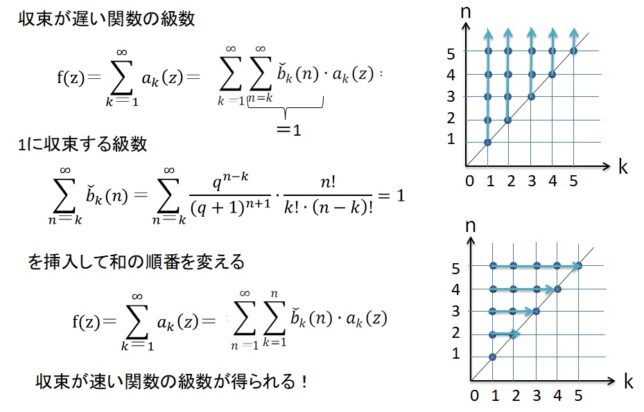

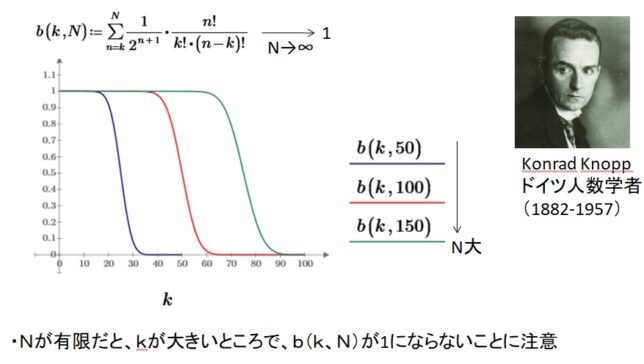
関数b(k,N)はNが無限大になると1になりますが、Nが有限だと、ｋがN/2より大きい所では1より小さくなります。　コンラッド・クノップ(1882～1957)は無限級数の収束を研究したドイツ人の数学者です。