









IPCC第4次評価報告書によれば、放射強制力は、対流圏での循環バランスが取れた状態を初期状態とし、これに何らかの原因によってずれが生じたとき、成層圏の気温の変化を考慮したうえで、再び対流圏での循環バランスが取れるようになるまでに変わる放射の量として定義されています。CO2濃度変化が大きいほど放射強制力Fは増大します。
放射強制力は、フロンのような微量ガスの濃度増加に対しては線形に変化します。CO2ガスに対しては濃度増加比の対数に比例して変化すると考えられています。IPCC (1990)およびMyhre (1998)らは、
の式を持ちいています。例えば、地球大気中の二酸化炭素の平均濃度が300ppmから400ppmに上昇した場合CO2の放射強制力ΔFは
となります。産業革命時のCO2濃度285ppmを基準にすると、2100年直前にCO2濃度が2倍になると予測されています。この場合、CO2の放射強制力は
となります。このとき
つまり地表気温の上昇は約3Kと推定されています。
IPCC(気候変動に関する政府間パネル)委員会はCO2濃度変化の異なる4つのシナリオを検討しました。それらはRCP2.6、RCP4.5、RCP6.0、RCP8.5と呼ばれています。これは2100年におけるCO2の放射強制力Fが、
の4つの場合に相当しています。
有効射出温度
現在の気候では、観測可能な大気上端での上向き長波放射(OLR=Outgoing Longwave Radiation)の観測値は235W/m2(Kiehl and Trenberth 1997)です。地球を黒体とみなした時の有効射出温度は、ステファンボルツマンの法則
・R(=235)=σT4=5.67×10-8T4
より、T=254K(=-19℃)です。これは、エネルギ平衡モデル
から求めた温度、
T=255K(=-18℃)とほぼ一致しています。これは温室効果ガスがないときの地表面の温度に相当します。気温減率6.5[K/km]なので、-18℃の高度は、地表面温度15℃のとき、
です。大気上端8kmでの温度は-37℃ですが、地球からの熱放射は-18℃の大気からの黒体放射と考えられます。
1℃あたりの大気上端での放射束の変化は
となります。これをプランク応答と呼びます。我々の体温を36℃とすると、517[W/m2] の熱放射と6.7[W/m2 K]のプランク応答があります。体温が1℃上がると、6.7[W/m2]の熱が逃げるので、体が冷えます。つまりプランク応答には負のフィ-ドバック効果があります。
水蒸気の応答はプランク応答の70%程度
だと言われています。よって気候感度ΔTは
となります。2100年にCO2の増加により放射強制が3.7[W/m2]となるシナリオでは、数十年かけて3[K]程度の気温上昇があると予測されます。
大気上端での熱エネルギの収支を考えることで、温暖化のメカニズムを理解できます。
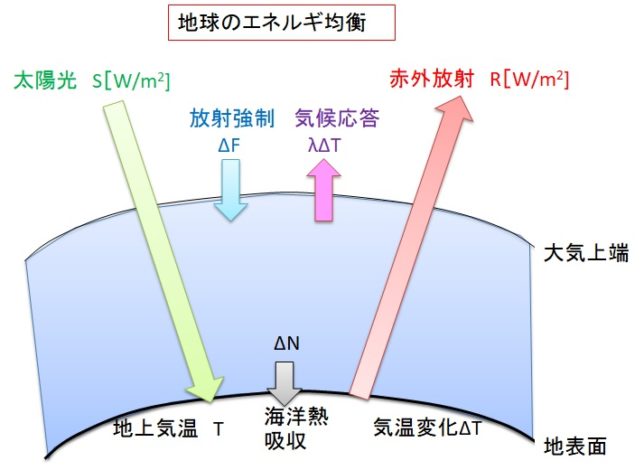
太陽光の照射密度S[W/m2]と赤外線の放射密度R[W/m2]の差をN[W/m2]とします。Nはいわば大気に蓄えられるエネルギ密度です。
ここでTは大気上端の温度、PCO2はCO2圧力、PH2Oは水蒸気圧力、Albedoは太陽光の反射率、Cloudは雲量を表し、いずれも温度Tに依存します。赤外放射Rはこれらの諸元の関数になっています。ここで太陽放射Sは1365W/m2で一定であると仮定します。十分時間が経つと、S=Rとなり、大気に蓄えられた出力密度Nはゼロの平衡状態(厳密には定常状態)になります。仮にCO2濃度が急に2倍になると、地表からの赤外放射がCO2によって遮られるので、大気上端での赤外放射Rは小さくなります。このとき
となり、大気にエネルギが蓄えられ、気温が上がり、大気上端の温度Tも上昇します。しかし時間が経つと、大気のエネルギNは海洋に拡散していき、やがてN=0となります。このとき大気上端の温度はΔTだけ上昇した状態でS=Rになると考えられます。
バランス方程式
まず簡単のため、Albedo、Cloudは一定とします。Sは定数なので、CO2濃度がΔPCO2変化すると、温度がΔT変化するので、大気に
ΔN=-(∂R/∂PCO2)ΔPCO2-(∂R/∂T)ΔT-(∂R/∂PH2O)(∂PH2O /∂T)ΔT
のエネルギが蓄積します。ここで
と定義します。FはCO2の放射強制力(Radiation Forcing)と呼ばれています。λpはプランク応答、λH2Oは水蒸気応答と呼ばれています。ここで応答パラメタλ(フィードバックパラメタ)を
と定義すると、よく知られたバランス方程式
が得られます。FはCO2濃度上昇による大気を加熱する効果、λΔTは大気を冷却する効果を表しています。λpは冷却すなわち負の応答効果、λH2Oは加熱すなわち正の応答効果を表しています。但し1/λを気候感度パラメ-タと呼ぶ場合もあるので注意が必要です。
一般に応答パラメタλは
雲による影響は、計算が難しいですが、太陽光の反射による冷却効果より惑星放射の吸収よる加熱効果の方が高いので正のフィ-ドバック効果があると考えられています。しかしながら応答パラメタλの値は、おおまかにはプランク応答と水蒸気応答の値で決まります。水蒸気の濃度が高いと、応答パラメタλが小さくなるので、気候感度ΔTは増大します。
温度上昇の時間変化
時刻t=0で、ΔT=0すなわち、ΔN=Fです。t=∞で、ΔN=0となります。その時間変化の時定数をτとすると、大気に蓄積するエネルギは
と書けます。バランス方程式に代入すると
これをΔTについて解くと、
が得られます。これは、十分時間が経ち、バランスを回復した後の温度上昇ΔTがF/λとなることを示しています。ΔTを平衡気候感度あるいは気候感度と呼ばれています。
ちなみに現在の放射平衡の下では、応答パラメタλは
程度とされています。
気象学者たちは、今後100年間に平均気温が2℃~3℃程度上昇する可能性が高いと警告しています。夏は熱くなるけど、冬は温暖になるから、それほど深刻な問題ではない、と思う人もいるかもしれません。しかしこの程度の温暖化で、災害や病害を引き起こす極端気象の発生件数は倍増してしまうことは深刻な問題です。計算機シミュレ-ションの結果は、温暖化によって、暑い地域はより暑く、寒い地域はより寒くなること、多雨地域はより雨量が増加し、乾燥地域はより乾燥するという傾向を示しています。温暖化でその地域がどのような被害を受けるかが予測できるようになります。
累積炭素排出に対する過渡気候応答TCRE(=Transient Climate Response to Cumulative Carbon Emissions)
2013年のIPCC委員会の報告によると、明治維新があった1870年頃からの平均気温の増加は、1870年から累積されたCO2排出量によって決まっています。これを累積炭素排出に対する過渡気候応答(TCRE)と言います。現在はこれまで400ギガトン炭素のCO2を排出し、当時から1℃気温が上昇しています。今後さらに400ギガトン炭素のCO2を累積排出すれば、当初から気温が2℃上昇すると予測されています。つまりこれは毎年のCO2の排出量を減らしても、CO2を排出する限り、いつかは2℃の気温上昇を引き起こしてしまうことを意味しています。温暖化は我々の子孫の生活を困難にする可能性が高いと考えられます。おそらく化石燃料を消費する生活から循環的な生活に変えていかなければならないのでしょう。
計算機シミュレ-ションだけでは温暖化現象のメカニズムは理解できません。それとは別に、マクロな視点で温暖化のメカニズムを理解する必要があります。
地表には太陽光が降り注ぎ、15℃程度に温められた地表は大量の赤外線を宇宙に向けて放出します。CO2などの温室効果物質はこの赤外線を吸収し、宇宙と地表に放出します。それによって、地表は15℃を維持しています。CO2がなければ、地表は-18℃程度になると考えられています。
世界気象機関(WMO=World Meteorological Organization)は、2019年1月に世界各地は異常気象に見舞われたと発表しました。米国のミネソタ州では-53.8度の猛烈な寒さ、オーストラリアのアデレードでは最高気温46.6度を記録しました。WMOのターラス事務局長は一連の異常気象と地球温暖化の関連を指摘しています。2018年の夏、甲府では1か月も猛暑日が続きました。新聞では34年ぶりのことだと報道されました。WMOは30 年間に1 回以下の頻度で発生する気象現象を異常気象あるいは極端気象と定義しています。
一方、観測デ-タによると、地球全体の年平均気温は増加傾向を示しています。年平均気温は1900年から1940年まで0.4℃上昇し、1940年から1980年まで0.1℃低下しましたが、1980年から2000年にかけて0.5℃上昇しています。産業革命前のCO2濃度は285ppmでしたが、ハワイのマウナロア山で観測されるCO2濃度は指数関数的に増大しており、2013年には400ppmを超えました。2100年になる前にCO2濃度は570ppm(=285ppm×2)になると予測されています。
気象学者たちは
・現在起きている異常気象に対する温暖化の寄与はどのくらいか?
・それが近未来にどう変わるか?
・人間の活動がどの程度温暖化に寄与しているのか?
といったことを調査しています。
全気候モデルGCM(=Global Climate Model)
気象学者たちは、全気候モデル(GCM)などの地球システムの計算機シミュレ-ションを用いて、社会経済学者との協力のもと将来の温室効果ガスの排出量を仮定した上で、温暖化の程度を予測しています。具体的には、温室効果ガスの濃度とそれらの放射強制から、気温や降水量などの気候応答を計算し、その結果を用いて温室効果ガスの濃度を計算し直しています。計算機の進歩により、現在では地球を20km区画(メッシュ)、台風などは2kmメッシュで解像できるようになりました。シミュレ-ションで過去の平均気温の変動を再現する研究も進展しています。例えば2013年のIPCCの報告を見ると、CO2の濃度増加とエアロゾルによる冷却効果を取り入れることで、1960年から2000年までの0.8℃の温度上昇を再現することに成功しています。CO2の濃度増加がない場合には、観測された0.8℃の温度上昇は生じませんでした。まだ予測値の変動幅が大きいという問題はありますが、気象予測に計算機シミュレ-ションが有効であることは認められています。
文科省の統合的気候モデル高度化プログラムでは、過去60年間の日本の上空1500mでの気温(14℃~19℃)と、猛暑日の地点数をGCMモデルで計算し、それらの相関関係を調べています(今田)。その結果、平均気温が上がれば、熱波地点数が飛躍的に増加することが分かりました。2012年から2017年までの平均気温と熱波地点数のデ-タは、温暖化ありの条件で計算した結果の分布に一致しています。毎年の気候デ-タのばらつきは大きいですが、統計的に温暖化により異常気象が増えていることは言えそうです。
具体的には2℃の増加で3000以上の地点で毎年のように猛暑が起こる可能性が指摘されています。1℃の増加で日本上空の水蒸気量は7%増加します。水蒸気は、CO2より強い温室効果があるので、温暖化を加速させます。2018年夏の日本の猛暑はかなり極端でした。平均気温は2℃上昇し、猛暑日地点数は6500点を記録しました。ジェット気流の蛇行やオホ-ツク海高気圧などが、梅雨前線を停滞させて、7月には広島に大変な豪雨をもたらしました。しかしながら異常気象のメカニズムはまだ明確ではありません。
ラウドンの「光の量子論」(1994年)に量子力学的な散乱係数の詳細が書かれています。時間に依存した摂動論において、電気双極子相互作用の2次の寄与から散乱光子の放出速度τを計算します。単位時間に散乱によって光子ビ-ムから失われるエネルギ-ℏω/τと、単位断面積を単位時間に通過するエネルギcℏωn/Vとの比で散乱断面積を定義すると、
放出速度τを散乱断面積σに書き換えられます。1/τには∫dΩが含まれているので、微分断面積が求められます。これがクラマ-ス・ハイゼンベルグの公式です。原子が基底状態に戻る弾性散乱の場合は、
となります。εとεsは入射光子と散乱光子の単位偏光ベクトル、Dは電気双極子相互作用です。ω=ωiで発散しますが、厳密な扱いではωは虚部を有するので発散しません。
ω>ωiとω<ωiの場合を扱う場合には、上式で十分です。

1)トンプソン散乱の場合(ω>ωi)
光子の周波数ωが原子の励起周波数ωiより大きい場合には、絶対値の中の和は-ωi/ω2と近似できるので、
原子に束縛されている電子数をZとすると、総和則から
となるそうなので、微分断面積は
・ dσ/dΩ=[Z・re・(ε・εs)]2
となります。ここでreは古典的電子半径
です。つまり静電エネルギe2/4πεoreが静止エネルギmc2に等しくなる半径です。
このような高周波入射光の弾性散乱はトンプソン散乱として知られています。トンプソン散乱では散乱断面積は、原子構造と無関係に、電子数Zの2乗に比例します。
2)レ-リ-散乱の場合(ω<ωi)
光子の周波数ωが原子のどの励起周波数ωiより小さい場合には、分母のωを無視して
・dσ/dΩ=(eω/c)4/(4πεo ℏ)2∣∑i (1/ωi)・{(εs・D×ε・D)+(ε・D×εs・D) }∣2
となります。水素原子の場合はあらわに計算ができて、
となります。ここでℏωRは水素の基底状態のエネルギ
です。結局、水素原子に関するレ-リ-散乱の公式
が得られます。
なので、レ-リ-散乱の散乱断面積は波長の4乗に反比例することが量子論でも確かめられました。
3)共鳴散乱の場合(ω=ωi)
減衰係数γiを取り入れた表式は、i番目の準位への散乱断面積は
となります。励起状態はi=2だけだとして、散乱光子の全方向について積分すると、
となります。ここで減衰係数γは
です。よって散乱断面積は
の形に書き表せます。ω=ωoのとき、散乱断面積は入射光の波長λの2乗
となります。原子の第一励起状態との共鳴断面積は、波長だけで決まります。
電磁気学にはMKSA単位系(SI単位系)とCGS単位系(ガウス系)があります。
一世代前にはCGS単位系が使われていましたが、今ではMKSA単位系が用いられています。少し古い本を読むとCGS単位系が使われているので、CGS単位系とMKSA単位系の関係について知っておくと便利です。以下CGS単位系の物理量にはプライムをつけて区別します。
<CGS単位系とMKSA単位系の違い>
MKSA単位系では、ク-ロン力Fは
・ F=(1/4πε0)・Q1Q2/r2
ですが、CGS単位系では
・ F= Q’1Q’2/r2
とシンプルになります。
MKSA単位系では、電束密度と電界の関係は
・ D=ε0E+P
ですが、CGS単位系では
・ D’=E’+4πP’
となります。CGS単位系はよさそうに見えるのです。
しかしマクスウエル方程式に関してはMKSA単位系の方がすっきりしています。MKSA単位系では、マクスウエル方程式は
・ divD=ρ、divB=0、rotH=i+∂D/∂t、rotE=-∂B/∂t
ですが、CGS単位系では
・ divD’=4πρ’、divB’=0、rotH’=(4π/c)i’+(1/c)∂D’/∂t、
rotE’=-(1/c)∂B’/∂t
となります。CGS単位系はマクスウエル方程式に4πが出てきて目障りなのです。

<CGS単位系とMKSA単位系の関係>
電場の場合、次の3つの関係
・ Q= root(4πε0)Q’
・ D= root(ε0/4π)D’
・ E=E’/ root(4πε0)
を使えば換算できます。分極P=rQなので、P=root(4πε0)P’の関係です。
・ DS=Q(MKS系) →root(ε0/4π)D’=root(4πε0)Q’ →D’S=4πQ’(CGS系)
・ F=QE(MKS系) →F=root(4πε0)Q’ E’/ root(4πε0) →F=Q’ E’(CGS系)
・ D=ε0E+P(MKS系) → root(ε0/4π)D’=ε0E’/ root(4πε0)+root(4πε0)P’
・ → D’=E’+4πP’(CGS系)
が得られます。分極率αは
・ P=αε0E(MKS系) → root(4πε0)P’=αε0E’/ root(4πε0)
→ P’=(α/4π)E’(CGS系)
と変換されます。
計測可能な屈折率nを用いて、分極率を表します。単位体積当たりの分子数をNoとすると、分極率αが古典的に
・ α=(3/No)[(n2-1)/(n2+2)]
と表せることを説明します。
屈折率nの媒質では光速は
・ c=c0/n
と小さくなります。よって
・ n2=(c0/c)2=εμ/ε0μ0 ≒ ε/ε0
となります。
外部電場Eo内に設置された誘電体の内部の分子を含む半径roの球を考えます。分子に分極を引き起こす分子にかかる電場Eは
・ E=Eo+Ep+Ei
の3つの成分に分けて考えることができます。ここでEpは半径roの球をくり抜いた外側の誘電体の分極が球の中心につくる電場とします。Eiは球形の分極した誘電体が球の中心につくる電場とします。なお誘電体は等方的で、印加したEoと同じ方向に分極が生じるものとします。分子の位置を原点とし、外部電場の向きをx方向とし、x軸からの角度をθとします。
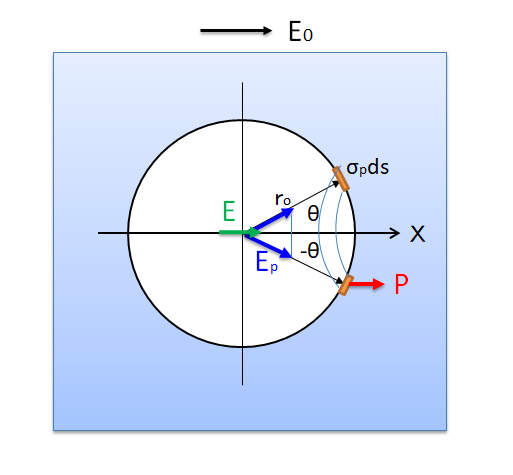
1)Epについて
外側の誘電体の分極により、半径roの球のx>0の内壁に負の面電荷、x<0の内壁に正の面電荷が生じています。角度をθの位置にある微小面積dsの電荷密度σpは
・ σp=∣P∣cosθ
となります。Pは単位体積当たりの双極子モーメントであり、P[Cm/m3]=P[C/m2]より面電荷と同じ次元をもっています。σpdsの電荷が原点につくる電場のx軸方向は
・ dE=∣P∣cosθds/4πεoro2 ・cosθ
角度θとθ+dθに挟まれた内壁の帯状の面積は、幅rodθをもつ半径ro・sinθの円ですから、ds=2πro・sinθrodθとなります。内壁の面電荷が原点につくる電場Epは
・ ∣Ep∣=∫[0、Π] ∣P∣cos2θ/[4πεo・ro2]・2πro2・sinθdθ
・ =∣P∣/2εo∫[-1、1] t2dt=∣P∣/2εo・2/3=∣P∣/3εo
・ Ep=+P/3εo
となります。
2)Eiについて
原点に微小距離d離れた正負の電荷qがあったとします。その点のポテンシャルφを考えると、双極子のエネルギは
・ U=qφ(d、0、0)-qφ(0、0、0)≒qd=p(dφ/dx)0
となります。点rp(xp、yp、zp)にp=qdの双極子があったとき、それが任意の点(x,y,z)につくるポテンシャルφ(x,y,z)は
・ φ(x,y,z)=(p・r)/4πεor3
=(1/4πεo)・p(z-zp)/{(x-xp)2+(y-yp)2+(z-zp)2}3/2
となります。点Pにある双極子の電場により原点にある双極子がもつエネルギは
・ U=p(dφ/dx)0=(p2/r3)(1-3 zp2/r2)
となります。双極子が立方格子状に分布している場合は、格子定数aとすると、整数i、j、kに対して、
・ (xp、yp、zp)=(ai、aj、ak)
となるので、エネルギは
・ U==p2/a3 ∑( i2+j2+k2) -5/2・(i2+j2+k2-3k2)
と表せます。和を取る際に(i、j、k)をサイクリックに入れ替えて3で割ると、分母は変わりませんが、
分子=1/3{(i2+j2+k2-3k2)+(k2+i2+j2-3j2)+(j2+k2+i2-3i2)}=0
となるので、U=0となります。したがってEi=0となります。
したがって、分子に働く電場の強さは
・ E=Eo+P/3εo
となります。これをロ-レンツの内部電界といいます。単位体積当たりの双極子数をNo、分子の分極率をαとすると、分極ベクトルPは
・ P=NoαεoE=Noαεo(Eo+P/3εo)
となります。これをPについて解くと
・ P=NoαεoEo/(1-Noα/3)
となります。これを電束密度DにあるPに代入すると
・ D=εoEo+P=εoEo+NoαεoEo/(1-Noα/3)
=(1+2Noα/3)/(1-Noα/3)・εoEo
一方
・ D=εEo=(ε/εo)εo Eo
なので
・ ε/εo=(1+2Noα/3)/(1-Noα/3)
となります。αについて解くと、双極子の分極率と屈折率の関係式
・ α=(3/No)(ε/εo-1)/(ε/εo+2)=(3/No)(n2-1)/(n2+2)
が得られます。これをクラジウス・モソッティの式(1879年)といいます。

それでは双極子ベクトルP(t0)
・ P(t0)=∫ρ(r’, t0)r’d3r’(t0=t-r/c)
から距離r離れた位置に観測される散乱波の電場E(r,t)が、
と書けることを証明します。ここでcは光速です。
電場と磁場は、電磁ポテンシャルφ、Aと
・ E=-gradφ-∂A /∂t
・ B=rot A
なる関係があります。電磁ポテンシャルφ、Aを用いたマクスウエルの方程式は
・ (△-1/c2∂2/∂t)φ=-ρ/ε0
・ (△-1/c2∂2/∂t)A=-μ0i
・ 1/c2・∂φ/∂t+divA=0 (Lorentz gauge)
・ 1/c2=ε0μ0
で与えられます。電磁ポテンシャルは、電荷密度ρと電流密度iに対して
・ φ(r,t)=(1/4πε0)∫ρ(r’,t-∣r-r’∣/c)/ ∣r-r’∣d3r’
・ A (r,t)=(μ0/4π)∫i(r’,t-∣r-r’∣/c)/ ∣r-r’∣d3r’
・ =(1/4πε0)1/c2∫i(r’,t-∣r-r’∣/c)/ ∣r-r’∣d3r’
と表すことができます。必ずしも容易ではありませんが、この定理は上式に代入すると解になっていることで確かめられます。物理学では証明に用いる定理が証明すべき命題より難しいことが時々あります。数学的には1/rがφに係るダランベシアン作用素のグリ-ン関数核なので、ソ-ス項と1/rの積の積分は電磁場方程式の解になるということです。よく知られた定理なので、ひとまずこれを認めましょう。

物理学では大抵の場合、厳密に積分するのは困難です。ここでは電気双極子近似を導入します。電子が存在している領域半径r’ に比べ、観測地点がずっと遠くにある(r’<<r)場合を想定しているので、
・ ∣r-r’∣≒r(1-r・r’/r)
・ 1/∣r-r’∣≒1/r・(1+r・r’/r)=1/r+O(r’/r)≒1/r
・ r=∣r∣=root(x2+y2+z2)
のように近似します。なぜなら
∣r-r’∣=root(∣r∣2-2r・r’+∣r’∣2) ≒ r (1-2r・r’/r)1/2≒r (1-r・r’/r)
だからです。さらにテ-ラ展開の1次までとると
・ ρ(r’,t-∣r-r’∣/c)≒ρ(r’,t-r /c+r・r’/cr) ≒ρ(r’,t0+r・r’/cr)
・ ≒ρ(r’,t0)+[dρ(r’,t0) /dt0]・(r・r’)/cr
となります。上式のρをφの式に代入すると、
・ φ(r,t)=(1/4πε0r)∫ρ(r’,t0) d3r’+(r/cr2)・(d /dt0)1/4πε0∫ρ(r’,t0)r’d3r’
となります。ここで第一項は
・ Q=∫ρ(r’,t0) d3r’
を含みますが、電荷Qは原子に束縛されており、時間的に変化しないので、無視できます。
・ P(t0)=∫ρ(r’, t0)r’d3r’
ですので、スカラ-ポテンシャルは、双極子ベクトルを用いて
・ φ(r,t)=(1/4πε0) (r /cr2)・(dP(t0) /dt0)
と書けます。同様にベクトルポテンシャルに関して、双極子近似を適用して展開すると
・ (4πε0) A (r,t)≒ (1/c2r)∫i(r’, t0+r・r’/cr ) d3r’
≒(1/c2r)∫i(r’, t0) d3r’+(1/c3r2)∫di(r’, t0)/dt0 (r・r’) d3r’
≒(1/c2r)∫i(r’, t0) d3r’ +O(1/c3)
となり第二項は無視できます。ここで断面積S、長さr’の導線を考えると、電流は
・ i(r’, t0)=1/S・dq/dt0・r’/r’=d(q/V)/dt0・r’=dρ/dt0・r’
と書けるので、
・ A (r,t)≒(1/4πε0) (1/c2r) (d/dt0)∫ρ(r’,t0)r’ d3r’
より、ベクトルポテンシャル Aも双極子ベクトルP(t0)を用いて
・ A (r,t)=(1/4πε0) (1/c2r) (dP(t0)/dt0)
と表せます。電場の表式に電磁ポテンシャルを代入すると
・(1/4πε0)E(r,t)=-gradφ-∂A /∂t
=-grad[(r /cr2)・(dP(t0) /dt0)]-∂/∂t[(1/c2r) (dP(t0)/dt0)]
となります。ところで第一項のgradのx微分を考えると、
(d/dx)(r /cr2)=ex /cr2-(2r /cr3) dr/dx=ex /cr2-2rx/cr4=O(1/r2)+O(1/r3)
の部分は、次のx微分の項
・ -(r /cr2)(d/dx)(dP(t0) /dt0)=-(r /cr2)(d(t-r/c)/dx)(d2P(t0) /dt02)
=-(r /cr2)(-x/cr)(d2P(t0) /dt02) ~ O(1/r)
に比べると十分遠方で早く小さくなるので、無視できることが分かります。結局
・ (1/4πε0)E(r,t)≒(r/cr) [(r /cr2)・(d2P(t0) /dt02)]-(1/c2r)d2P(t0) /dt02
・ =(1/c2r3){r [r・d2P(t0) /dt02] -(r・r) d2P(t0) /dt02 }
・ E(r,t)=(1/4πε0) (1/c2r3) r×(r×d2P(t0) /dt02)
により公式が得られます。最後の等式は、A=r、B=r、C=d2P(t0) /dt02とおいて恒等式
B(A・C)-(A・B)C=A×(B×C)
を適用して得ました。すこし難しくなってしまいましたが、双極子放射の公式が電磁気学の基本方程式から得られることを確かめました。次回は古典的な分極率の導出についてお話します。
太陽光の放射強度Iは、大気中を通過する際に散乱されて減衰します。散乱体の密度ρ[kg/m3]と散乱係数σ[m2/kg]を用いると、地表での放射強度をIoとすると、高度zでの放射強度Iは
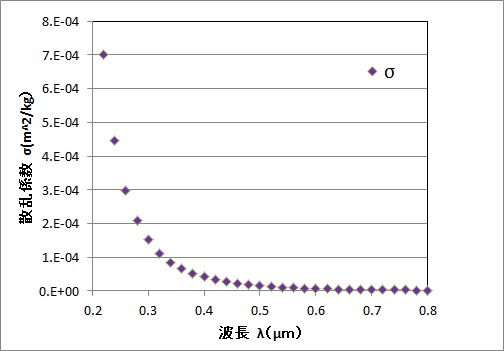
と表せます。波長λの光のレ-リ-散乱係数σRは、古典電磁気学的には
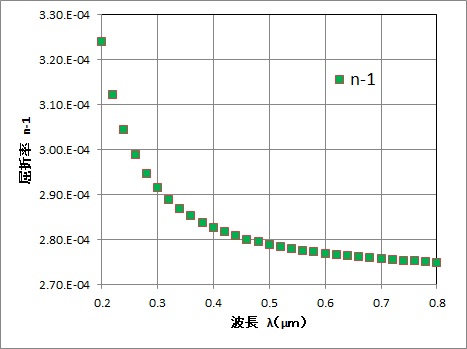
と表せます(1871年)。ここでNo[個/m3]は空気の分子数、nは空気の屈折率(=1.000292@1atm,0℃)です。
空気の屈折率(n-1)の波長依存性はEdlenの式を用いました。波長が大きくなると屈折率と散乱係数σRは減少します。
分子量Mwに対して、理想気体の状態方程式より
となります。ここでHは高さパラメ-タで、大気の厚さH=8kmとしました。減光率は
で求めました。減光率が小さいということは散乱され難いということです。
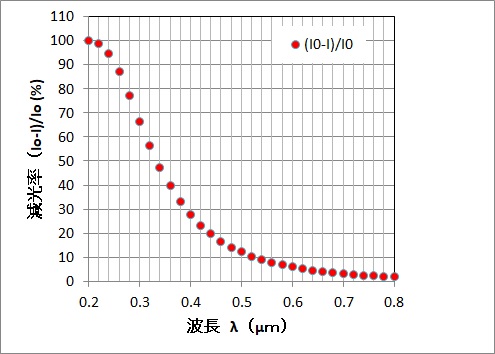
減光率は可視領域で波長が大きくなると、急速に減少します。近紫外領域(λ~0.3μm)では40%もの太陽光が失われます。青色光(λ~0.4μm)では30%、緑色光(λ~0.5μm)では12%、赤色光(λ~0.65μm)では4%、近赤外領域(λ~0.94μm)では1%しか失われません。様々な太陽高度と波長を考慮すると、大気に入射する平均太陽放射のうち13%がレイリ-散乱されているそうです。その半分が散乱光として地表面へ到達し、残り半分は宇宙空間へ放射されます。夕焼けのときは、8km以上の距離を太陽光が進むのでその間に青色光は殆ど散乱されてしまい、赤色光だけが届くことになります。

地球の空が青いのは、日光に含まれる波長の短い青色光が窒素分子に散乱されやすいからです。日没時に空が赤くなるのは、太陽光が大気を通過する距離が長くなり、空気分子の光散乱が増大し、青色光が届かず、赤色光のみが届くようになるからです。月面から見上げた空は黒色です。月には空気がないので、光散乱が起こらないからです。20世紀になるまで空が何故青いのか分かっていませんでした。空気のように透明な媒質が散乱体になるとは思いもよらないことでした。
レ-リ-(Rayleigh)散乱(1910年)
空気の分子のように光の波長の1/10以下の散乱体による散乱をレ-リ-散乱といいます。レ-リ-男爵の本名はジョン・ウイリアム・ストラットです。レ-リ-卿(英国)はアルゴンの発見者で、地震の表面波(レーリ-波)や黒体放射でも有名な物理学者です。レ-リ-散乱の強度は光波長の4乗に反比例します。このことは電磁気学の知識があれば理解できるので、後で解説したいと思います。
液体の分子濃度は気体の1000倍ありますが、液体の光散乱は、気体と比較して5~50倍程度しかありません。ガラスの光散乱も非常に弱いです。これは散乱体が稠密になると、任意の横方向において、散乱波が互いに打ち消し合う分子対が常に存在するためと思われます。光ファイバ-(石英ガラス)ではレ-リ-散乱の小さな波長帯(1.5μm帯)を使っています。
ミ-(Mie)散乱(1908年)
雲を形成する水滴は、太陽からの可視光の波長に比べて同程度ないしはそれより大きい粒子になっています。このような水滴に光が当たると、ミ-散乱が起こります。ミ-散乱では、可視光のどの波長も同じように散乱されますので、雲は白色に見えます。
ブスタフ・ミ-(独)は球形粒子による散乱の理論解析を行い、ミ-散乱は波長にほとんど依存せず、粒子寸法が光波長を越えると、散乱の波長依存性はなくなることを示しました。レ-リ-散乱は等方的ですが、ミ-散乱には異方性があります。ミ-散乱はアンテナやがん細胞の判別に用いられています。
虹(rainbow)
虹は、水滴内を太陽光が屈折反射することで、光が波長ごとに空間分解される現象です。主虹と副虹ができる理由を最初に解明したのはデカルトです。プリズムで太陽光をスペクトル分解して見せたのがニュ-トンです。虹は虫偏なのは、蛇が虫偏なのと同じ理由です。古代中国人は虹を空にアーチを架ける大蛇として見ていたからと言われています。
非弾性散乱
レ-リ-散乱とミ-散乱は光の波長が変化しない弾性散乱です。光の波長が変化する非弾性散乱には、ラマン散乱やブリルアン散乱があります。
ラマン(Raman)散乱(1928年)
ラマン散乱は分子の振動準位や回転準位の遷移に伴い、入射光とは異なる波長の光が散乱される現象です。ラマン散乱を利用して化学物質の判定を行うことができます。白色矮星の質量にチャンドラセカール限界質量があることを示したスブラマニアン・チャンドラセカ-ル(1932年)は、ラマン・チャンドラセカール(印)の叔父にあたります。
ブリルアン(Brillouin)散乱(1922年)
ブリルアン散乱は光と音響子などの凖粒子との相互作用による光散乱です。ブリルアン散乱は光ファイバの歪や温度を検知するのに使われます。レオン・ブリルアン(仏)は量子力学のWKB近似や固体物理のブリルアンゾ-ンでも有名な物理学者です。
理想気体の静力学平衡の式は
・ dP=-(MairP/RT)gdz=-(g/RairT)・Pdz
でした。よって
・ dP/P=-(g/RairT)dz
となります。
1)温度が一定の場合、上式を積分すると
・ ln(P/P0)=-(g/RairT) (z-z0)=-(z-z0)/H
・ P=P0exp(-(z-z0)/H)
温度を-18℃(255K)とすると
・ H=RairT/g=287[J/KKg]・255K/ 9.8[m/ss]=7.5km
・ P0=1013hPa、Z0=0m
が得られます。
2)上空の温度が気温減率で減少する場合
・ T(z)=T0-Γz、Γ=6.5K/100m
なので
・ dP/P=-(g/ RairT(z))dz=-(g/Rair)・dz/( T0-Γz)
を積分すると
・ ln(P/P0)=(g/RairΓ)・ln((T0-Γz)/T0)
ですから、気圧は
・ P=P0((T0-Γz)/T0)^ (g/RairΓ) 0<z<10km
となります。15℃=288Kでは
・ g/RairΓ=9.8[m/ss]/ 287[J/KKg]0.0065[K/m]=5.25
・ P(z)=1013[hPa]((1-6.5[K/km]・z[km]/288[K])^5.25 0<z<10km
・ P(z=5km)=1013・(1-6.5・5/288)^5.25=1013・0.887^5.25=1013・0.533=540.3hPa
・ P(z=10km)=1013(1-6.5・10/288)^5.25=1013・0.774^5.25=1013・0.261=264.5hPa
となります。
3)10km以上の上空の場合
10kmでの気温 -55℃(218K)が一定となるので
・ H1=RairT/g=287[J/KKg]・218K/ 9.8[m/ss]=6.38km
・ P=246.5[hPa]・exp(-(z-10[km])/6.38[km]) 10km<z
と近似することができます。
Pv(T)の関数形
飽和水蒸気圧Pvの温度依存性を求めてみましょう。
・ dPv=QL/ TV・dT
を状態方程式
・ Pv=RvT/V、 Rv=461[J/Kg]
で辺々を割ると
・ dPv/ Pv=(QL/ TV・dT)/ (RvT/V)=(QL/ Rv)(dT /T^2)
となります。これを積分すると、
・ ln(Pv/Pv0)=-(QL/ Rv)(1/T-1/T0)
これをPvについて解くと
・ Pv=6.11・exp{-(QL/ Rv)(1/T-1/T0)} [hPa] for 273K
が得られます。つまり飽和水蒸気圧Pvは、圧力に依存せずに、温度だけの関数になります。
クラジウス・クラペイロンの式
液体の水と平衡状態にある飽和水蒸気圧Pvの温度係数(dPv/dT)は、潜熱と相変化に伴う体積変化と転移温度に関して、以下の関係
・ dPv/dT=QL/ T(Vgas-Vliquid)≒QL/ TVgas
が成り立ちます。これはクラジウス・クラペイロンの式と呼ばれる式です。Rv=R/Mwater、
・ dPv/dT=(QL/ T)(Pv/PvVgas)=(QL/ T)(Pv/RvT)=(QL/ T)(Pqs/0.622)/RvT
・ 分母=1+(0.622 QL /CpP) (dPv/dT)=1+(0.622 QL /CpP) (QL/ T^2) (Pqs/0.622Rv)=1+qsQL^2/ CpRvT^2
湿潤断熱減率は
・ dT/dz=-g/Cp{1++QL・qsMair/ RT)}/{1+qsQL^2・Mwater/ CpRT^2}
となります。
クラペイロンの式は、水蒸気と水が共存する系のPV線図において、温度差dTの2つの等温変化と水と水蒸気の相変化を有するサイクルにおいて、相変化で生じる潜熱QLに対してなされる仕事
・ dW=(Vgas-Vliquid)dPv
の割合がカルノ-効率に等しい条件
・ dW/ QL=dT/ T
を表しています。
湿潤断熱減率を求める
温度10℃(=283K)、気圧P=700hPaで飽和している空気塊の湿潤断熱減率を求めてみましょう。データ表から、10℃、700hPaでの飽和混合比は、qs=11.13×10^-3[Kg/Kg]でした。飽和蒸気圧データから、飽和蒸気圧は12.28hPa(10℃)、10.73hPa(8℃)でした。
湿潤断熱減率
・ dT/dz=-g/Cp{1+QL(qsMair/RT)}/{1+(0.622 QL /CpP) (dPv/dT)}
の因子は
・ g/Cp=9.8[m/s^2]/1004[J/KKg]=0.0098[K/m]=9.8[K/km]
となります。分子の中は
・ QL(qsMair/RT)=2.5×10^6[J/Kg]・11.13×10^-3[Kg/Kg]・29×10^-3[Kg]/8.31[J/KKg]/283[K]=0.3425
分母の中は
・ 0.622 QL /CpP=0.622・2.5×10^6[J/Kg]/ 1004[J/KKg]・70000[Pa]=0.0221[K/Pa]
デ-タ表から
・ dPv/dT=(12.28-10.73)/(10-8)=1.55/2=0.775[hPa/K]=77.5[Pa/K]
以上を代入すると、湿潤断熱減率は
dT/dz=-9.8[K/km]・[1+0.3425]/[1+0.0221・77.5]=-9.8[K/km]・0.4945=-4.85[K/km]
つまり約0.5℃/100mであることが示されます。
クラペイロンの式を用いた場合には、
dPv/dT=PQLqs/ 0.622RvT^2
=700[hPa]・2.5×10^6[J/Kg]・11.13×10^-3[Kg/Kg]/{287[J/KKg]・283[K]^2}
=84.73[Pa/K]
となるので、
dT/dz=-9.8[K/km]・[1+0.3425]/[1+0.0221・84.73]=-9.8[K/km]・0.467=-4.58[K/km]
なる0.5℃/100mに近い値が得られました。
乾燥断熱減率の導出
断熱過程と静力学平衡の式は比熱比をγ、空気分子1個の質量をMairとすると、
・ dT/T=(γ-1)/γ・dP/P (断熱過程)
・ dP=-(MairP/RT)gdz (静力学平衡)
と表せました。この式からdPを消去すると
・ dT/T=-(γ-1)/γ・(Mair・g/RT)dz
つまり乾燥断熱減率を表す式
・ dT/dz=-(γ-1)/γ・Mair・g/R
が得られます。空気1モルの重さMは0.029(Kg/mol)ですから
・ dT/dz=-2/7・0.029(Kg/mol)・9.8(m/ss)/ 8.3(J/Kmol)=-9.8℃/km
が得られます。実は空気の定圧比熱は
・ Cp=γ/(γ-1)・R/Mair=(7/2)・287[J/KKg]=1004[J/KKg]
なので、乾燥断熱減率は
・ dT/dz=-g/Cp=-9.8(m/ss)/ 1004[J/KKg]=-9.8℃/km
と表されます。これはおよそ1℃/100mの温度勾配を意味しています。つまり山の斜面で空気塊が押上げらえると、水蒸気が水滴になるまで、100mにつき1℃の割合で空気塊の温度が減少することを示しています。
湿潤断熱減率の導出
乾燥断熱減率はg/Cpであることが分かりました。水滴を含む空気の湿潤断熱減率を求めましょう。湿潤断熱減率を求めるためには、飽和混合比を用います。水蒸気の質量をmv、乾燥空気の質量をmdとすると、飽和混合比qsは
・ qs=mv/md
によって定義されます。qsは圧力と温度に依存しています。乾燥空気と水蒸気の状態方程式はそれぞれ
・ PdV=(md/Mair)RT
・ PvV=(mv/Mwater)RT
で表されます。Pv/P≒3%なので
・ qs=(Mwater/Mair)Pv/Pd=(18/29)Pv/(P-Pv)≒0.622・Pv/P
と表されます。この関係式が重要です。飽和混合比qsは水蒸気圧Pvと全圧力Pの比になっています。両辺の対数を取って微分すると
・ dqs/qs=dPv/Pv-dP/P
となります。後で示しますがPv=Pv(T)、つまりPvは温度だけに依存します。飽和混合比の変化量は
・ dqs=(qs /Pv) (dPv/dT)dT-(qs/P)dP=(0.622 /P) (dPv/dT)dT-(qs/P)dP
と変形できます。湿った空気塊が上昇すると冷えて水滴が発生し、水蒸気圧が低下します。
水蒸気は水滴になるときに凝縮熱QL[J/Kg]を出します。発熱量は
・ d’Q=-QL・dqs=-QL・{(0.622 /P) (dPv/dT)dT-(qs/P)dP}
で与えられます。一方、第一法則は、気体の質量m当たりのエネルギの保存を考えると
・ d’Q=CpdT-(V/m)dP
ですから、両式のd’Qを消去し、dzで両辺を割ると、
・ -QL (0.622 /P) (dPv/dT)(dT/dz)+QL(qs/P)(dP/dz)=Cp(dT/dz)-(V/m)(dP/dz)
・ -Cp{1+(0.622 QL /CpP) (dPv/dT)} (dT/dz)=-{V/m+QL(qs/P)}(dP/dz)
となります。静力学平衡の式
・ dP/dz=-g(m/V)
を代入すると、右辺は
右辺=-{V/m+QL(qs/P)} g(m/V)=g{1+QL(qsm/PV) }=-g{1+QL(qsMair/RT) }
となります。ここでPV=(m/Mair)RTを用いました。乾燥空気の状態方程式を用いるのはよい近似となります。従って湿潤断熱減率は
・ dT/dz=-g/Cp{1+QL(qsMair/RT)}/{1+(0.622 QL /CpP) (dPv/dT)}
と表されます。g/Cpは乾燥空気の断熱減率でした。ここで分母にある(dPv/dT)の値は、飽和水蒸気圧の温度依存性デ-タから求めることができますが、次のように理論的に求めることもできます。
断熱過程での温度と圧力の関係
(T,P)表示の熱力学第一法則
・ d’Q=CpdT-VdP
に理想気体の状態方程式V=RT/Pを代入すると、
・ d’Q=CpdT-(RT/P)dP=0 (断熱過程)
となります。空気の熱伝導率は小さいので空気塊の上昇は断熱過程(d’Q=0)と考えられます。断熱過程の場合、R=Cp-Cvより
・ dT/T=(R/Cp)dP/P=(γ-1)/γ・dP/P
と書けます。ここでγ=Cp/Cvを比熱比といいます。2原子分子の場合、
・ γ=Cp/Cv=(7R/3)/(5R/3)=7/5
なので、(γ-1)/γ=2/7となります。上式を積分すると
・ lnT=(γ-1)/γlnP+const
・ T/P^(γ-1)/γ=一定
となります。これは圧力が下がると温度が下がること表しています。
静力学平衡
断面積A、高さdZの空気塊に働く圧力差と重力は釣り合っています。空気塊の質量をm、重力加速度をgとすると、
・ ma=A(dP/dz)dZ-mg=0
ですから、V=AdZとして、静力学平衡式は
・ dP=-(m/V)gdz
となります。気体分子1個の質量をMとすると、気体の状態方程式は
・ PV=(m/Mair)RT → m/V=MP/RT
となります。密度m/VはPとTに依存しています。密度を消去すると、
・ dP=-(MairP/RT)gdz
理想気体の静力学平衡の式が得られます。
理想気体の状態方程式は
・ PV=RT
で表されます。ここでRは気体定数
・ R=8.314[J/Kmol]
でした。Rは1モルの気体を1K上げるのに必要な熱量です。乾燥空気の分子量はMair=29g/molですから、気象学では乾燥空気の気体定数として
・ Rd=8.314[J/Kmol]/0.0029[kg/mol]=287[J/KKg]
を用います。同様に、水蒸気の気体定数は、Mwater=18g/molなので
・ Rv=8.314[J/Kmol]/0.0018[kg/mol]=461[J/KKg]
となります。両者の比は
・ ε=Rd/Rv=287/461=0.622
となります。
(T,V)表示の熱力学第一法則
熱力学の第一法則は「外部から加えられた熱量d’Qは、内部エネルギの増加量dUと外部にする仕事dWの和で与えられる」と表現されます。
・ d’Q(熱量)=dU(内部エネルギ)+dW(仕事)
理想気体の内部エネルギは、気体の分子間相互作用を無視するために体積に依らないので
・ dU=(dU/dT)v dT+(dU/dV)T dV ≒ (dU/dT)v dT
と書けます。定積比熱
・ Cv=(d’Q/dT)v=(dU/dT)v
を用いると、(T,V)系の熱力学第一法則は
・ d’Q=CvdT+PdV
と表せます。外部から加えた熱は、気体の内部エネルギの上昇と体積膨張によって気体が外部にする仕事の和に等しいことを表しています。ちなみにd’Qのプライムは完全微分ではないことを示すものです。
(T,P)表示の熱力学第一法則
内部エネルギU(T,V,P)は3変数の関数ですが、PV=RTの状態方程式があるので、独立な変数は2つです。先ほどの式は第一法則を2つの独立変数(T,V)で表したものですが、(T,P)を用いて表すこともできます。PV=RTから、
・ RdT =d(PV)=PdV+VdP
が成り立つので、dVをdPとdTで表すことができます。
・ d’Q=CvdT+PdV=(Cv+R)dT-VdP
より、第一法則は(T,P)表示で
・ d’Q=CpdT-VdP
とも書き表せます。ここで定圧比熱
・ Cp≡(d’Q/dT)p=Cv+R (Mayer’s relation)
を導入しました。乾燥空気の定圧比熱は
・ Cp=(7/2)・8.314[J/Kmol]/0.0029[kg/mol]=(7/2)・287[J/KKg]=1004[J/KKg]
です。あるいはエンタルピH=U+PVなる量を用いて、(T,P)表示の第一法則
・ d’Q=dU+PdV=d(U+PV)-VdP=dH-VdP=(dH/dT)pdT-VdP=CpdT-VdP
を導くこともできます。少し分かりにくい形になってしまいますが、圧力と温度は計測や制御がしやすいので、化学系の研究室では、(T,P)表示がよく用いられます。
フェーン(Föhn)とはドイツ語でアルプスの北麓に吹き降ろす局地風のことだそうです。フェーン現象とは、高山の斜面にあたった湿った空気が雨を降らして山を越え、暖かくて乾いた下降気流となってその付近の気温を上昇させる現象のことです。例えば、標高2000mの山を越える場合、平地で25℃の湿った空気は山頂で15℃となり、山を越えた平地では乾燥空気は35℃になります。その理由は、空気塊が引き上げられる場合、水滴を含むような湿った空気の温度は0.5℃/100m(湿潤断熱減率)の割合で減少しますが、水滴を含まない乾いた空気の温度は1℃/100m(乾燥断熱減率)の割合で減少するからです。つまり山頂から降りてくる乾燥空気の場合は逆に、1℃/100mの割合で増加するからです。
気温減率とは
上空に行くほど気温は低くなります。その低下割合は0.65℃/100mで、気温減率と呼ばれています。登山家は気温減率を用いて山頂の気温を推定します。気温減率はフェーン現象を引き起こす断熱減率とは異なります。地上の平均温度は10℃、10km上空の対流圏での温度は-55℃程度なので、気温減率は温度差65℃を10kmで割った値になります。上空の寒気団の温度によって日々の気温減率は変動します。温度差が大きい方が、大気が不安定になり、対流が活発になります。
ところで乾燥断熱減率や湿潤断熱減率の値はどのようにして求めたのでしょうか?
まず乾燥断熱減率について考えてみましょう。乾燥断熱減率は断熱過程の熱力学第一法則と静力学平衡から求められます。断熱過程の熱力学第一法則は、微小な温度変化dTと体積変化dVの関係を与えます。第一法則の表示を(T,V)系から(T,P)系に変換することで、温度変化dTと圧力変化dPの関係に書き換えることができます。静力学平衡は空気塊の鉛直方向の微小長さdzと圧力変化dPの関係を与えます。従って両者から、温度変化dTと微小長さdzの比である乾燥断熱減率が求まります。