＜マンゴルトの明示公式＞

前回チェビシェブ関数の積分表示

   Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} ζ'(s)/ζ(s)・x^s/s ds

を求めました。今回は積分を実行し、マンゴルトの明示公式を導出します。

　f_x(s)＝ζ'(s)/ζ(s)・x^s/s

とおくと

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds＝－1/2πi・∫_C1 f_x(s)ds

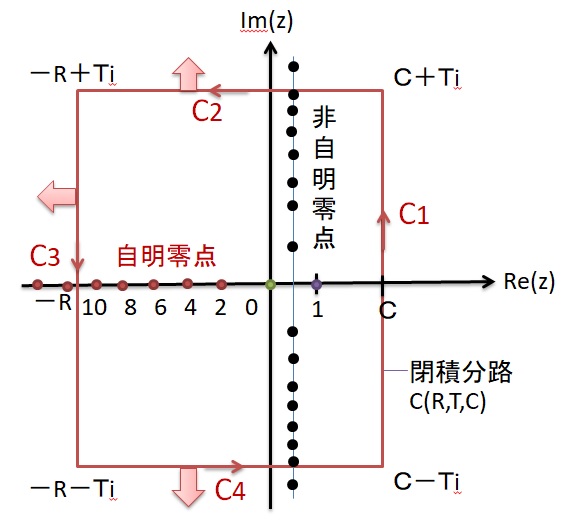
となります。この複素積分を閉曲線C(c,T,R）

　C(c,T,R)＝C_{1[c－Ti、c＋Ti]}＋C_{2[c+Ti、－R＋Ti]}＋C_{3[－R＋Ti、－R －Ti]}＋C_{4[－R－Ti、c－Ti]}

に拡張すると、

　lim_[R,T→∞]∫_C2 f_x(s)ds＝lim_[R,T→∞]∫_C3 f_x(s)ds＝lim_[R,T→∞]∫_C4 f_x(s)ds＝0

となるので、

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds

　　　　＝－1/2πi・lim_[R,T→∞]∫_C(c,T,R）f_x(s)ds

となります。閉曲線内に含まれるf_x(s)の極の留数を計算すれば、Ψ^*(x)を求めることができます。

＜マンゴルトの明示公式＞

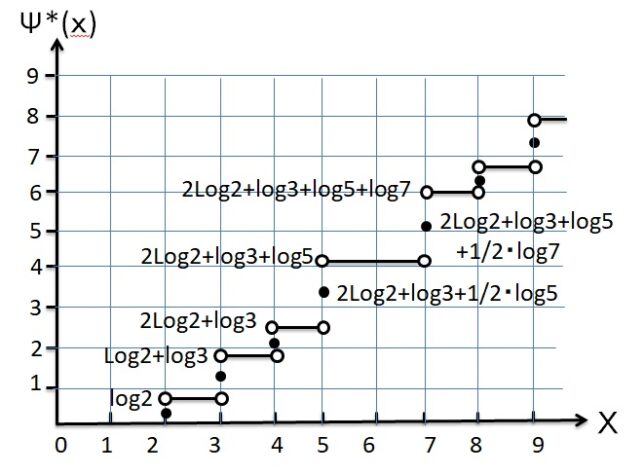
チェビシェフの素数pの階段関数

　Ψ^*(x)＝Σ[n≦x]Λ(n)＝Σ[p^m≦x] log(p)

に関して

　Ψ^*(x)＝x－1/2・log(1－x^－2)－log 2π－Σ’_ρ∊Z0x^ρ/ρ

がなりたつ。ここでZ₀＝｛ｓ｜ζ(s)＝0なる非自明な零点｝である。マンゴルトの明示公式は、素数の分布を表す階段関数Ψ^*(x)がゼ－タ関数の非自明な零点の和を含むｘの解析関数によって書かれているという不思議な公式です。

閉曲線内の

　f_x(s)＝ζ'(s)/ζ(s)・x^s/s

の零点は、ρ＝1、－2n、0、ρ_iの4種類あります。

まずζ'(s)/ζ(s)の留数を考えます。

　ζ(s)～1/(s－1)+・・

　ζ'(s)～－1/(s－1)²+・・

　ζ'(s)/ζ(s)～－1/(s－1)+・・

なので、極をρとすると、位数Ord(ζ,ρ)について

　Res(ζ’/ζ,ρ)＝Ord(ζ,ρ)

が成り立ちます。偏角の原理より、留数は

　Res(ζ'(s)/ζ(s)・x^s/s,ρ)＝Ord(ζ,ρ) x^ρ/ρ

となります。

1）s＝1の留数

　Ord(ζ,1)＝－1となります。

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝1)＝Ord(ζ,1) x¹/1＝－x

2）s＝－2nの留数

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝－2n)＝Ord(ζ,1) x^－2n/(－2n)

R→∞でN→∞となるので

　－lim_[N→∞]Σ_n＝1～N x^－2n/(－2n)＝1/2・log(1－x^－2)

3）s＝0の留数

　　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝0)＝ζ'(0)/ζ(0)＝log(2π)

　　ζ(0)＝－1/2、ζ’(0)＝－1/2・log(2π)

4）ｓの非自明な零点ρ_iの留数

　Res(ζ'(s)/ζ(s)・x^s/s,ρ＝ρ_i)＝Ord(ζ,ρ_i) x^ρi /ρ_i

T→∞でN→∞となるので

　lim_[N→∞]Σ_i＝1～N Ord(ζ,ρ_i) x^ρi /ρ_i＝Σ’_ρ∊Z0 x^ρ /ρ

Σ’_ρ∊Z0は非自明な零点ρでの位数がｍの場合ｍ回和をとると言う意味です。

以上から、マンゴルトの明示公式

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} f_x(s)ds

　　　　＝－1/2πi・lim_[R,T→∞]∫_C(c,T,R）f_x(s)ds

　　　　＝－1/2πi・2πi・（－x＋1/2・log(1－x^－2)＋log 2π＋Σ’_ρ∊Z0 x^ρ /ρ）

　　　＝x－1/2・log(1－x^－2)－log 2π－Σ’_ρ∊Z0 x^ρ /ρ

が成り立ちます。

偏角原理とは、z=z₀でm位の特異点をもちそれ以外で正則な関数f(z)に関して

　Res(f’/f,z₀)＝Ord(f,z₀)＝m

が成り立つ定理です。f(z)は、z=z₀で特異点をもたない正則関数g(z)を用いて

　f(z)＝(z－z₀)^m・g(z)

と書けます。このとき、

　f'(z) /f(z)＝[m(z－z₀)^m－1・g(z)＋(z－z₀)^m・g'(z)]/ (z－z₀)^m・g(z)

　　　　　＝m/(z－z₀)＋g'(z)/ g(z)

なので、f'(z) /f(z)はz＝z₀で1位の極を持つことがわかり

　Res(f’/f,z₀) ＝m＝Ord(f,z₀)

が成り立ちます。

＜マンゴルト関数Λ(n)とチェビシェフ関数Ψ(x)＞

自然数nに対して、マンゴルト関数Λ(n)を

　　Λ(n)＝log(p)　if　n＝p^m, 　otherwise 0

と定義します。ここでpは素数です。具体的には

　Λ(1)＝0、Λ(2)＝log2、Λ(3)＝log3、Λ(4)＝Λ(2²)＝log2、Λ(5)＝log5、

　Λ(6)＝Λ(2・3)＝0、Λ(7)＝log7、Λ(8)＝Λ(2³)＝log2、Λ(9)＝Λ(3²)＝log3、

　Λ(10)＝Λ(2・5)＝0、Λ(11)＝log11、Λ(12)＝Λ(2・2・3)＝0、・・・

です。単一の素数のべき乗でのみΛ値がゼロではありません。

実数xに対して、チェビシェフ関数Ψ(x)を

　　Ψ(x)＝Σ_[n≦x]Λ(n)＝Σ_[p^m_≦x] log(p)

と定義します。ここでpは素数です。Σ_[p^m≦x]は、x以下の素数pの冪乗となっている素数pで和をとることを意味します。Ψ(x)は階段関数です。

ｘ＝5とすると

　　Ψ(5)＝Λ(1)＋Λ(2)＋Λ(3)＋Λ(4)＋Λ(5)＝0＋log2＋log3＋log2＋log5

となります。Ψ(x)のステップアップする点で、ステップアップ部分の中点をとる関数をΨ^*(x)と書きます。

　　Ψ^*(5)＝log2＋log3＋log2＋1/2・log5

となります。Ψ^*(x)では最後の項が1/2倍になります。ｘ＝9の場合は

　　Ψ(9)＝Λ(1)＋Λ(2)＋Λ(3)＋Λ(4)＋Λ(5)＋Λ(6)＋Λ(7)＋Λ(8)＋Λ(9)

　　　　＝0＋log2＋log3＋log2＋log5＋0＋log7＋log2＋log3

　　Ψ^*(9)＝log2＋log3＋log2＋log5＋log7＋log2＋1/2・log3

となります。ｘが素数のべき乗でない場合は、両関数は等しくなります。例えば

　　Ψ(1000)＝Ψ(997)＝Ψ^*(1000)

に注意して下さい。

ゼ－タ関数ζ(s)

・ζ(s)＝Σ_n＝1～∞ 1/n^s＝Π_p∊P [1－1/p^s]^－1

に関して、

　ζ'(s)/ζ(s)＝－Σ_n＝1～∞ Λ(n)/n^s

となることを示します。

　ζ'(s)/ζ(s)＝(logζ(s))’＝－(Σ_p∊P log [1－1/p^s])’

です。ここで、テーラ－展開

　log(1－x)＝－Σ_n＝1～∞(xⁿ/n)

を用いると、

　log [1－1/p^s]＝－Σ_n＝1～∞(p^－ns／n)

なので、ｓで微分すると

　ζ'(s)/ζ(s)＝(logζ(s))’＝Σ_p∊PΣ_n＝1～∞ (p^－ns／n)’

となります。ここで

　(p^－ns／n)’＝ (e^{－nslog p}／n)’＝－nlog p・p^－ns／n＝－log p・p^－ns

に注意すると、

　－ζ'(s)/ζ(s)＝Σ_p∊PΣ_n＝1～∞log p・p^－ns

　　　　　＝Σ_p∊P (log p／p^s＋log p／p^2s＋log p／p^3s＋log p／p^4s＋・・・)

　　　　　＝log 2／2^s＋log 3／3^s＋log 5／5^s＋log 7／7^s＋・・・

            　　　＋log 2／2^2s ＋log 3／3^2s＋log 5／5^2s＋log 7／7^2s＋・・・

　　　　　　＋log 2／2^3s＋log 3／3^3s＋log 5／5^3s＋log 7／7^3s＋・・・

　　　　　　＋log 2／2^4s＋log 3／3^4s＋log 5／5^4s＋log 7／7^4s＋・・・

　　　　　＝log 2／2^s＋log 3／3^s＋log 2／4^s＋log 5／5^s＋log 7／7^s＋log 2／8^s

　　　　　　＋log 3／9^s＋log 11／11^s＋log 13／13^s ＋log 2／16^s＋・・・

　　　　　＝Σ_n＝1～∞ Λ(n)/n^s

が得られました。一般に

　D(s)＝Σ_n＝1～∞ a_n/n^s

なる級数をディリクレ級数（Series）といいます。同じ数列a_nに対する階段関数を

　S(x)＝Σ^*_n≦x a_n

とします。ここでΣ^*はステップアップ部分は中点をとることを意味します。D(s)とS(x)はペロンの公式で結び付けられています。

＜ペロンの公式＞

D(s)＝Σ_n＝1～∞ a_n/n^sがRe(s)＞1で絶対収束するとき、c＞1に対して、

　S(x)＝1/2πi・∫_{[c－i∞、c＋i∞]} D(s)x^s/s ds

が成り立つ。これを示します。

Re(s)＞0において、

　s∫_[n,∞] x^－s－1dx＝s[x^－s /(－s)] _[n,∞]＝1/n^s

が成り立ちます。するとディリクレ級数D(s)はRe(s)＞1で絶対収束しており、

　D(s)＝Σ_n＝1～∞ a_n/n^s＝sΣ_n＝1～∞∫_[n,∞] a_n x^－s－1dx

　　　＝s(∫_[1,∞] a₁ x^－s－1dx＋∫_[2,∞] a₂ x^－s－1dx＋∫_[3,∞] a₃ x^－s－1dx＋・・・)

　　　＝s(∫_[1,2] a₁ x^－s－1dx＋∫_[2,3] (a₁＋a₂) x^－s－1dx＋∫_[3,4] (a₁＋a₂＋a₃) x^－s－1dx＋・・・)

　　　＝s・∫_[0,∞] S(x)x^－s－1dx

となります。

ここで関数f(x)に対するメリン変換M_f(s)を

　　M_f(s)＝∫_[0,∞] f(x)x^s－1dx

と定義します。すると

　D(s)/s＝M_S(－s)

と表せます。逆メリン変換M^－1[・]

　M^－1[M_f(s)] (x)＝1/2πi・∫_{[c－i∞、c＋i∞]} M_f(s)x^－s ds＝f(x)

を用いると、f(x)をS(x)に置き換えて

　S(x)＝1/2πi・∫_{[c－i∞、c＋i∞]} M_S(s)・x^－s ds

　　　＝1/2πi・∫_{[c－i∞、c＋i∞]} M_S(－s)・x^s ds

　　　＝1/2πi・∫_{[c－i∞、c＋i∞]} D(s)/s・x^s ds

が得られました。結局

　－ζ'(s)/ζ(s)＝Σ_n＝1～∞ Λ(n)/n^s＝D(s)

a_n＝Λ(n)のときのディリクレ級数D(s)になります。

Λ(n)に対する階段関数はΨ^*(x)でした。

　S(x)＝Σ^*_n≦x a_n＝Σ^*_n≦xΛ(n)＝Ψ^*(x)

よって、ペロンの公式より、c＞1に対して

　Ψ^*(x)＝－1/2πi・∫_{[c－i∞、c＋i∞]} ζ'(s)/ζ(s)・x^s/s ds

が成り立ちます。　次回はこの複素積分を実行し、マンゴルトの明示公式を導出します。