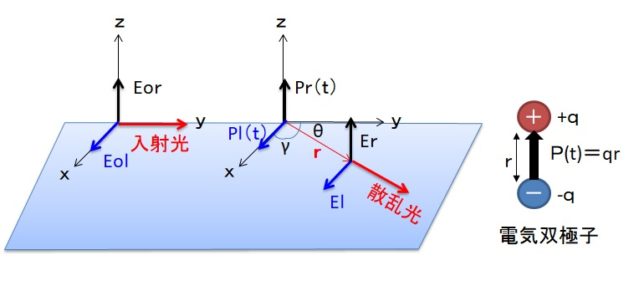
それでは双極子ベクトルP(t0)
・ P(t0)=∫ρ(r’, t0)r’d3r’(t0=t-r/c)
から距離r離れた位置に観測される散乱波の電場E(r,t)が、
- E(r,t) =(1/4πε0)(1/ c2r3)・r×[r×∂2P(t0)/∂t02]
と書けることを証明します。ここでcは光速です。
電場と磁場は、電磁ポテンシャルφ、Aと
・ E=-gradφ-∂A /∂t
・ B=rot A
なる関係があります。電磁ポテンシャルφ、Aを用いたマクスウエルの方程式は
・ (△-1/c2∂2/∂t)φ=-ρ/ε0
・ (△-1/c2∂2/∂t)A=-μ0i
・ 1/c2・∂φ/∂t+divA=0 (Lorentz gauge)
・ 1/c2=ε0μ0
で与えられます。電磁ポテンシャルは、電荷密度ρと電流密度iに対して
・ φ(r,t)=(1/4πε0)∫ρ(r’,t-∣r-r’∣/c)/ ∣r-r’∣d3r’
・ A (r,t)=(μ0/4π)∫i(r’,t-∣r-r’∣/c)/ ∣r-r’∣d3r’
・ =(1/4πε0)1/c2∫i(r’,t-∣r-r’∣/c)/ ∣r-r’∣d3r’
と表すことができます。必ずしも容易ではありませんが、この定理は上式に代入すると解になっていることで確かめられます。物理学では証明に用いる定理が証明すべき命題より難しいことが時々あります。数学的には1/rがφに係るダランベシアン作用素のグリ-ン関数核なので、ソ-ス項と1/rの積の積分は電磁場方程式の解になるということです。よく知られた定理なので、ひとまずこれを認めましょう。

物理学では大抵の場合、厳密に積分するのは困難です。ここでは電気双極子近似を導入します。電子が存在している領域半径r’ に比べ、観測地点がずっと遠くにある(r’<<r)場合を想定しているので、
・ ∣r-r’∣≒r(1-r・r’/r)
・ 1/∣r-r’∣≒1/r・(1+r・r’/r)=1/r+O(r’/r)≒1/r
・ r=∣r∣=root(x2+y2+z2)
のように近似します。なぜなら
∣r-r’∣=root(∣r∣2-2r・r’+∣r’∣2) ≒ r (1-2r・r’/r)1/2≒r (1-r・r’/r)
だからです。さらにテ-ラ展開の1次までとると
・ ρ(r’,t-∣r-r’∣/c)≒ρ(r’,t-r /c+r・r’/cr) ≒ρ(r’,t0+r・r’/cr)
・ ≒ρ(r’,t0)+[dρ(r’,t0) /dt0]・(r・r’)/cr
となります。上式のρをφの式に代入すると、
・ φ(r,t)=(1/4πε0r)∫ρ(r’,t0) d3r’+(r/cr2)・(d /dt0)1/4πε0∫ρ(r’,t0)r’d3r’
となります。ここで第一項は
・ Q=∫ρ(r’,t0) d3r’
を含みますが、電荷Qは原子に束縛されており、時間的に変化しないので、無視できます。
・ P(t0)=∫ρ(r’, t0)r’d3r’
ですので、スカラ-ポテンシャルは、双極子ベクトルを用いて
・ φ(r,t)=(1/4πε0) (r /cr2)・(dP(t0) /dt0)
と書けます。同様にベクトルポテンシャルに関して、双極子近似を適用して展開すると
・ (4πε0) A (r,t)≒ (1/c2r)∫i(r’, t0+r・r’/cr ) d3r’
≒(1/c2r)∫i(r’, t0) d3r’+(1/c3r2)∫di(r’, t0)/dt0 (r・r’) d3r’
≒(1/c2r)∫i(r’, t0) d3r’ +O(1/c3)
となり第二項は無視できます。ここで断面積S、長さr’の導線を考えると、電流は
・ i(r’, t0)=1/S・dq/dt0・r’/r’=d(q/V)/dt0・r’=dρ/dt0・r’
と書けるので、
・ A (r,t)≒(1/4πε0) (1/c2r) (d/dt0)∫ρ(r’,t0)r’ d3r’
より、ベクトルポテンシャル Aも双極子ベクトルP(t0)を用いて
・ A (r,t)=(1/4πε0) (1/c2r) (dP(t0)/dt0)
と表せます。電場の表式に電磁ポテンシャルを代入すると
・(1/4πε0)E(r,t)=-gradφ-∂A /∂t
=-grad[(r /cr2)・(dP(t0) /dt0)]-∂/∂t[(1/c2r) (dP(t0)/dt0)]
となります。ところで第一項のgradのx微分を考えると、
(d/dx)(r /cr2)=ex /cr2-(2r /cr3) dr/dx=ex /cr2-2rx/cr4=O(1/r2)+O(1/r3)
の部分は、次のx微分の項
・ -(r /cr2)(d/dx)(dP(t0) /dt0)=-(r /cr2)(d(t-r/c)/dx)(d2P(t0) /dt02)
=-(r /cr2)(-x/cr)(d2P(t0) /dt02) ~ O(1/r)
に比べると十分遠方で早く小さくなるので、無視できることが分かります。結局
・ (1/4πε0)E(r,t)≒(r/cr) [(r /cr2)・(d2P(t0) /dt02)]-(1/c2r)d2P(t0) /dt02
・ =(1/c2r3){r [r・d2P(t0) /dt02] -(r・r) d2P(t0) /dt02 }
・ E(r,t)=(1/4πε0) (1/c2r3) r×(r×d2P(t0) /dt02)
により公式が得られます。最後の等式は、A=r、B=r、C=d2P(t0) /dt02とおいて恒等式
B(A・C)-(A・B)C=A×(B×C)
を適用して得ました。すこし難しくなってしまいましたが、双極子放射の公式が電磁気学の基本方程式から得られることを確かめました。次回は古典的な分極率の導出についてお話します。