<ルジャンドルの2倍公式の証明>
Γ(2s)=22s-1/π1/2・Γ(s) Γ(s+1/2)
を証明する。
今、B(x,y)=Γ(x)Γ(y)/Γ(x+y) より
B(x,1/2)=Γ(x)Γ(1/2)/Γ(x+1/2)
B(x,x)=Γ(x)2 /Γ(2x)
が成り立つ。先ほど証明された式
B(x,1/2)=22x-1B(x,x)
に代入すると、
Γ(x)Γ(1/2)/Γ(x+1/2)=22x-1Γ(x)2 /Γ(2x)
を得る。Γ(1/2)=π1/2より
Γ(2x)=22x-1π-1/2Γ(x)Γ(x+1/2)
が成り立つことが示された。
Γ(n)=(n-1)! 、Γ(1/2)=π-1/2なので、x=4のとき
Γ(8)=22*4-1π-1/2Γ(4)Γ(4+1/2)=23Γ(4)・24Γ(4+1/2)π-1/2
24Γ(4+1/2)π-1/2=24・7/2 Γ(7/2)π-1/2=24・7/2・5/2・3/2・1/2 Γ(1/2)π-1/2
=7・5・3・1
23Γ(4)=23(3・2・1)=6・4・2
Γ(8)=7!=7・5・3・1・6・4・2
を表しています。
<ガンマ関数の相反公式>
Γ(x)Γ(1-x)=π/sin(πx)
を証明します。その前にこの公式の直感的な説明をします。
Γ(x)はx=0,-1,-2,・・・でのみ1位の極をもちます。Γ(1-x)はx=1,2,3,・・・でのみ1位の極をもちます。
f(x)=1/Γ(x)Γ(1-x)は全ての整数で1位の零点をもちます。xをx+1にすると
Γ(x+1)Γ(1-(x+1))=xΓ(x)Γ(-x)=-xΓ(x)Γ(1-x)
ので、f(x+2)=-f(x+1)=f(x) となり、f(x)は周期2の関数であることが分かります。x=1/2で最大値
f(1/2)=1/Γ(1/2)Γ(1-1/2)=1/π
をとります。よってf(x)=sin(πx)/πと予想できます。
証明に入ります。先ほどもとめたベータ関数の性質は
(4):B(x,1-x)=∫[0,∞] ux-1/(1+u) du
(5):B(x,1-x)=Γ(x)Γ(1-x)
ですから、
∫[0,∞] xa-1/(1+x) dx=π/sin(πa) 0<a<1
を示せばよいことが分かります。
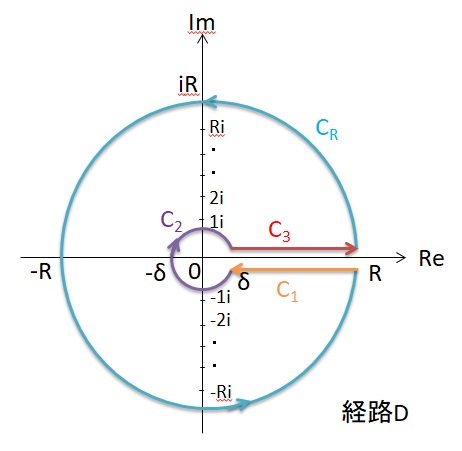
D積分閉路を使って
f(z)=za-1/(1+z)
の複素積分を行います。D積分閉路は
D=C1+C2(ε)+C3+CR
からなります。
ε→0、R→∞で
∫C2(ε)f(z)dz→0、∫CR f(z)dz→0
となります。0<a<1より、-1<a-1<0、に注意すると
-ε+1≦εeiθ+1≦ε+1より、1/|(εeiθ+1)|≦1/(1-ε)
なので、z=εeiθ、dz=iεeiθdθ、0<a<1、より
|∫C2(ε)f(z)dz|≦∫[0、2π]|(εeiθ) a-1|/|εeiθ+1||iεeiθ|dθ
≦εεa-1/(1-ε) 2π=2πεa/(1-ε) → 0 as ε→0
同様に、-1<a-1<0、より
|∫CRf(z)dz|≦∫[0、2π]|(Reiθ) a-1|/|Reiθ+1||iReiθ|dθ
≦2πR・Ra-1/R=2πRa-1 → 0 as R→∞
となります。
z a-1はz=0で特異点を持ちますが、z=0は経路D内には含まれません。
D積分閉路内の極は、z=-1だけです。f(z)のz=-1での留数は
Res[f,-1]=lim[x→-1] (z+1) z a-1/(z+1)=(eiπ) a-1=eiπa e-iπ=-eiπa
∫D f(z)dz=2πi Res[f,-1]=2πi (-eiπa)
となります。
C3上での偏角は0だからz=xe0代入して、ε→0、R→∞で
∫C3 f(z)dz=∫[ε、R] xa-1/(1+x) dx → I=∫[0、∞] xa-1/(1+x) dx
C1上での偏角は2πなので、z=xe2πi代入して、ε→0、R→∞で
za-1=(xe2πi) a-1=x a-1e2πiae-2πi=x a-1e2πia
∫C1 f(z)dz=∫[R、ε] e2πia xa-1/(1+x) dx →∫[0、∞] xa-1/(1+x) dx
となります。従って
2πi (-eiπa)=I+0+I+0=(1-e2πia)I
これをIについて解くと
I=2πi (-eiπa)/ (1-e2πia)=2πi (-eiπa)/(-eiπa) (eiπa-e-iπa)
=π/sin(πa)
が得られます。