現代情報社会に欠かせなくなった暗号には素数の性質が使われています。素数は1と自分自身以外で割り切れない数のことです。具体的には
- 素数={2,3、5、7、11,13,17、19、23、・・・}
なる自然数です。素数には1を含めません。そうすると全ての数は素数の積として一意に表すことができます。いわば素数は自然界の原子のような存在です。しかし素数は無限にあります。
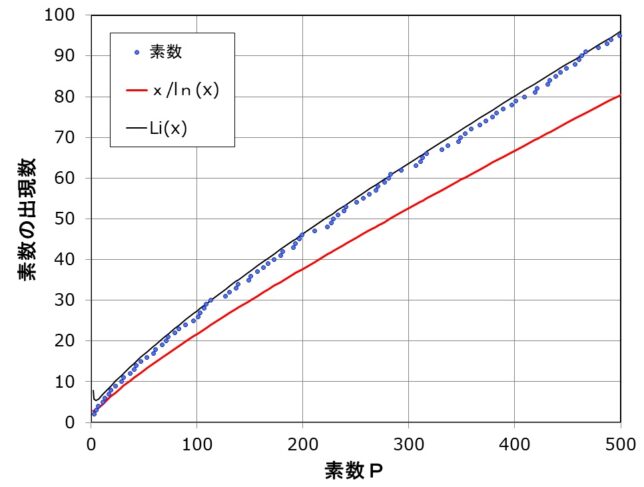
自然数n以下の素数の個数をπ(n)と表します。図1にy=π(x)のグラフを示します。例えば50番目の素数229と95番目の素数499はそれぞれ(229,50)と(499,95)にプロットされています。500以下には95個の素数があるので、π(500)=95です。
驚くべきことに、素数の出現の仕方には規則性がないのに、素数はほぼ一つの曲線の近傍に分布しているように見えますが、その理由は今でも良く分かっていません。お子さんに素数の分布曲線を見せることで、未知の法則に対する興味関心を引き出すことができるでしょう。
素数を見出す確率はどのくらいでしょうか。1792年にドイツの数学者ガウス(当時15歳)は、数nの近傍で素数を見出す確率は1/log(n)と予想しました。その場合に自然数n以下の素数の個数は
- Li(n)=∫[2→n] 1/log(t) dt
と表せます。ここでlogは自然対数です。展開近似すると
- Li(n)≒n/log(n)+n/(log(n))^2 → n/log(n) as n→∞
となります。n→∞の極限で両者が一致するという意味で
- Li(n)~n/log(n)
と書き表します。実際に
- π(n)~Li(n)
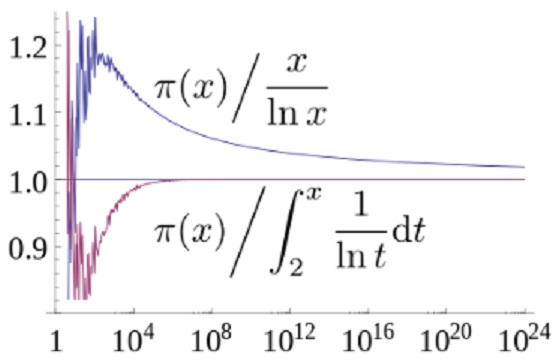
となっています。xが大きい数のとき、xまでの数の中に素数を見出す確率π(x)/xは、1/log(x)、すなわち
- π(x)~f(x)=x/log(x)
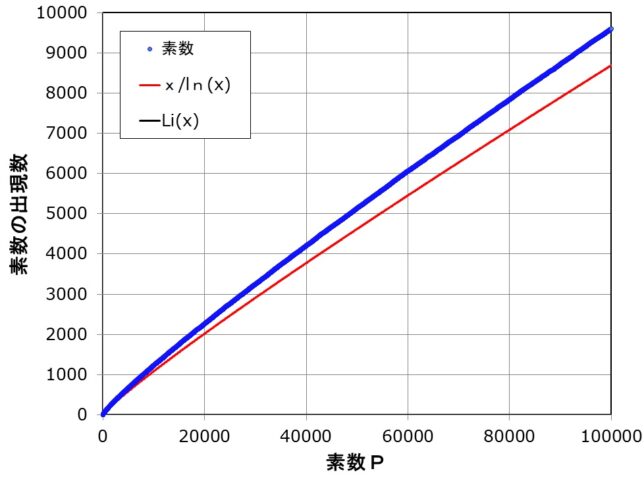
と考えられます。図2に10万までの素数の分布曲線を示します。10万程度ではx/log(x)の近似は誤差が大きいことが分かります。
この定理を使うと、例えば100億までに約4.5億個の素数があることがすぐに計算できます。
x=10nのとき、
- f(10n)=10n/log(10n)=log(e)/n・ 10n≒log(27/10)/n・ 10n
=(3log3-1) /n・ 10n≒(0.434/n)×10n
x=100億=1010の時、素数の数は
- f(1010)≒434/10・ 1010=4.34億個
と予想されます。実際、100億より小さい素数の数は
- π(1010 )=455,052,511=4.55億個
なので、4.6%の誤差で当たっています。Li(x)の場合、
- Li(1010) ≒ 455,055,615
なので、0.0007%の誤差しかありません。