p、qが小さい素数の場合に、公開鍵と秘密鍵を求めてみましょう。

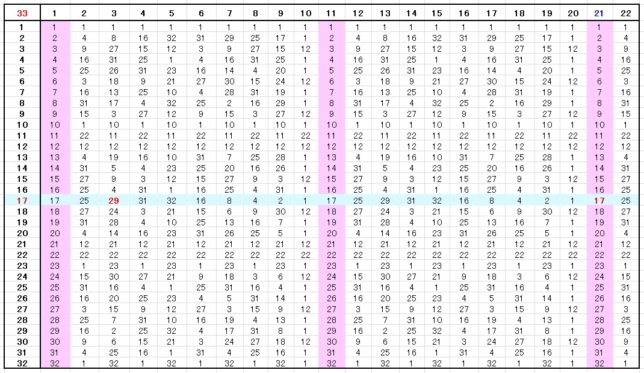
（2）N=33（p＝3、q＝11）の場合
　N＝p×q＝3×11と因数分解できる場合を考えます。(p－1) (q－1)＝2×10＝20です。N＝33を法とする場合、剰余値には0~32までの33個の数しか現れません。表2にべき乗の法を33とした値を示します。2と10の最小公倍数（LCM）は10ですから、
・ 　n・LCM＋1＝11、21、31、41、51、61、・・・（ｎ＝1.2.3.・・・）
となります。21＝3×7、51＝3×17、91＝7×13、111＝3×37ですが、鍵の候補は、20以下の自然数なので、
・ （公開鍵、秘密鍵）＝（3、7）、（3、17）、（7、13）
となります。公開鍵と秘密鍵を入れ替えても構いません。例えば、平文値が17の場合、公開鍵3を用いて17を法33の下で3乗して暗号値29を得ます。復号時には、秘密鍵7を用いて、29を法33の下で7乗すると元の値17に戻ります。3乗して7乗するので、平文値ｍが21乗され、元の値ｍに戻ります。

表2　べき乗の法を33とした値

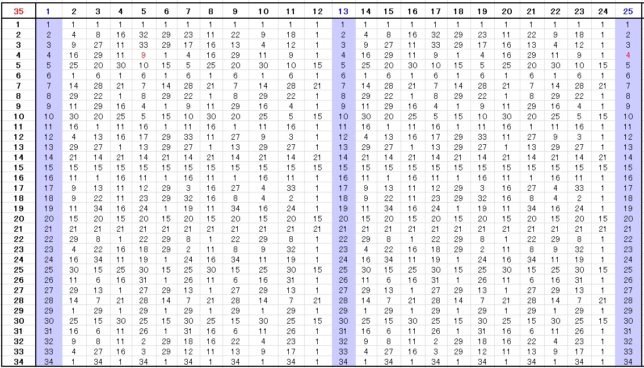
（3）N=35（p＝5、q＝7）の場合
N＝p×q＝5×7と因数分解できる場合を考えます。(p－1) (q－1)＝4×6＝24です。N＝35を法とする場合、剰余値には0~34までの35個の数しか現れません。表3にべき乗の法を35とした値を示します。4と6の最小公倍数（LCM）は12ですから、表3の暗号値は周期12で変化していることが分かります。
・ 　n・LCM＋1＝13、25、37、49、61、73、85、97・・・（ｎ＝1.2.3.・・・）
となります。鍵の候補は、24未満の自然数なので
・ （公開鍵、秘密鍵）＝（5、5）、（7、7）、（5、17）（11、11）（7、19）
となります。公開鍵と秘密鍵を入れ替えても構いません。

表3　べき乗の法を35とした値

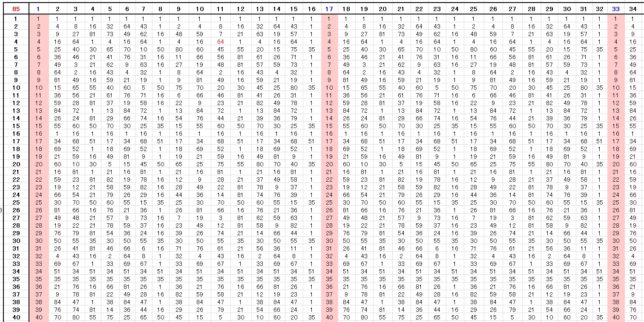
（4）N=85 （p＝5、q＝17）の場合
N＝p×q＝5×17と因数分解できる場合を考えます。(p－1) (q－1)＝4×16＝64です。N＝85を法とする場合、剰余値には0~84までの85個の数しか現れません。表4にべき乗の法を85とした値を示します。4と16の最小公倍数（LCM）は16ですから、表4の暗号値は周期16で変化していることが分かります。
・ 　n・LCM＋1＝17、33、49、65、81、97、113、129・・・

となります。鍵の候補は、64未満の自然数なので
・ （公開鍵、秘密鍵）＝（3、11）、（7、7）、（5、13）、（3、43）、（5、29）、（7、23）、（3,59）
となります。公開鍵と秘密鍵を入れ替えても構いません。実際の暗号にはもっと大きな数が用いられます。

表4　べき乗の法を85とした値

（5）N＝20190707（p＝4567、q＝4421）の場合
2019年の七夕の日にちなみ20190707という比較的大きい数字を考えましょう。
・ N=20190707＝4567×4421
と素因数分解できます。つまりN＝20190707、p＝4567、q＝4421です。
・ （ｐ－1）（q－1）＝4566×4420＝20181720

　　（＝2 * 2 * 2 * 3 * 5 * 13 * 17 * 761）
を法（mod）とする剰余計算を行います。剰余計算とは、法で割った余りを与える計算です。
法(p－1)(q－1)と互いに素な自然数C（公開鍵）に対して、
・ C×D≡1　mod (p－1)(q－1)　かつ　0≦D≦(p－1)(q－1)
を満たす数D（秘密鍵）が存在します。例えばC＝707（＝101×7）に対して、
・ 707×D≡1　mod 20181720　かつ　0≦D≦20181720
なる自然数Dは997525043です。なぜなら
・ 707×997525043＝705250205401
・ 20181720×34945＝705250205400
より
・ 707×997525043＝20181720×34945＋1
が成り立っているからです。受信者は、（N、C）＝（20190707、707）を公開し、D＝997525043は秘密鍵として非公開にします。送信者は、送りたいメッセ－ジを数字ｍ（0≦ｍ≦N）に変換し、公開鍵Cを用いて
・ K＝ｍ^C mod N
なる暗号文Kを送信します。暗号文Kは公開鍵から復号することはできません。受信者は、秘密鍵Dを用いて暗号文Kを復号し
・ ｍ＝K^D mod N
元のメッセ－ジｍを得ることができます。代入すると
・ （ｍ^C mod N）^D mod N＝ｍ^CD mod N＝ｍ　・・・（3）
となります。最後の等式（3）は、次に示すオイラ－の定理より、
・ CD≡1 mod (p－1)(q－1) かつ　0≦D≦(p－1)(q－1)
を満たす秘密鍵Dであれば、成り立ちます。Nを因数分解し、pとqを得られれば、(p－1)(q－1)を法として、公開鍵Cに対する秘密鍵Dを求めることができます。

（6）オイラ－の定理とは
オイラ－の定理とは、正整数ｍ、Nに対して、ｍ、Nが互いに素であるとき、
・ ｍ^φ(N)≡1 mod N　・・・（4）
が成り立つというものです。ここでオイラー関数φ(N) は「Nより小さい正の整数のうち、Nと互いに素な数の個数」を表す関数です。素数Pの場合φ(P)＝P－1となります。
・ φ(N)＝φ(pq)＝(p－1)(q－1)
となります。（2）式をｖ乗して、両辺にｍをかけると
・ ｍ^（φ(N)v+1）≡ｍ mod N　・・・（5）
（3）と（5）を比較すると
・ CD＝φ(N)v+1
を満たす整数Dとｖが存在しれば、復号できることが分かります。一次不定方程式の整数解の定理により、Cとφ(N)が互いに素であれば、整数Dとｖが存在します。もしDが負なら、
・ C（D＋ｋφ(N)）－φ(N)（v＋ｋC）＝1
と変形し、十分大きい数ｋを用いて、Dを正数D＋ｋφ(N)に置き換えることができます。

近年、ビットコインなどの暗号通貨が登場してきました。こうしたものはRSA暗号や楕円曲線暗号などの暗号技術に支えらえています。RSA暗号とは、ロナルド・リベスト、アディ・シャミア、レオナルド・エーデルマンの3人の暗号研究者が1978年に発明した公開鍵暗号の一つです。これは桁数が大きい合成数Nをp×qと素因数分解するのが困難であることを利用した暗号です。p、qが小さい素数の場合に、公開鍵と秘密鍵を求めてみましょう。

・暗号とは
　メッセ－ジは文章で書かれていますが、文字と空白を数字に対応させることで、メッセ－ジ（平文）を一つの大きな自然数ｍに対応づけることができます。公開鍵暗号とは、第三者が読めないように、公開鍵を用いて数ｍを別の数値Mに変換して送信する技術です。受信者は、秘密鍵を用いて暗号文Mを元の平文値ｍに復号します。公開鍵暗号では、公開鍵から秘密鍵を推定できないように工夫されています。

・剰余とは
暗号化には平文ｍより大きな数を法とする剰余計算を用います。剰余計算とは、ある数（法）で割った余り（modulo）を与える計算です。例えば法13における50の剰余は、50を13で割った余り11となります。これを
・ 50 mod13＝（3×13+11）mod13＝11
と表記します。剰余計算により、暗号文Mが法より大きくなるのを防ぎます。
剰余計算には
・ A×B mod C＝（A mod C）×（A mod C）mod C
といった性質があります。例えば、A=50、B=41、C=13の場合
・ 　　41 mod 13=（3×13+2）mod13＝2
ですから、
・ 50×41 mod13＝(50 mod13)×(41 mod13)＝11×2 mod13＝(13+9) mod13＝9
となります。こうした規則を用いると、計算量を減らすことができます。

・オイラ－数φ(N)とは
Nより小さい正の整数のうち、Nと互いに素な自然数の個数をオイラ－数φ(N)と言います。N=10の場合、10より小さく、10と互いに素な数は、｛1、3、5、7｝の4つなので、φ(10)＝4となります。素数pの場合、pより小さく、pと互いに素な数は｛1、3、5、・・・p－1｝のp－1個なので、φ(p)＝p－1となります。pと異なる素数qを用いて、N＝pqと素因数分解できる場合は、｛1、3、5、・・・p－1｝×｛1、3、5、・・・q－1｝によって生ずる(p－1) (q－1)個の数はいずれもNと互いに素であるので、φ(N)＝(p－1) (q－1)となります。
正整数ｍ、Nに対して、ｍ、Nが互いに素であるとき、
・ ｍ^φ(N)≡1 mod N　・・・（1）
が成り立ちます。これをオイラ－の定理といいます。ここでｍ^3＝ｍ・ｍ・ｍの意味です。N＝pqの時は、Nに素な数ｍに対して
・ 　　ｍ^(p－1) (q－1)≡1 mod pq　・・・（2）
が成り立ちます。法pqの下では、平文ｍの指数を増やしていくと、(p－1) (q－1)乗で元に戻る周期的な性質があることを示しています。RSA暗号はこの性質を用いて、作られています。

（1）N=21（p＝3、q＝7）の場合
　N＝p×q＝3×７と因数分解できる場合を考えます。(p－1) (q－1)＝2×6＝12です。Nを法とする場合、剰余値には0~20までの21個の数しか現れません。表1にべき乗の21を法とした値を示します。

表1  べき乗の21を法とした値

これは左端のある数ｍ（1≦ｍ≦20）に対して、1乗、2乗、3乗、・・・26乗した値に対して法21をとった結果を表にしたものです。法21の下では、7乗、13乗、19乗、25乗すると、1~20の値が元の値に戻ることが分かります。この表から、指数が6増加すると周期的に同じ値を繰り返すことが分かります。つまり（2）式
・ ｍ^6 mod21≡1
が成り立っていることを示しています。周期6は、(p－1)と (q－1)の最小公倍数（LCM）になっています。平文値ｍがべき乗で同じ値になるのは、指数がn・LCM＋1乗（n=1,2,3,,,）になるときです。つまり、7、13、19、25、31、37、・・・乗の場合です。25は5×5と表せるので、公開鍵を5、秘密鍵を5にすればよいことが分かります。つまり平文値ｍを公開鍵で5乗して暗号化し、秘密鍵で5乗すれば復号できます。秘密鍵d＝5は、（2）式
・ 5×d mod 6 ≡ 1
を満たしています。なぜなら、
・ 25 mod 6 ＝(6×4＋1) mod 6 ≡1
だからです。表1で、例えば平文値が4の場合、4を5乗すると、暗号値は16になります。さらに5乗すると暗号値16は元の平文値4に復号されます。ｍがどんな値であっても
・ （ｍ＾5）^5 mod 21＝ｍ^25 mod 21≡(ｍ^6)^4・m mod 21≡ｍ
が成り立つので、ｍは25乗すると元に戻ります。