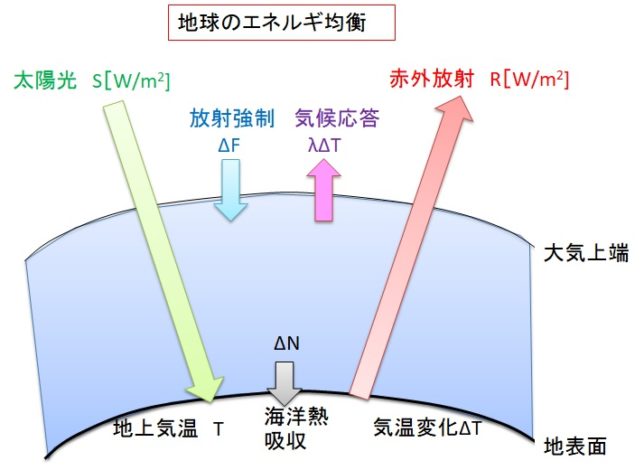
IPCC第4次評価報告書によれば、放射強制力は、対流圏での循環バランスが取れた状態を初期状態とし、これに何らかの原因によってずれが生じたとき、成層圏の気温の変化を考慮したうえで、再び対流圏での循環バランスが取れるようになるまでに変わる放射の量として定義されています。CO2濃度変化が大きいほど放射強制力Fは増大します。
放射強制力は、フロンのような微量ガスの濃度増加に対しては線形に変化します。CO2ガスに対しては濃度増加比の対数に比例して変化すると考えられています。IPCC (1990)およびMyhre (1998)らは、
- ΔF = 5.35 × ln ( C/C0 )
の式を持ちいています。例えば、地球大気中の二酸化炭素の平均濃度が300ppmから400ppmに上昇した場合CO2の放射強制力ΔFは
- Δ F = 5.35 × ln ( C/C0 ) = 5.35 × ln (400ppm /300ppm) = 1.54[W/m2]
となります。産業革命時のCO2濃度285ppmを基準にすると、2100年直前にCO2濃度が2倍になると予測されています。この場合、CO2の放射強制力は
- ΔF=5.35・ln(570ppm/285ppm)=5.35・ln(2)=3.7[W/m2]
となります。このとき
- ΔT=F/λ=3.7[W/m2]/ 1.25[W/m2K] =2.96≒3K
つまり地表気温の上昇は約3Kと推定されています。
IPCC(気候変動に関する政府間パネル)委員会はCO2濃度変化の異なる4つのシナリオを検討しました。それらはRCP2.6、RCP4.5、RCP6.0、RCP8.5と呼ばれています。これは2100年におけるCO2の放射強制力Fが、
- F=2.6[W/m2] 低レベル
- F=4.5[W/m2]、6.0[W/m2] 中レベル
- F=8.5[W/m2] 高レベル
の4つの場合に相当しています。
有効射出温度
現在の気候では、観測可能な大気上端での上向き長波放射(OLR=Outgoing Longwave Radiation)の観測値は235W/m2(Kiehl and Trenberth 1997)です。地球を黒体とみなした時の有効射出温度は、ステファンボルツマンの法則
・R(=235)=σT4=5.67×10-8T4
より、T=254K(=-19℃)です。これは、エネルギ平衡モデル
- (1-A)S・πr2=4R・πr2
から求めた温度、
- T4=(1-A)S/4σ、反射率A=0.3、太陽放射S=1365W/m2
T=255K(=-18℃)とほぼ一致しています。これは温室効果ガスがないときの地表面の温度に相当します。気温減率6.5[K/km]なので、-18℃の高度は、地表面温度15℃のとき、
- H=(15+18)[K]/6.5[K/km]=5.2[km]
です。大気上端8kmでの温度は-37℃ですが、地球からの熱放射は-18℃の大気からの黒体放射と考えられます。
1℃あたりの大気上端での放射束の変化は
- λp=dR/dT=4σT3=4・(5.67×10-8)(254K)3=3.72[W/m2K]
となります。これをプランク応答と呼びます。我々の体温を36℃とすると、517[W/m2] の熱放射と6.7[W/m2 K]のプランク応答があります。体温が1℃上がると、6.7[W/m2]の熱が逃げるので、体が冷えます。つまりプランク応答には負のフィ-ドバック効果があります。
水蒸気の応答はプランク応答の70%程度
- λH2O=2.5[W/m2K]
だと言われています。よって気候感度ΔTは
- ΔT=F/λ=F/(λp-λH2O)=3.7[W/m2]/(3.72-2.5)=3.7/1.22=3.0[K]
となります。2100年にCO2の増加により放射強制が3.7[W/m2]となるシナリオでは、数十年かけて3[K]程度の気温上昇があると予測されます。