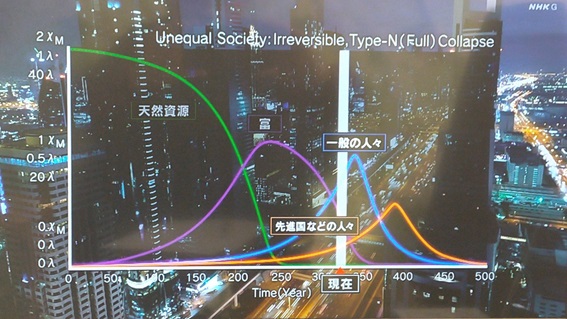
NHKスペシャル・2030 未来への分岐点(1)「暴走する温暖化脱炭素への挑戦」に続いて、2021年2月7日(日)に2030 未来への分岐点 (2)「飽食の悪夢〜水・食料クライシス〜」が放送されました。先進国の飽食が、世界中に「飢餓のパンデミック」を拡大させるという話です。番組では俳優の森七菜さんが2050年の日本で食糧危機に直面する女性を演じました。日本で一年間に出される食品廃棄物を世界に分配すれば、飢餓問題の多くを解決すると言われています。現在の食料システムを2030年までに改善できなければ、暴動が発生し破滅を回避できなくなると研究者たちは指摘しています。
米国メリ-ランド大学の理論環境学者のSafa Mote博士は、2014年に「人間と自然の動力学(=Human And Nature Dynamics)~社会の崩壊か持続における不平等と資源利用のモデル化~」と題して、論文を発表しました(Ecological Economics 101(2014)90-102)。このモデルをHANDYモデルと呼びます。
Safa Mote博士は、自然から収奪する富の蓄積と富の再分配をモデル化して、平等社会と不平等社会における人口変動を予測しました。Safa Mote博士はHANDYモデルにおいて
- 平等社会では、最適な収奪率δ*で富を蓄積すると、収容人口は最大になり、持続可能な社会が実現する。
- 自然からの収奪率が大きくても小さくても、自然環境が収容できる人口は減少する。
- 不平等社会では、持続可能な文明社会が実現できない。
ことを示しました。ここでは、HANDYモデルの詳細について解説します。
- Handyモデルとは
Safa Mote博士が2014年に提案した「人間と自然の動力学(Handyモデル」」は、一般の人口Xc、エリ-トの人口XE、自然資源量y、富の総量wの4つの量の時間発展を4つの連立微分方程式で表したモデルです。その名の通り、このモデルは文明存続を議論するための最もお手軽なモデルになっています。
(1)一般人の人口Xc
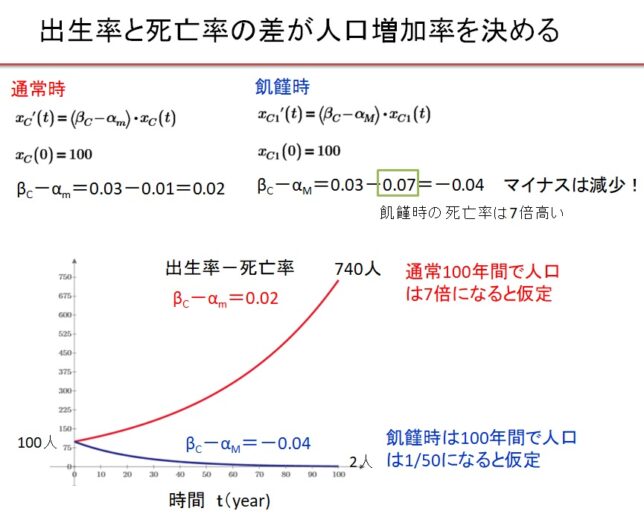
人口増加は、出生率をβ、死亡率をαとすると
- dXc/dt=(β-αc)Xc
と表されます。ここで
αc=αc(Xc、XE、w)、β=出生率定数
です。α、βがともに定数の場合、一般人の人口変動は
- Xc(t)=Xc (0)・exp{(β-α)t}
と書き表されます。出生率が死亡率より大きい場合(β-α>0)、一般の人口Xcは指数関数的に増加します。逆に出生率が死亡率より小さい場合(β-α<0)、一般の人口Xcは指数関数的に減少します。
(2)エリ-トの人口XE
エリ-トの人口も同様に微分方程式
- dXE/dt=(β-αE)XE
αE=αE(Xc、XE、w)、β=出生率定数
と表されると仮定します。
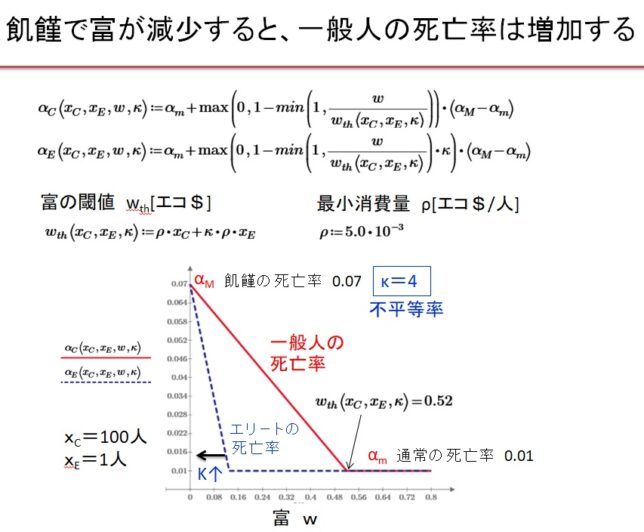
一般に死亡率をαは、人口や富の量に依存します。富の量が人口を養うのに十分であれば、一定になりますが、富の量が閾値wthより小さくなると、死亡率は増大します。一般人とエリ-トでは死亡率αの富の総量wに対する依存性が異なります。
(3)富の閾値wthと不平等率kと死亡率αの富w依存性
ρ[$/人]を一般人一人当たりの最小消費量とすると、富の閾値は
・wth(Xc、XE、k)=ρ・Xc+k・ρ・XE
と表されると仮定します。ここで因子kは不平等率です。エリ-トの最小消費量は一般人のk倍と仮定されています。kの値によって社会を3つに分類できます。
1)平等社会 Egalitarian society k=0、エリ-トなし
2)階級社会 Equitable society k=1、不労所得階級あり
3)不平等社会 Unequal society k>1、エリ-トあり
具体的に、このモデルでは通常の死亡率はαm=0.01、飢饉時の死亡率はαM=0.07としています。死亡率αは、富が閾値を下回ると0.01から0.07に富に比例して増大すると仮定します。一般人とエリ-トでは富の閾値が異なります。エリ-トの富の閾値は小さいので、エリ-トの死亡率は殆ど最小値0.01に固定されています。つまり富の総量wが閾値より減少すると、一般人の死亡率は減少し始めますが、エリ-トの死亡率は低いまま保たれます。
(4)資源量y
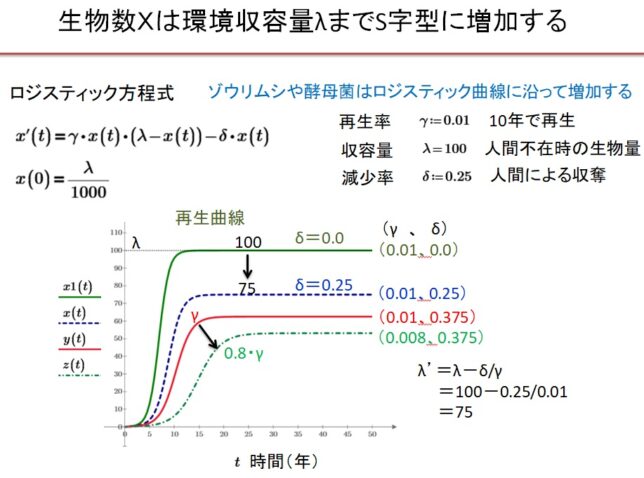
限られた食物環境にある生物の増殖を議論するのには、ロジスティック方程式が用いられます。資源量yは、ロジスティック方程式
・dy/dt=γy(λ-y)-δ・Xc・y
に従うと仮定します。ここでλは人間の収奪がないときの最大資源量です。λの単位は$(エコドル)です。γ[1/t$]は単位時間の自然の再生率です。γ=0.01のとき10年で再生します。δ[1/t人]は一人当たりの人間が1年間に自然から収奪する収奪率です。収奪率δがゼロだと富が蓄積されません。仮にy(0)=λ/1000とすると、δ=0のときは、資源量y(t)は、S字型の再生曲線を描いて増加し、最大資源量λで飽和します。なぜならλ≫yのときは、指数関数的に増大し、yが増大してλに接近するとyは一定値λになるからです。
δがゼロでないときは
・dy/dt=γy(λ-δXc/γ-y)=γy(λ’-y)
と書けます。資源量y(t)は、S字型の再生曲線を描いて増加しλ’で飽和します。
λ=100、γ=0.01、δ=0.0025、Xc=100のときは
・λ’=λ-δXc/γ=100-0.0025*100/0.01=100-25=75 <100=λ
となります。
y<<1の時は、yの2次の項を無視して
・dy/dt=(γλ-δXc)y
と近似できます。収奪率δがγλ/Xcより大きくなると、資源量yは減少し、人類は滅んでしまうことが分かります。収奪率δが
・δ[1/t人]=γ[1/t$]・λ[$]/Xc[人]=0.01・100/100=0.01
のとき、資源量yは一定になります。
(5)富の総量w
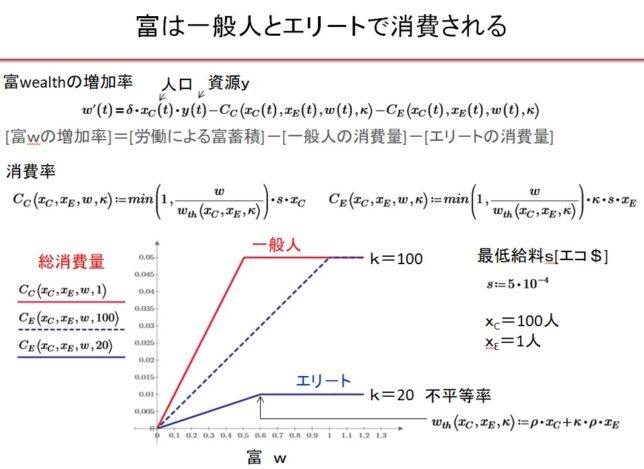
富の総量wは、
・dw/dt=δXc・y-Cc(Xc、XE、w、k)-CE(Xc、XE、w、k)
に従うと仮定します。1年間の富の増加量は、自然から得た収奪量から一般人による富の消費量Cc[$/t]とエリ-トによる富の消費量CE[$/t]を引いた値になります。自然からの収奪量と富の消費量が一致する循環社会では、富は一定の値に保たれ、人口も安定します。
最低給料をs[$/人]とすると、一般人とエリ-トの富の消費量は
・Cc(Xc、XE、w、k)=min(1,w/wth)・s・Xc
・CE(Xc、XE、w、k)=min(1,w/wth)・s・k・XE
と表されると仮定します。エリ-トの消費量の場合は不平等率kがかかります。
ここで富の閾値は
・wth(Xc、XE、k)=ρ・Xc+k・ρ・XE
でした。w>wthの平時では、Ccは最低消費量
・Cc(Xc、XE、w、k)=s・Xc
となり、Ccはwに依存しません。w<wthの飢饉の時は、
・Cc(Xc、XE、w、k)=w/wth・s・Xc
となり、Ccはwに比例します。富の総量wがwthより小さくなる飢餓状況では、人の消費量はwが減るにつれて減少することになります。不平等率kが大きいほどエリ-トの消費量は大きくなります。
(6)初期状態
簡単のため、初期状態は
・一般人の人口:Xc(0)=100[人]、
・エリ-トの人口:XE(0)=1[人]
・資源量:y(0)=100[$]、
・富の総量:w(0)=0[$]
と仮定しています。
2.平衡状態の人口、資源、富の量 XE=0の場合
ここでは、簡単のためエリ-トがいない平等社会での
・dXc/dt=0,dy/dt=0、dw/dt=0
なる平衡状態(定常状態)の解Xce、ye、weを考えます。以下に平衡解の導出方法を示します。
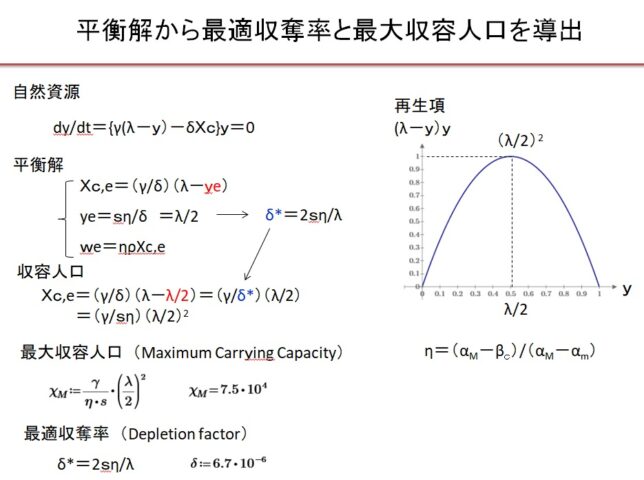
パラメ-タηを
・η=(αM-βc)/(αM-αm)
と定義すると、結局、平衡時の資源量yeは
・ye=sη/δ (=λ/2)
と書けます。平衡時の人口Xce、富weは
・Xce=γ/δ・(λ-ye)
・we=ηρXce
と書けます。平衡時の資源量ye=λ/2のとき、再生項y(λ-y)が最大値λ2/4になるので、このときの収奪率を最適収奪率(Optimal Depletion Ratio)
・δ*=2sη/λ=6.7×10-6
と呼びます。δ=δ*のとき、最大収容量(Maximum Carrying Capacity)
・XM=γ/δ*・(λ-λ/2)=γ/ sη(λ/2)2=7.5×104
が得られます。
3.計算に用いたパラメ-タ
4.Equitable社会の持続可能性の収奪率依存性について
少数の不労者はいるが、不労者の消費量は一般人と同じ(k=1)である階級社会をEquitable societyと言います。kは不平等率です。
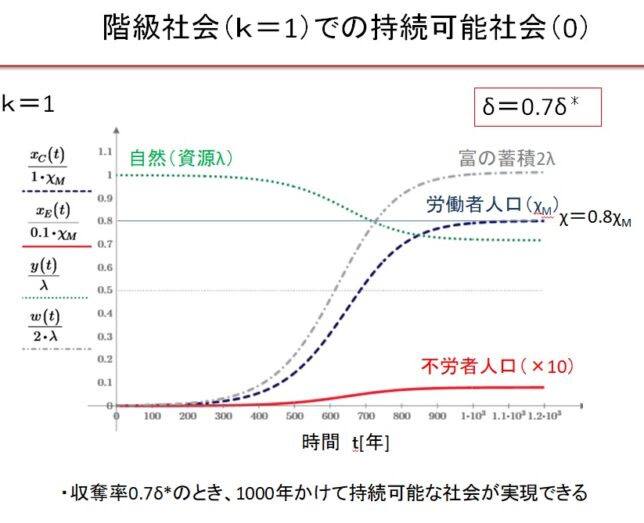
(1)k=1の階級社会 δ=0.7・δ*の場合
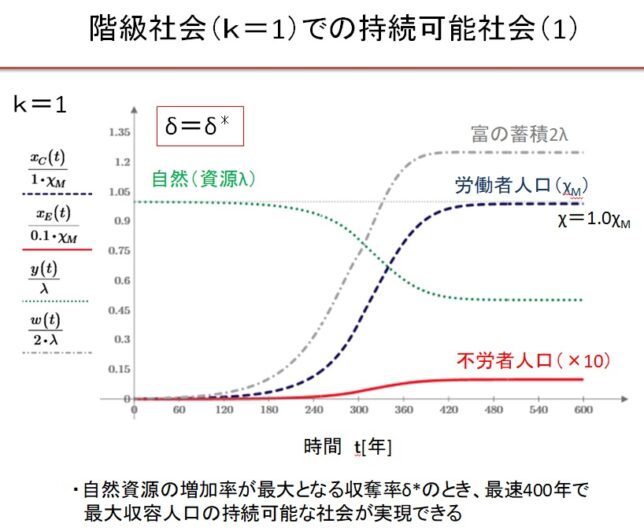
(2)k=1の階級社会 δ=1.0・δ*の場合
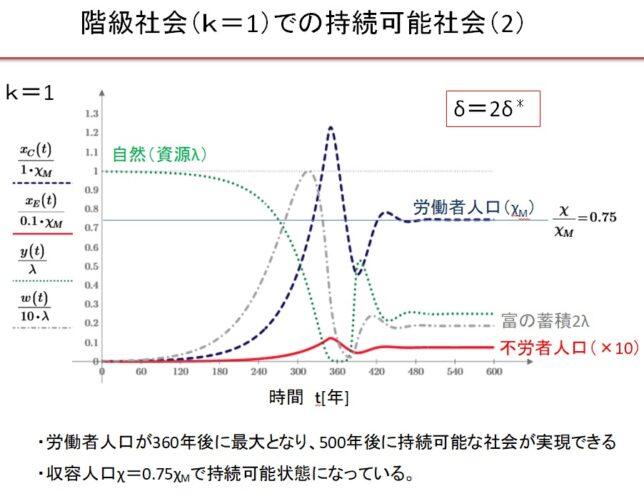
(3)k=1の階級社会 δ=2.0・δ*の場合
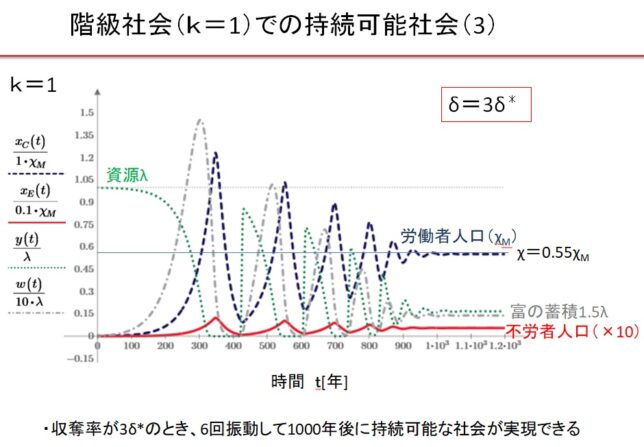
(4)k=1の階級社会 δ=3.0・δ*の場合
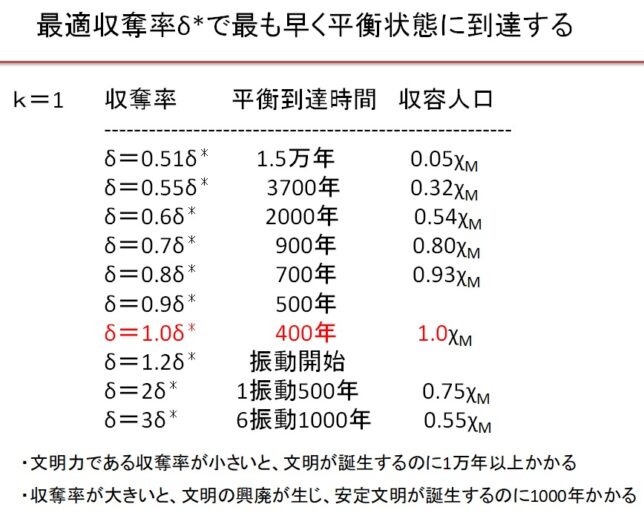
(5)Equitable 社会のまとめ
Equitable 社会では、0.55δ*~3δ*の広い収奪率で持続可能な文明が実現します。収奪率が最適収奪率の0.55倍の場合は、人口増加が遅く、収容人口は最大値の1/3になります。最適収奪率δ*のとき、最速400年で持続可能な社会が実現し、収容人口は最大になります。収奪率が最適収奪率の2倍になると、収容人口は最大値の3/4に減少します。収奪率が最適収奪率の2倍以上になると、振動現象が現れ、持続可能な文明に到達するのに1000年以上を要します。
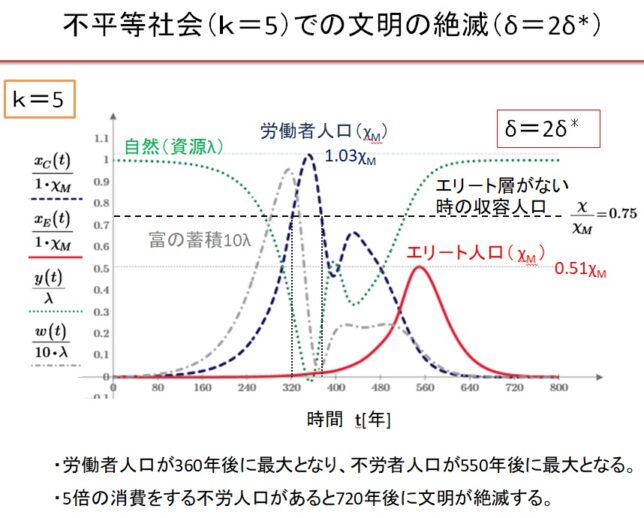
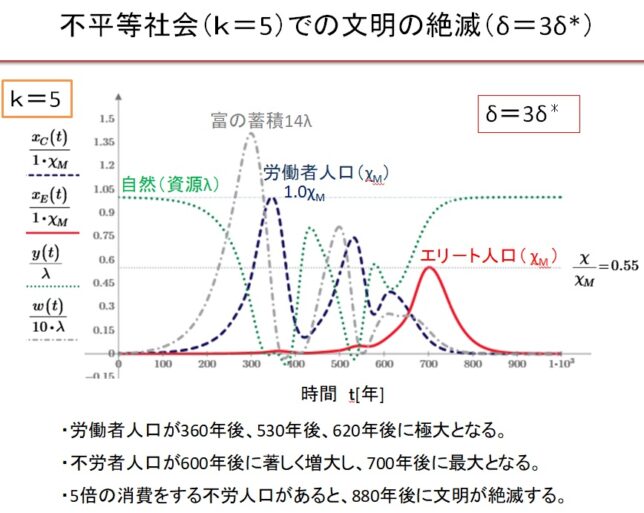
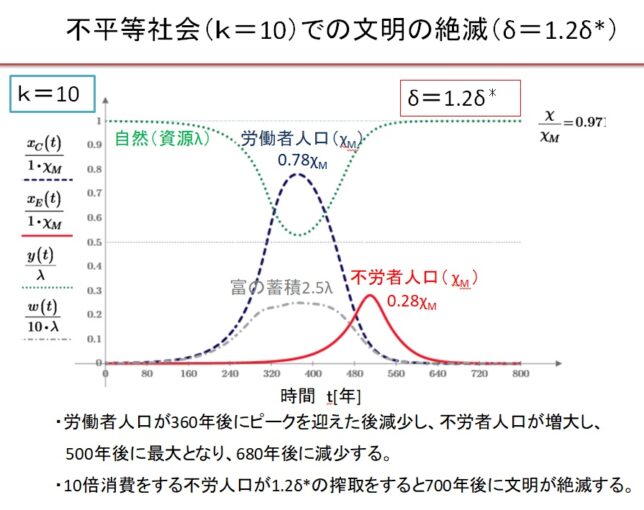
5.不平等社会での文明の絶滅
少数の不労者が一般人の5倍消費している不平等社会では、持続可能な社会が形成されず、文明は崩壊します。
(1)k=5の不平等社会でδ=1.0・δ*の場合
k=5の不平等社会において、Equitable社会で最大人口が達成できる収奪率δ*で収奪すると、文明は崩壊します。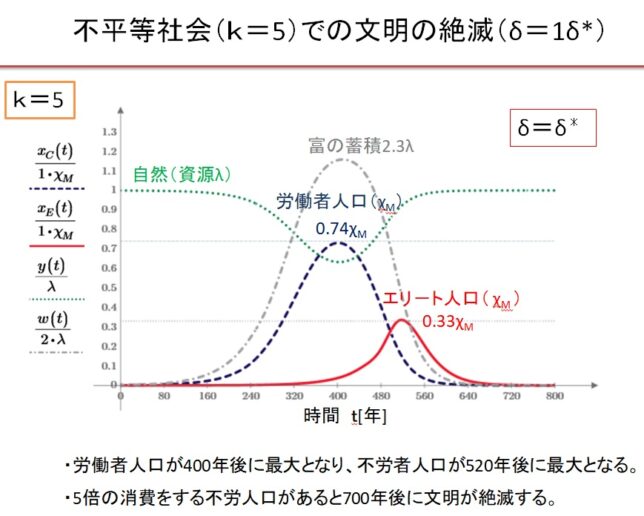
(2)k=5の不平等社会でδ=2.0・δ*の場合
(3)k=5の不平等社会でδ=3.0・δ*の場合
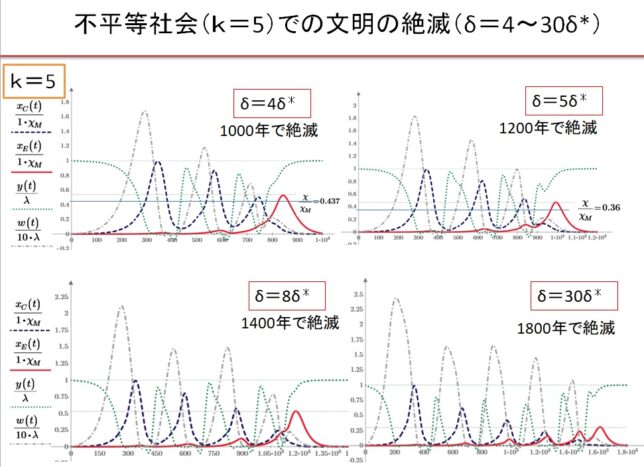
(4)k=5の不平等社会 δ=4~30・δ*の場合
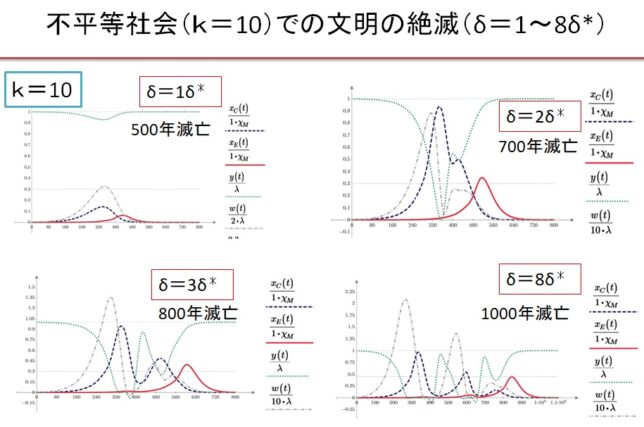
(5)k=10の不平等社会 δ=1~8・δ*の場合
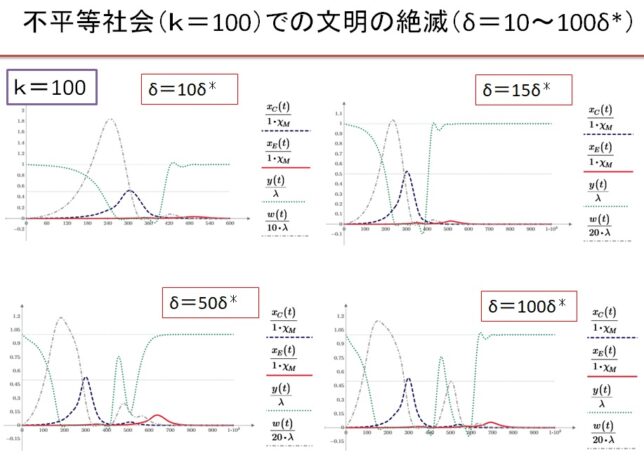
(6)k=100の超不平等社会 δ=10~100・δ*の場合
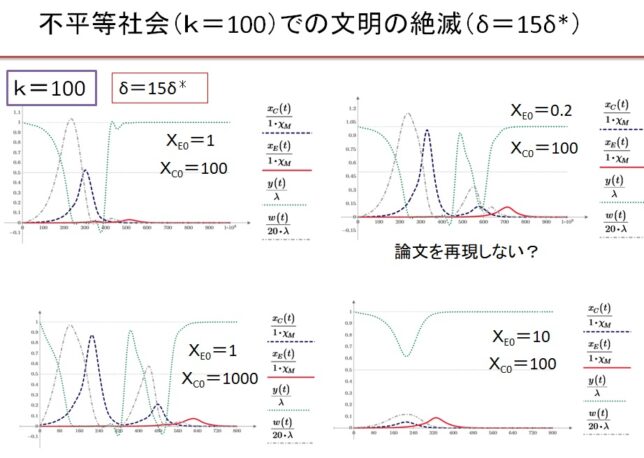
(7)k=100、δ=15・δ*の超不平等社会 初期人口依存性
(9)k=100の超不平等社会 δ=15・δ*の場合
NHKスペシャルで紹介された上記条件の計算結果をほぼ再現した。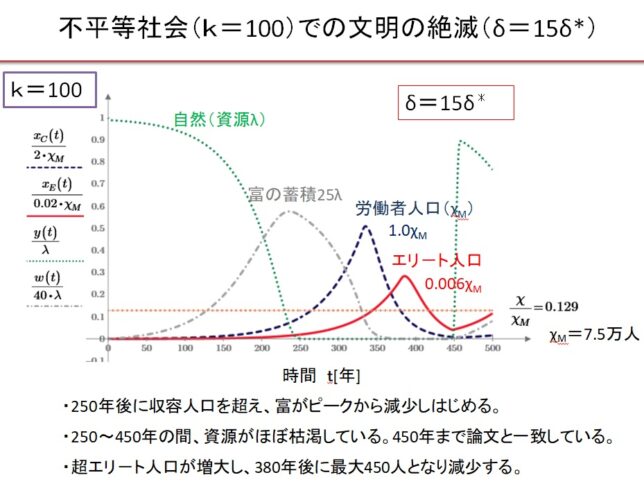
7.モデルの限界
このモデルでは、人口が減少し絶滅しそうになっても、エリ-トの消費量は一般人のk倍を維持していると仮定しています。現実には、人類が絶滅しそうになったら、エリ-トの消費量は一般人と同等になっていくのではないかと思われます。完全に消費量が同等になれば、不平等社会からEquitable社会へ移行し、持続可能な状態が実現します。しかしEquitable社会から不平等社会に逆戻りしたり、不平等が少しでも残れば、文明は絶滅する可能性が高いと思われます。
また文明が継続し技術革新によって死亡率が減少する可能性は考慮されていません。今後の課題としては、そうした修正をいれたモデルの検討が考えられます。
なおこのモデルでは、文明の絶滅原因を資源や富の減少に限定しています。実際は火山の噴火で生き埋めになったり、干ばつで水源が枯渇したり、大規模な洪水や地震などの災害や疫病の蔓延で文明が崩壊する可能性もあります。