大気上端での熱エネルギの収支を考えることで、温暖化のメカニズムを理解できます。

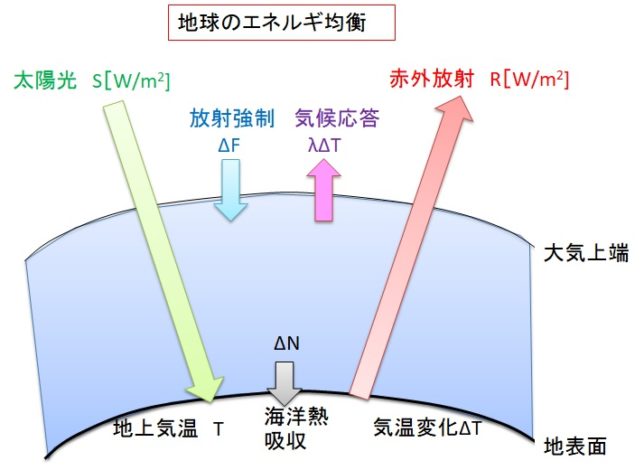
太陽光の照射密度S[W/m²]と赤外線の放射密度R[W/m²]の差をN[W/m²]とします。Nはいわば大気に蓄えられるエネルギ密度です。

• N＝S－R（T、P_CO2、P_H2O、Albedo、Cloud）

ここでTは大気上端の温度、P_CO2はCO2圧力、P_H2Oは水蒸気圧力、Albedoは太陽光の反射率、Cloudは雲量を表し、いずれも温度Tに依存します。赤外放射Rはこれらの諸元の関数になっています。ここで太陽放射Sは1365W/m²で一定であると仮定します。十分時間が経つと、S=Rとなり、大気に蓄えられた出力密度Nはゼロの平衡状態（厳密には定常状態）になります。仮にCO2濃度が急に2倍になると、地表からの赤外放射がCO2によって遮られるので、大気上端での赤外放射Rは小さくなります。このとき

• N＝S－R＞0

となり、大気にエネルギが蓄えられ、気温が上がり、大気上端の温度Tも上昇します。しかし時間が経つと、大気のエネルギNは海洋に拡散していき、やがてN＝0となります。このとき大気上端の温度はΔTだけ上昇した状態でS=Rになると考えられます。

バランス方程式

まず簡単のため、Albedo、Cloudは一定とします。Sは定数なので、CO2濃度がΔP_CO2変化すると、温度がΔT変化するので、大気に

ΔN＝－(∂R/∂P_CO2）ΔP_CO2－(∂R/∂T）ΔT－(∂R/∂P_H2O）(∂P_H2O /∂T）ΔT

のエネルギが蓄積します。ここで

• F＝－(∂R/∂P_CO2）ΔP_CO2＞0
• λp＝∂R/∂T＝4σT³＞0
• λ_H2O＝－(∂R/∂P_H2O）(∂P_H2O /∂T）＞0

と定義します。FはCO2の放射強制力（Radiation Forcing）と呼ばれています。λpはプランク応答、λ_H2Oは水蒸気応答と呼ばれています。ここで応答パラメタλ（フィードバックパラメタ）を

• λ＝λp－λ_H2O＞0

と定義すると、よく知られたバランス方程式

• ΔN＝F－λΔT＞0

が得られます。FはCO2濃度上昇による大気を加熱する効果、λΔTは大気を冷却する効果を表しています。λpは冷却すなわち負の応答効果、λ_H2Oは加熱すなわち正の応答効果を表しています。但し1/λを気候感度パラメ－タと呼ぶ場合もあるので注意が必要です。

一般に応答パラメタλは

• λ＝λp－λ_H2O－λ_Albedo－λ_Cloud＋λ_aerosol ＞0

雲による影響は、計算が難しいですが、太陽光の反射による冷却効果より惑星放射の吸収よる加熱効果の方が高いので正のフィ－ドバック効果があると考えられています。しかしながら応答パラメタλの値は、おおまかにはプランク応答と水蒸気応答の値で決まります。水蒸気の濃度が高いと、応答パラメタλが小さくなるので、気候感度ΔTは増大します。

温度上昇の時間変化

時刻ｔ＝0で、ΔT＝0すなわち、ΔN＝Fです。ｔ＝∞で、ΔN＝0となります。その時間変化の時定数をτとすると、大気に蓄積するエネルギは

• ΔN＝F・exp（－ｔ/τ）

と書けます。バランス方程式に代入すると

• F・exp（－ｔ/τ）＝F－λΔT

これをΔTについて解くと、

• ΔT(t)＝F/λ・[1－exp(－ｔ/τ)]　→　ΔT＝F/λ　（ｔ→∞）

が得られます。これは、十分時間が経ち、バランスを回復した後の温度上昇ΔTがF/λとなることを示しています。ΔTを平衡気候感度あるいは気候感度と呼ばれています。

ちなみに現在の放射平衡の下では、応答パラメタλは

• λ＝1.25[W/m²K]

程度とされています。