ディリクレ積分
∫[0,∞] sin(x) /x dx=π/2
を複素積分
∫C eiz /z dz=0
で求めます。
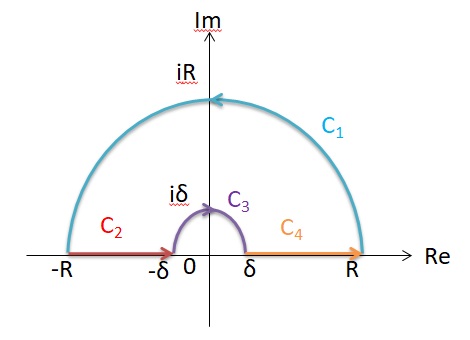
閉積分経路Cを
C=C1+C2+C3+C4
に分けます。ここで
C1:z=Reiθ 0≦θ≦π
C2:z=x –R≦x≦-δ
C3:z=δeiθ 0≦θ≦π
C4:z=x δ≦x≦R
とします。閉積分経路C内にz=0の極は含まれないので、Cでの積分はコーシ-の定理よりゼロになります。
(1)C1の積分
0≦sinθ≦1 かつ 2θ/π≦sinθ(0≦θ≦π)、
ですから、
|exp(iReiθ)|=|exp{iR(cosθ+ i sinθ)}|
=|exp{iRcosθ}・exp{-R sinθ)}]|
=e-R sinθ
≦e-R2θ/π
従って
|∫C1 eiz /z dz|=|∫[0,π] exp(iReiθ) /Reiθ ・iReiθdθ|
≦∫[0,π] e-R2θ/πdθ
=-π/2R・[e-R2θ/π] θ=0,π
=π/2R・(1-e-2R) → 0 as R→∞
C1の積分はRが無限大になるとゼロになります。
(2)C2の積分
ここで x’=‐xに置き換えると
∫C2 eiz /z dz=∫[R,δ] e‐ix’ /x’ dx’=-∫[δ、R] e‐ix’ /x’ dx’
となります。
(3)C3の積分
∫C3 eiz /z dz=∫[π,0] exp(iδeiθ) /δeiθ ・iδeiθdθ
=i∫[π,0] {1+(iδeiθ)+O(δ2)}dθ
→ i∫[π,0] dθ=-iπ as δ→0
(4)C4の積分
∫C3 eiz /z dz=∫[δ、R] eix /x dx
となります。以上より
0=∫C1 eiz /z dz+∫C2 eiz /z dz+∫C3 eiz /z dz+∫C4 eiz /z dz
=∫CR eiz /z dz-∫[δ、R] e‐ix /x dx+∫[δ、R] eix /x dx-iπ
=∫CR eiz /z dz +∫[δ、R] (eix-e‐ix) /x dx-iπ
=∫CR eiz /z dz +2i∫[δ、R] sin(x) /x dx-iπ
ここで δ→0かつR→∞ とすると
2i∫[0、∞] sin(x) /x dx-iπ=0
すなわち
∫[0、∞] sin(x) /x dx=π/2
が得られます。複素積分を用いると簡単にディリクレ積分の値が求められました。