マリアム・ミルザハニ（Maryam Mirzakhani）は双曲面上の測地線に関する優れた研究をした女性のイラン人数学者です。マリアムは1977年5月3日テヘランで生まれました。小さい頃は読書が好きで、将来は小説家になりたいと思っていました。

   1991年、彼女が小学校を卒業するころ、イラン・イラク戦争が終結し、やる気のある学生に対するチャンスが開かれました。彼女は試験を受け、テヘランのファルザネガン中学校に合格しました。そこで生涯の友人となるロヤ・ベヘシュティーに出会います。中学1年生の時は、数学の成績は良くありませんでした。天才は自分の才能に気づいているとは限らないようです。中学2年のときに熱心な先生に出会って、マリアムは数学に自信をもつようになります。

   マリアムはファルザネガン女子高等学校に進学し、ロヤと国内のプログラミング大会に参加します。熱心な校長先生の計らいで、マリアムは1994年（香港）と1995年（トロント）の国際数学オリンピックに出場します。マリアムはそこで金メダルを獲得し、「イランの天才少女」と呼ばれました。数学オリンピックは優れた数学者の登竜門になっています。マリアムはイランのシャリフ工科大で学士号を取得し、ハーバード大学のマクマレン教授の下で幾何学を学び、双曲線幾何学の美しさに魅了され、研究に没頭します。

双曲面上の測地線定理の発見
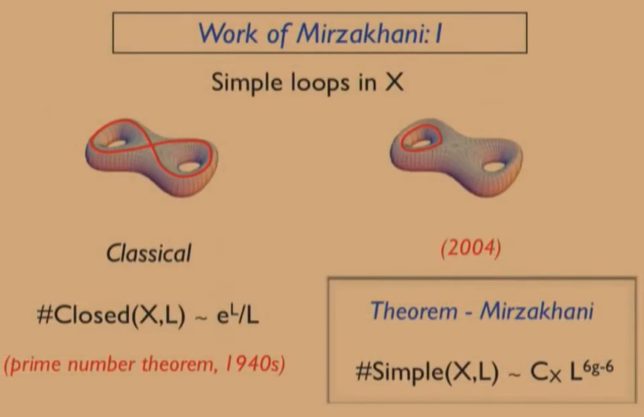
　2004年にマリアムは、双曲面上の測地線に関する重要な定理を発見し、博士学位を取得します。測地線とは2点間の最短距離を結ぶ線のことです。その定理とは、コンパクトな双曲面X上の長さLのシンプルで閉じた測地線の数は、Lの6ｇ-6乗に比例する
　　　＃simple loops＝C(X)・L＾(6ｇ－6)
というものです。ここでｇは双曲面Xの穴（ハンドル）の数です。ド－ナツの場合ｇ＝1、2穴ド－ナツの場合ｇ＝2となります。シンプルな測地線とは自分自身と交わらない測地線のことです。またマリアムは、シンプルで閉じた測地線で切断したときに、双曲面を2分する確率は1/7であることを見出しました。彼女の発見は、弦理論に関連するエドワード・ウィッテンの公式を位相幾何学的に証明する手法を与えました。

オリラ－標数との関係
オイラ－標数とは多面体の位相不変量であり、
     Euler標数＝V（頂点数）－E（辺数）＋F（面数）
で定義されます。例えば三角形の場合、3－3＋1＝1となります。マリアムの公式で気になるのは指数部分6ｇ-6＝－3（2－2g）です。実は2－2gはトーラスのEuler標数です。
       種数ｇのト－ラスのEuler標数＝ 2－2g
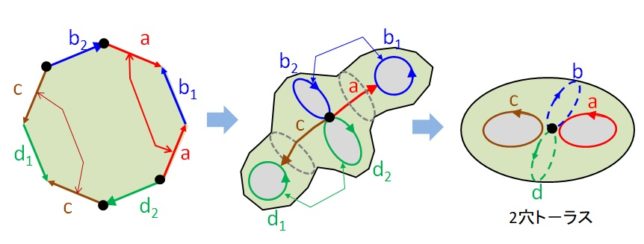
ｇ＝0の多面体面（球面と同相）はEuler標数＝2＞0なので凸面体、ｇ＝1のド－ナツ面はEuler標数＝0なので平坦面、ｇ＝2の2穴トーラス面はEuler標数＝－2＜0なので双曲面となります。2穴ト－ラスのオイラ－標数を求めるには、元の図形の8角形を考えます。8角形を連続的に変形し2穴ト－ラスにすると、頂点は1個に集約され、8辺のうち4個の辺は同一視されたので、辺は4個になり、面は1個のままです。連続的な変形でオイラ－標数は変わらないので、2穴ト－ラスのEuler標数は
　　　Euler標数＝1（頂点）－4（辺）＋1（面）＝－2
と考えられます。

ビリア－ド問題
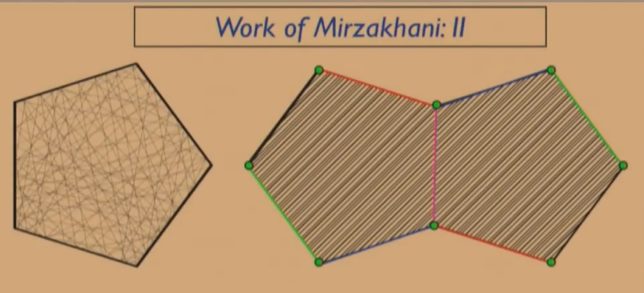
　2006年、ミルザハニは同僚のエスキンとビリア－ド問題に着手しました。ビリア－ド問題とは多角形のビリヤード台の境界で完全反射する光線の通過領域を調べる問題です。例えば5角形内の光線の軌跡を考えます。反射境界において、向こう側へひっくり返された5角形を隣接させると、反射光の軌跡は境界を横切って直進していくように見えます。5角形内の光線の軌跡は多数の隣接した五角形を横切る直線として理解できます。

例えば隣接する2つの五角形は八角形になります。同一視した辺を向きに注意して、図形をゴム膜のように引き延ばしてつなぎ合わせると8角形は2穴トーラスになります。つまりビリア－ド内の光線の軌跡は、多数の穴が開いたト－ラスの測地線となっているのです。任意の角度で放射された光線が元の位置と角度に戻ってくるとしたら、その軌跡はシンプルな閉じた測地線となっているはずです。このようにビリア－ド問題はマリアムが研究していた双曲面上の測地線問題とつながっていたのです。ビリア－ド問題は統計力学のエルゴ－ド問題に関わります。鏡張りの部屋における警備員の視線を解明する問題にも応用されています。

輝かしい経歴と早すぎる死
2008年にマリアムは31歳の若さでスタンフォード大学の教授になりました。夫のヤン・ヴォンドラークはMIT出身のコンピュ－タ理論の研究者です。彼女には三才になる娘アナヒタがいます。2014年にマリアムは37歳のとき女性で初めてフィールズ賞を受賞しました。授賞理由は、リーマン面とそのモジュライ空間の力学と幾何学に関する顕著な業績です。特にウィッテンの公式を証明したことが、高く評価されました。授賞時の様子を見るとマリアムはとても小柄な人だと分かります。
この時マリアムはすでに乳がんを発症していました。残念なことに癌が脊髄に転移し、2017年7月15日にマリアムは40歳という若さで亡くなりました。若くして亡くなったので、一般の人たちは彼女のことを殆ど知りません。

ミルザハニの言葉
ミルザハニの研究は、微分幾何学、複素解析、力学系など数学の多くの分野に影響を与えました。「わたしは、各分野の境界に人が引いた想像上の線を横断するのが好きなのです。研究においては、楽観的であること、異なる物事を結びつけることが重要です」