計測可能な屈折率nを用いて、分極率を表します。単位体積当たりの分子数をNoとすると、分極率αが古典的に

・　α＝（3/No）[(n²－1)/(n²＋2)]

と表せることを説明します。

屈折率ｎの媒質では光速は

・　c＝c₀/n

と小さくなります。よって

・　n²＝(c₀/c)²＝εμ/ε₀μ₀ ≒ ε/ε₀

となります。

外部電場Eo内に設置された誘電体の内部の分子を含む半径roの球を考えます。分子に分極を引き起こす分子にかかる電場Eは

・　E＝Eo＋Ep＋Ei

の3つの成分に分けて考えることができます。ここでEpは半径roの球をくり抜いた外側の誘電体の分極が球の中心につくる電場とします。Eiは球形の分極した誘電体が球の中心につくる電場とします。なお誘電体は等方的で、印加したEoと同じ方向に分極が生じるものとします。分子の位置を原点とし、外部電場の向きをｘ方向とし、ｘ軸からの角度をθとします。

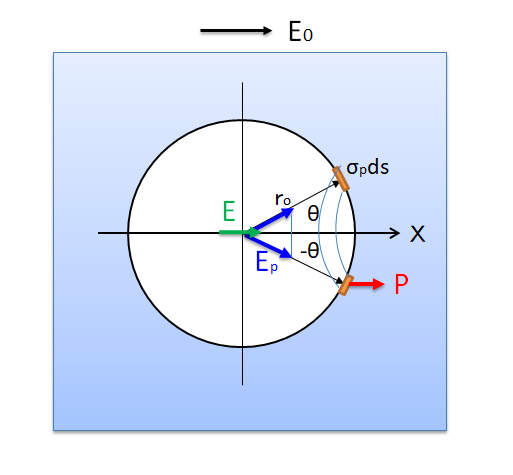
1）Epについて

　外側の誘電体の分極により、半径roの球のｘ＞0の内壁に負の面電荷、ｘ＜0の内壁に正の面電荷が生じています。角度をθの位置にある微小面積dsの電荷密度σpは

・　σp＝∣P∣cosθ

となります。Pは単位体積当たりの双極子モーメントであり、P[Cm/m³]＝P[C/m²]より面電荷と同じ次元をもっています。σpdsの電荷が原点につくる電場のｘ軸方向は

・　dE＝∣P∣cosθds/4πεoro² ・cosθ

角度θとθ+ｄθに挟まれた内壁の帯状の面積は、幅roｄθをもつ半径ro・sinθの円ですから、ds＝2πro・sinθroｄθとなります。内壁の面電荷が原点につくる電場Epは

・　∣Ep∣＝∫_[0、Π] ∣P∣cos²θ/[4πεo・ro²]・2πro²・sinθｄθ

・　　　＝∣P∣/2εo∫_[-1、1] ｔ²dt＝∣P∣/2εo・2/3＝∣P∣/3εo

・　　Ep＝+P/3εo

となります。

2）Eiについて

　原点に微小距離ｄ離れた正負の電荷ｑがあったとします。その点のポテンシャルφを考えると、双極子のエネルギは

・　U＝qφ（ｄ、0、0）－qφ（0、0、0）≒qd＝ｐ(dφ/dx)₀

となります。点rp（xp、yp、zp）にｐ＝qdの双極子があったとき、それが任意の点（x,y,z)につくるポテンシャルφ(x,y,z)は

・　φ(x,y,z)＝(p・r)/4πεoｒ³

　　　　　　＝(1/4πεo)・p（z－zp）/｛（x－xp)²＋（y－yp)²＋（z－zp)²}^3/2

となります。点Pにある双極子の電場により原点にある双極子がもつエネルギは

・　U＝ｐ(dφ/dx)₀＝(p²/r³)（1－3 zp²/r²）

となります。双極子が立方格子状に分布している場合は、格子定数aとすると、整数i、j、kに対して、

・　（xp、yp、zp）＝（ai、aj、ak）

となるので、エネルギは

・　U＝＝p²/a³∑( i²＋j²＋k²) ^-5/2・（i²＋j²＋k²－3ｋ²）

と表せます。和を取る際に（i、j、k）をサイクリックに入れ替えて3で割ると、分母は変わりませんが、

分子＝1/3｛（i²＋j²＋k²－3ｋ²）＋（k²+i²＋j²－3j²）＋（j²＋k²＋i²－3i²）｝＝0

となるので、U＝0となります。したがってEi＝0となります。

したがって、分子に働く電場の強さは

・　E＝Eo＋P/3εo

となります。これをロ－レンツの内部電界といいます。単位体積当たりの双極子数をNo、分子の分極率をαとすると、分極ベクトルPは

・　P＝NoαεoE＝Noαεo(Eo＋P/3εo)

となります。これをPについて解くと

・　P=NoαεoEo/(1－Noα/3)

となります。これを電束密度DにあるPに代入すると

・　D＝εoEo＋P＝εoEo＋NoαεoEo/(1－Noα/3)

　　　＝（1＋2Noα/3）/(1－Noα/3)・εoEo

一方

・　D＝εEo＝（ε/εo）εo Eo

なので

・　ε/εo＝（1＋2Noα/3）/(1－Noα/3)

となります。αについて解くと、双極子の分極率と屈折率の関係式

・　α＝（3/No）（ε/εo－1）/（ε/εo＋2）＝（3/No）（ｎ²－1）/（ｎ²＋2）

が得られます。これをクラジウス・モソッティの式（1879年）といいます。