太陽光の放射強度Iは、大気中を通過する際に散乱されて減衰します。散乱体の密度ρ[kg/m3]と散乱係数σ[m2/kg]を用いると、地表での放射強度をIoとすると、高度zでの放射強度Iは
- I=Io・exp{-∫σρdz}
と表せます。波長λの光のレ-リ-散乱係数σRは、古典電磁気学的には
- σR=32π^3・(n-1)^2/3Noρoλ^4
と表せます(1871年)。ここでNo[個/m3]は空気の分子数、nは空気の屈折率(=1.000292@1atm,0℃)です。
- ρo=1.22[kg/m^3] 標準状態での空気の密度
- No=1.22[kg/m^3]・6.02×10^23[個]/28.964×10^-3[kg]=2.54×10^25[個/m^3]
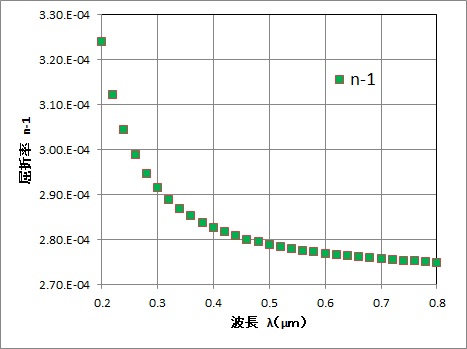
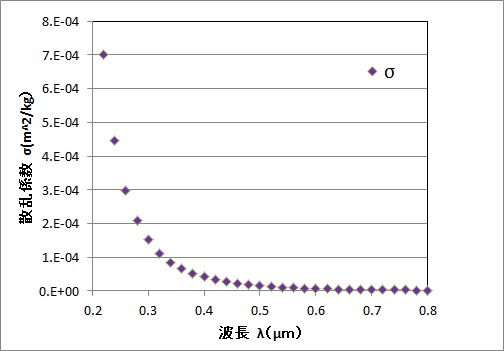
空気の屈折率(n-1)の波長依存性はEdlenの式を用いました。波長が大きくなると屈折率と散乱係数σRは減少します。
分子量Mwに対して、理想気体の状態方程式より
- ρ=MwP/RT=(Mw/RT)Po・exp[-z/H]=ρo・exp[-z/H]
- I=Io・exp{-σR∫ρdz}=Io・exp{-σRρoH }
となります。ここでHは高さパラメ-タで、大気の厚さH=8kmとしました。減光率は
- (Io-I)/Io=1-exp{-σRρH}
で求めました。減光率が小さいということは散乱され難いということです。
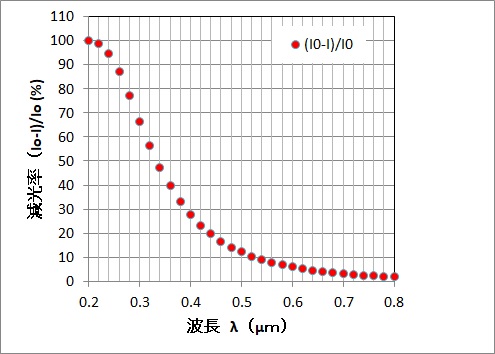
減光率は可視領域で波長が大きくなると、急速に減少します。近紫外領域(λ~0.3μm)では40%もの太陽光が失われます。青色光(λ~0.4μm)では30%、緑色光(λ~0.5μm)では12%、赤色光(λ~0.65μm)では4%、近赤外領域(λ~0.94μm)では1%しか失われません。様々な太陽高度と波長を考慮すると、大気に入射する平均太陽放射のうち13%がレイリ-散乱されているそうです。その半分が散乱光として地表面へ到達し、残り半分は宇宙空間へ放射されます。夕焼けのときは、8km以上の距離を太陽光が進むのでその間に青色光は殆ど散乱されてしまい、赤色光だけが届くことになります。

