＜双極子放射とは＞

　レ－リ－散乱のメカニズムについて古典力学的に考えましょう。太陽光は様々な波長の電磁波の集まりです。電磁波が空気分子の様な微小粒子に衝突すると向きが変わるのは何故でしょうか？

　それは電磁波が微小粒子に入射すると、粒子内で誘導分極が生じ、粒子から双極子放射が生じるからです。誘電分極とは、粒子に電場が掛かると、粒子の負電荷（電子）の中心と正電荷（原子核）の中心がずれて分極つまり電気双極子が誘導される現象です。電気双極子の大きさは正電荷と負電荷の間の距離ｒ(t)と電荷ｑの大きさの積です。

・　P(t)＝q・ｒ(t)

電気双極子の向きは、負電荷から正電荷の向きで、入射電場と常に平行です。粒子にかかる電場の向きや大きさが変化すれば、双極子の向きも大きさも変化します。電磁波では、電場が常に振動しているので、双極子も電場に合わせて振動します。振動する双極子から再び電磁波が放出されます。これが双極子放射です。

＜双極子放射がつくる電場＞

入射波の電場を

• E(t)=Eo・exp(iωt)

とおきます。ｔは時間、ωは角振動数です。ωは波数ｋとの間に

• ω＝cｋ

の分散関係があります。ここでc は光速です。波数は1ｍの中にある波の数です。波数ｋは波長λとの間に

• ｋ＝2π/λ

の関係があります。粒子内に生じる双極子ベクトルをP(t)とすると、

• P(t) =αε₀E(t)＝αε₀Eo・exp(ickt)

とかけます。αは粒子の分極率です。P(t)は振動すると周囲に電場を形成します。時刻ｔに双極子から距離ｒ離れた位置に観測される散乱波の電場をE(r,t)とすると、

• E(r,t) =(1/4πε₀)（1/ c²ｒ³）・ｒ×[ｒ×∂²P(t₀)/∂t₀²]

と書けます。×はベクトルの外積です。この公式は後で証明します。ここで、時刻t₀は双極子の加速振動が生じた時刻で、散乱波の観測時刻ｔとの間に

• t₀＝t－r/c

なる関係があります。つまり時刻t₀は時刻ｔよりr/c秒前の時刻です。ｒ方向の単位ベクトルeを導入すると、

• ｒ＝ｒe

と書けます。散乱光の電場は

• E(r,t) =(1/4πε₀)（1/ c²ｒ）・e×[e×∂²P(t－r/c)/∂t²]
• ＝(α/4π)（1/ c²ｒ）・e×[e×∂²｛Eo・exp[ick(t－r/c)]｝/∂t²]
• ＝－(α/4π)（ｋ²/ｒ）・e×[e×Eo ] ・exp[ick(t－r/c)]
• ＝El＋Er

となります。2回単位eベクトルと外積を取るので電場の向きは変わりません。

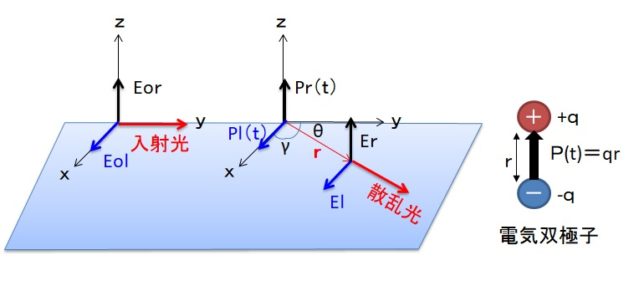
＜θ方向の散乱強度＞

いま入射電磁波はｙ方向に進行しており、電場Eoのｚ成分をEor、ｘ成分をEolと書くことにしましょう。

• Eo＝Eol＋Eor＝（Eol、0、Eor）

粒子の位置を原点として、散乱波の方向ｒはｘｙ平面内にあるものとします。ｘ軸と散乱波の方向ｒのなす角度をγと書きます。進行方向と散乱方向のなす角度をθ（＝π/2－γ）とします。

• e×[e×Eo ]＝e×[e×Eol ]＋e×[e×Eor ]＝A＋B

を計算します。AとBは直交しています。

• e＝（cosγ、sinγ、0　）、Eol＝Eol（1、0、0　）
• e×Eol ＝Eol（0、0、sinγ）、
• A =e×[e×Eol ]＝Eol（sinγsinγ、－sinγcosγ、0　）
• ∣A∣/ Eol =root[(sinγsinγ)²＋(－sinγcosγ)² ]＝sinγ＝sin（π/2－θ）＝cosθ

• e＝（cosγ、sinγ、0　）、Eor＝Eol（0、0、1　）
• e×Eol ＝Eol（sinγ、－cosγ、0）、
• Ｂ=e×[e×Eor ]＝Eol（0、0、－cosγcosγ－sinγsinγ）＝Eol（0、0、－1）
• ∣B∣/Eol =1

したがって、θ方向の散乱強度Iは

• I(θ)＝∣E(r,t) ∣²＝∣El∣²＋∣Er∣²
• ∣El∣²＝∣－（αｋ²/4πｒ）A exp[ick(t－r/c)]∣²＝(αｋ²/4πｒ)²・∣A∣²
• 　　　＝(αｋ²/4πｒ)²(cosθ)²・Eol²
• ∣Er∣²＝∣－（αｋ²/4πｒ）B・exp[ick(t－r/c)]∣²＝(αｋ²/4πｒ)²・∣B∣²
• 　　　＝(αｋ²/4πｒ)²・Eor²

両者を加えて、

• I(θ)＝(αｋ²/4πｒ)²(cosθ)²・Eol²＋(αｋ²/4πｒ)²・Eor²

となります。散乱体から離れると1/ｒ²で強度が減少します。散乱強度は波数の4乗に比例し、散乱の方向は等方的です。cosθの因子から分かるように、双極子ベクトルの方向には電場が形成されません。電場の水平成分Eolは進行方向に垂直な方向には散乱されませんが、前方と後方に等しく散乱されます。電場の垂直成分Eorは参照面内で等方的に散乱されます。粒子が大きくなるとミ－散乱となり、後方散乱は縮小し、前方散乱だけになります。ElとErの見かけの違いは、参照面をｘｙ面にしているために生じているものであって、ElとErの全体の散乱形状に違いはありません。

＜1粒子当たりの散乱断面積＞

ここで入射強度Ioに対し、入射電場強度は

• Io/2＝Eol²＝Eor²

を満たすとします。結局、θ方向の散乱強度として

・　I(θ)＝(αｋ²/4πｒ)² [(cosθ)²＋1]/2・Io

・　　＝(α/4πｒ)²・(2π/λ)⁴ [(cosθ)²＋1]/2・Io

が得られます。散乱強度が波長の4乗に反比例しています。全方向の散乱強度は

・　I＝∫dφ∫dθr²sinθ・I(θ）

・　＝Io・2π∫dθr²sinθ(α/4πｒ)²・(2π/λ)⁴ [(cosθ)²＋1]/2

・　＝Io 2π(2π/λ)⁴・(α/4π)²・(1/2)∫dθ[sinθ+ sinθ(cosθ)²]

・　＝Io 2π(2π/λ)⁴・(α/4π)²・(1/2)（2＋2/3）

・　＝Io 2π(2π/λ)⁴・(α/4π)²・(4/3）

結局、1粒子当たりの散乱断面積は

・　σ[m^2/個]＝I/Io＝128π⁵・(α/4π)²／3λ⁴

となります。

＜分極率と屈折率の関係＞

1個の分子の分極率は計測できないので、計測できる屈折率を用いて、分極率を表します。

単位体積当たりの分子数をNoとすると、分極率は

・　α＝（3/No）[(n²－1)/(n²＋2)]

と表せます。これについては後で説明します。δ＝n－1≒10^-4<<1ですから、δの2乗のオ－ダ－を無視すると

・　α≒（3/No）2(n－1)/3＝2(n－1)/No

と近似できます。n－1の波長や温度に対する依存性に関してはEdlenの実験式があります。

＜散乱断面積の換算＞

また1粒子当たりの散乱断面積に

・　No[個/m³]/ ρ_ｏ[kg/m³]＝No/ρ_ｏ[個/kg]

をかけて1kg当たりの散乱断面積に換算します。同時にαを代入すると

・　σ[m²/kg]＝σ[m²/個]・No/ρ_ｏ[個/kg]

・　＝128π⁵・[2(n－1)/No/4π]²／3λ⁴・No/ρ_ｏ

ですから、結局、1kg当たりの散乱断面積の公式

・　σ[m²/kg]＝32π³・[ｎ－1]^2／[ 3Noρ_ｏλ⁴]

が得られました。